Różne zadania z funkcji logarytmicznej
Poziom rozszerzony
Dana jest funkcja logarytmiczna o wzorze 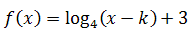 gdzie \(k\) jest parametrem. Dziedziną funkcji jest przedział \((2, +\infty )\). Podaj wartość parametru \(k\), a następnie:
gdzie \(k\) jest parametrem. Dziedziną funkcji jest przedział \((2, +\infty )\). Podaj wartość parametru \(k\), a następnie:
 Rozwiązanie PDF
Rozwiązanie PDF
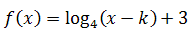 gdzie \(k\) jest parametrem. Dziedziną funkcji jest przedział \((2, +\infty )\). Podaj wartość parametru \(k\), a następnie:
gdzie \(k\) jest parametrem. Dziedziną funkcji jest przedział \((2, +\infty )\). Podaj wartość parametru \(k\), a następnie: - Oblicz wartość funkcji f dla argumentu 18.
- Oblicz argument dla którego wartość funkcji \(f\) wynosi \(3{,}5\).
- Określ dla jakich argumentów funkcja \(f\) przyjmuje wartości dodatnie.
 Rozwiązanie PDF
Rozwiązanie PDF Dana jest funkcja logarytmiczna o wzorze \(f(x)=\log_{\frac{2}{3}}(x-1)+p\) gdzie \(p\) jest parametrem. Wartość funkcji \(f\) dla argumentu \(x=3\frac{1}{4}\) wynosi \(3\). Oblicz wartość parametru \(p\), a następnie:  Rozwiązanie PDF
Rozwiązanie PDF
- Wyznacz argument dla którego wartość funkcji \(f\) wynosi \(6\).
- Wyznacz zbiór argumentów dla których funkcja \(f\) przyjmuje wartości mniejsze od \(1\).
 Rozwiązanie PDF
Rozwiązanie PDF Wyznacz wartości parametrów a i b we wzorze funkcji 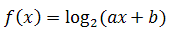 jeśli wiadomo, że punkty A = (1, 3) oraz B = (4, 5) należą do wykresu funkcji f. Wyznacz dziedzinę funkcji f.
jeśli wiadomo, że punkty A = (1, 3) oraz B = (4, 5) należą do wykresu funkcji f. Wyznacz dziedzinę funkcji f.
 Rozwiązanie PDF
Rozwiązanie PDF
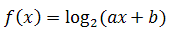 jeśli wiadomo, że punkty A = (1, 3) oraz B = (4, 5) należą do wykresu funkcji f. Wyznacz dziedzinę funkcji f.
jeśli wiadomo, że punkty A = (1, 3) oraz B = (4, 5) należą do wykresu funkcji f. Wyznacz dziedzinę funkcji f. Rozwiązanie PDF
Rozwiązanie PDF Funkcja \(f(x)\) dana jest poniższym wzorem: 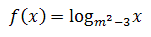 Dla jakiego parametru \(m\) funkcja jest malejąca?
Dla jakiego parametru \(m\) funkcja jest malejąca?  Rozwiązanie PDF
Rozwiązanie PDF
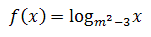 Dla jakiego parametru \(m\) funkcja jest malejąca?
Dla jakiego parametru \(m\) funkcja jest malejąca?  Rozwiązanie PDF
Rozwiązanie PDF Tematy nadrzędne i sąsiednie