Różne zadania z ciągu geometrycznego

Liczby \(2;\ 2x-1;\ 0{,}5\) (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem monotonicznego ciągu geometrycznego dla

Trzy lata temu pewne miasteczko liczyło \(25\ 000\) mieszkańców. Przez trzy ostatnie lata każdego roku liczba mieszkańców zmniejszyła się o \(10\%\). Oblicz, ile osób mieszka w tym miasteczku.

W ciągu geometrycznym \((a_n)\) dane są: \(a_1=36\), \(a_2=18\). Wtedy

Ciąg \((2\sqrt{2},4,a)\) jest geometryczny. Wówczas

W ciągu geometrycznym \((a_n)\) dane są: \(a_1 = 3\) i \(a_4 = 24\). Iloraz tego ciągu jest równy

Liczby \(2x, 16, x\) są trzema kolejnymi wyrazami ciągu geometrycznego. Oblicz \(x\).

Liczby \(12, 18, 2x + 1\) są, w podanej kolejności, odpowiednio pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wynika stąd, że

W ciągu geometrycznym \((a_n)\) dane są \(a_2=\frac{\sqrt{3}}{2}\) i \(a_3=-\frac{3}{2}\). Wtedy wyraz \(a_1\) jest równy

Liczby \(64, x, 4\) są odpowiednio pierwszym, drugim i trzecim wyrazem malejącego ciągu geometrycznego. Oblicz piąty wyraz tego ciągu.

Liczby \(-8,\ 4,\ x+1\) (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba \(x\) jest równa.

Dany jest nieskończony ciąg geometryczny \((a_n)\), w którym \(a_3=1\) i \(a_4=\frac{2}{3}\). Wtedy

Ciąg \((27, 18, x+5)\) jest geometryczny. Wtedy

Liczby \(3x−4\), \(8\), \(2\) w podanej kolejności są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wtedy

Ciąg \( (2x – 1, y, 6x + 3)\ \) jest arytmetyczny, a ciąg \( (3, y, 27)\ \) jest geometryczny rosnący. Oblicz \(x\) i \(y\).

Liczby: \( x-2,\ 6,\ 12 \), w podanej kolejności, są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba \( x \) jest równa

W ciągu geometrycznym \((a_n)\) pierwszy wyraz jest równy \(\frac{9}{8}\), a czwarty wyraz jest równy \(\frac{1}{3}\). Wówczas iloraz \(q\) tego ciągu jest równy

Nieskończony ciąg geometryczny \((a_n)\) jest określony wzorem \(a_n=7\cdot 3^{n+1}\), dla \(n\ge 1\). Oblicz iloraz \(q\) tego ciągu.

W dziewięciowyrazowym ciągu geometrycznym o wyrazach dodatnich pierwszy wyraz jest równy \(3\), a ostatni wyraz jest równy \(12\). Piąty wyraz tego ciągu jest równy

Kwadrat \(K_1\) ma bok długości \(a\). Obok niego rysujemy kolejno kwadraty \(K_2, K_3, K_4,...\) takie, że kolejny kwadrat ma bok połowę mniejszy od boku poprzedniego kwadratu (zobacz rysunek). 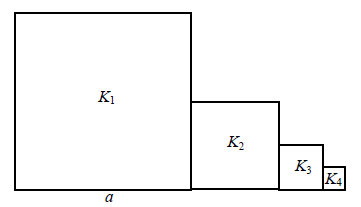Wyznacz pole kwadratu \(K_{12}\).

Dany jest ciąg geometryczny \((a_n)\), w którym pierwszy wyraz jest równy \(6\), a czwarty \(12\sqrt{2}\). Liczba \(\sqrt[3]{a_3-4}\) jest równa

Ciąg \((a_n)\) jest geometryczny oraz \(a_1=2\), \(a_2=6\). Liczby \(a_3, x, \frac{x}{2}\) w podanej kolejności tworzą ciąg arytmetyczny. Oblicz \(x\).

W rosnącym ciągu geometrycznym \((a_n)\), określonym dla \(n\ge 1\), spełniony jest warunek \(a_4=3a_1\). Iloraz \(q\) tego ciągu jest równy

W nieskończonym ciągu arytmetycznym \((a_n)\), określonym dla \(n\ge 1\), suma jedenastu początkowych wyrazów tego ciągu jest równa \(187\). Średnia arytmetyczna pierwszego, trzeciego i dziewiątego wyrazu tego ciągu, jest równa \(12\). Wyrazy \(a_1, a_3, a_k\) ciągu \((a_n)\), w podanej kolejności, tworzą nowy ciąg - trzywyrazowy ciąg geometryczny \((b_n)\). Oblicz \(k\).

Dany jest ciąg arytmetyczny \((a_n)\) o różnicy \(r \ne 0\) i pierwszym wyrazie \(a_1 = 2\). Pierwszy, drugi i czwarty wyraz tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Oblicz iloraz tego ciągu geometrycznego.

Wyznacz pierwszy wyraz i iloraz ciągu geometrycznego \((a_n)\), wiedząc, że:

Z beczki zawierającej \(30\) litrów wina karczmarz zaczerpnął \(1\) litr, a następnie dolał \(1\) litr wody. Postąpił tak dziesięć razy. Ile czystego wina pozostało w beczce?

Wykaż, że liczby \(\sqrt{5}-2,\ \frac{1}{2},\ \frac{\sqrt{5}+2}{4}\) tworzą ciąg geometryczny.

Wykaż, że liczby \(\frac{2+\sqrt{3}}{2-\sqrt{3}},\ \frac{2+\sqrt{3}}{2},\ \frac{1}{4}\) tworzą ciąg geometryczny.

Między liczby \(3\) i \(\frac{16}{2187}\) wstaw trzy liczby tak, by wraz z podanymi liczbami tworzyły ciąg geometryczny.

Między liczby \(12\) i \(2916\) wstaw cztery liczby tak, by wraz z podanymi liczbami tworzyły ciąg geometryczny.

Trzeci wyraz ciągu geometrycznego równa się \(45\), a szósty wynosi \(1215\). Znajdź sumę ośmiu pierwszych wyrazów tego ciągu.

Dwa wyrazy środkowe ciągu geometrycznego, mającego szesnaście wyrazów, równają się \(\frac{7}{3}\) i \(\frac{7}{9}\). Znajdź pierwszy wyraz i iloraz tego ciągu.

Ciąg geometryczny składa się z pięciu wyrazów, których suma wynosi \(124\). Iloraz sumy wyrazów skrajnych przez wyraz środkowy równy jest \(4{,}25\). Wyznacz ten ciąg.

Suma trzech wyrazów tworzących ciąg geometryczny jest równa \(21\), a ich iloczyn wynosi \(216\). Znajdź ten ciąg.

Wyznacz rosnący ciąg geometryczny, wiedząc, że suma wyrazów skrajnych jest równa \(34\), iloczyn tych wyrazów \(64\), a suma wszystkich wyrazów ciągu wynosi \(62\).

Znajdź ciąg geometryczny o czterech wyrazach, w którym wyraz trzeci zmniejszony o sumę dwóch pierwszych jest równy \(3\), a czwarty wyraz zmniejszony o sumę dwóch środkowych jest równy \(6\).

Wyznacz czterowyrazowy ciąg geometryczny, wiedząc, że iloczyn wyrazów skrajnych tego ciągu jest równy \(27\), a suma kwadratów dwóch pierwszych wyrazów wynosi \(10\).

Jaką jednakową liczbę należy dodać do każdej z liczb \(1, 10, 46,\) aby otrzymane sumy utworzyły ciąg geometryczny?

Za trzy książki, których ceny tworzą ciąg geometryczny, zapłacono \(61\) złotych. Za pierwszą i drugą razem zapłacono o \(11\) złotych więcej niż za trzecią. Ile zapłacono za każdą z książek?

Piłka odbijając się od ziemi osiągała za każdym razem wysokość wynoszącą \(\frac{2}{3}\) poprzedniej. Jak wysoko wzniosła się piłka po pierwszym uderzeniu, jeżeli po szóstym odbiła się na wysokość \(32\) cm?

Pan Jan złożył do banku \(2500\) zł na cztery lata na procent składany. Jaką kwotę będzie miał na koncie po tym okresie, jeżeli oprocentowanie w banku wynosi \(10\%\) w skali roku, a odsetki kapitalizuje się: Przy rozwiązaniu należy uwzględnić \(20\%\) podatek od odsetek.

Znajdź trzy liczby tworzące ciąg geometryczny, który ma własność: jeśli do drugiej liczby dodamy \(8\), ciąg zmieni się na arytmetyczny, jeśli do ostatniego wyrazu nowego ciągu dodamy \(64\), ciąg znów stanie się geometryczny.

Z czterech liczb trzy początkowe tworzą ciąg geometryczny, a trzy końcowe – ciąg arytmetyczny. Znajdź te liczby, jeśli suma liczb pierwszej i ostatniej równa się \(14\), suma drugiej i trzeciej \(12\).

Ciąg liczbowy \((a, b, c)\) jest arytmetyczny i \(a + b + c = 33\), natomiast ciąg \((a - 1, b + 5, c + 19)\) jest geometryczny. Oblicz \(a, b, c\).

Liczbę \(272\) przedstaw w postaci sumy czterech całkowitych składników tworzących ciąg geometryczny i takich, że trzeci składnik jest o \(48\) większy od pierwszego.