Reguła de l'Hospitala
Regułę l'Hospitala wykorzystuje się do liczenia granic wyrażeń nieoznaczonych.
Żeby stosować regułę l'Hospitala trzeba umieć liczyć pochodne.
Wówczas jeżeli: \[\lim_{x \to a} f(x) = \infty \quad \text{oraz}\quad \lim_{x \to a} g(x) = \infty\] lub \[\lim_{x \to a} f(x) = 0 \quad \text{oraz}\quad \lim_{x \to a} g(x) = 0\] to: \[\lim_{x \to a}\frac{f(x)}{g(x)}=\lim_{x \to a}\frac{f'(x)}{g'(x)}\] Powyższa równość zachodzi dodatkowo pod warunkiem, że granica po prawej stronie istnieje.
Punkt \(a\) może być konkretna liczbą, albo \(+\infty \) lub \(-\infty \).
Żeby stosować regułę l'Hospitala trzeba umieć liczyć pochodne.
Reguła de l'Hospitala
Załóżmy, że funkcje \(f(x)\) oraz \(g(x)\) są określone w otoczeniu punktu \(a\).Wówczas jeżeli: \[\lim_{x \to a} f(x) = \infty \quad \text{oraz}\quad \lim_{x \to a} g(x) = \infty\] lub \[\lim_{x \to a} f(x) = 0 \quad \text{oraz}\quad \lim_{x \to a} g(x) = 0\] to: \[\lim_{x \to a}\frac{f(x)}{g(x)}=\lim_{x \to a}\frac{f'(x)}{g'(x)}\] Powyższa równość zachodzi dodatkowo pod warunkiem, że granica po prawej stronie istnieje.
Punkt \(a\) może być konkretna liczbą, albo \(+\infty \) lub \(-\infty \).
W tym nagraniu wideo omawiam regułę de l'Hospitala
Oblicz granicę: \(\lim_{x \to 0} \frac{\sqrt[3]{1+x}-1}{x}\).
Oblicz granicę: \(\lim_{x \to 1} \frac{1-\sqrt[3]{x}}{1-\sqrt[5]{x}}\).
Oblicz granicę: \(\lim_{x \to 0}\frac{e^x-e^{-x}}{x} \)
Oblicz granicę \(\lim_{x \to 0} \frac{\cos px-\cos qx}{x^2}\), gdzie \(p,q\in \mathbb{R} \).
Oblicz granicę: \(\lim_{x \to 4}\frac{2-\sqrt{x}}{3-\sqrt{2x+1}} \)
Oblicz granicę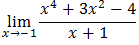 
.
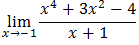.Oblicz granicę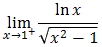 
.
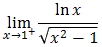.Oblicz granicę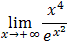 
.
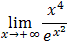.Oblicz granicę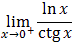 
.
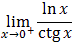.Oblicz granicę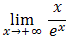 
.
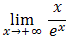.Oblicz granicę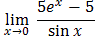 
.
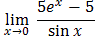.Oblicz granicę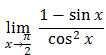 
.
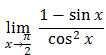.Oblicz granicę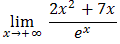 
.
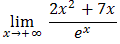.Oblicz granicę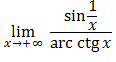 
.
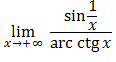.Oblicz granicę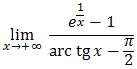 
.
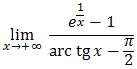.Oblicz granicę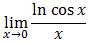 
.
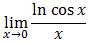.Oblicz granicę: \(\lim_{n \to \infty} \frac{(3^{n+1}+4^n)(n^2+n+3)}{(2^{2n}+3^n)(4^{n^2}-2)}\).