Pewniaki maturalne - formuła 2015
Poziom podstawowy
Poniżej prezentuje typy zadań najczęściej pojawiające się na maturze podstawowej z matematyki w formule 2015. Polecam również przerobić zadania treningowe od CKE
Wśród podanych przykładów znajdują się jedynie wybrane typy zadań. Pełną wiedzę niezbędną do zdania matury na 100% znajdziesz w kursie do matury podstawowej.
Typ I - zadania z potęg i pierwiastków
Na maturze bardzo często pojawiają się zadania sprawdzające umiejętność wykonywania działań na potęgach, pierwiastkach. Oto przykłady takich zadań:Zadanie 1. (1 pkt)
Liczba \(\frac{4^5\cdot 5^4}{20^4}\) jest równa
A.\( 4^4 \)
B.\( 20^{16} \)
C.\( 20^5 \)
D.\( 4 \)
Zadanie 2. (1 pkt)
Dla każdej dodatniej liczba \(a\) iloraz \(\frac{a^{-2{,}6}}{a^{1{,}3}}\) jest równy
A.\( a^{-3{,}9} \)
B.\( a^{-2} \)
C.\( a^{-1{,}3} \)
D.\( a^{1{,}3} \)
Zadanie 3. (1 pkt)
Liczba \(\frac{9^5\cdot 5^9}{45^5}\) jest równa
A.\( 45^{40} \)
B.\( 45^9 \)
C.\( 9^4 \)
D.\( 5^4 \)
Zadanie 4. (1 pkt)
Liczba \(\sqrt{\frac{9}{7}}+\sqrt{\frac{7}{9}}\) jest równa
A.\( \sqrt{\frac{16}{63}} \)
B.\( \frac{16}{3\sqrt{7}} \)
C.\( 1 \)
D.\( \frac{3+\sqrt{7}}{3\sqrt{7}} \)
Typ II - procenty
Równie często na maturze podstawowej pojawiają się zadania z procentów (zazwyczaj jest jedno takie zadanie za 1 punkt) tego typu:Zadanie 5. (1 pkt)
Liczby \(a\) i \(c\) są dodatnie. Liczba \(b\) stanowi \(48\%\) liczby \(a\) oraz \(32\%\) liczby \(c\). Wynika stąd, że
A.\( c=1{,}5a \)
B.\( c=1{,}6a \)
C.\( c=0{,}8a \)
D.\( c=0{,}16a \)
Zadanie 6. (1 pkt)
Buty, które kosztowały \(220\) złotych, przeceniono i sprzedano za \(176\) złotych. O ile procent obniżono cenę butów?
A.\( 80 \)
B.\( 20 \)
C.\( 22 \)
D.\( 44 \)
Zadanie 7. (1 pkt)
Dany jest prostokąt o wymiarach \(40 \text{ cm} \times 100 \text{ cm}\). Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o \(20\%\), a każdy z krótszych boków skrócimy o \(20\%\), to w wyniku obu przekształceń pole tego prostokąta
A.zwiększy się o \( 8\% \)
B.zwiększy się o \( 4\% \)
C.zmniejszy się o \( 8\% \)
D.zmniejszy się o \( 4\% \)
Zadanie 8. (1 pkt)
Kwotę \(1000\) zł ulokowano w banku na roczną lokatę oprocentowaną w wysokości \(4\%\) w stosunku rocznym. Po zakończeniu lokaty od naliczonych odsetek odprowadzany jest podatek w wysokości \(19\%\). Maksymalna kwota, jaką po upływie roku będzie można wypłacić z banku, jest równa
A.\( 1000\cdot \left ( 1+\frac{81}{100}\cdot \frac{4}{100} \right ) \)
B.\( 1000\cdot \left ( 1-\frac{19}{100}\cdot \frac{4}{100} \right ) \)
C.\( 1000\cdot \left ( 1-\frac{81}{100}\cdot \frac{4}{100} \right ) \)
D.\( 1000\cdot \left ( 1+\frac{19}{100}\cdot \frac{4}{100} \right ) \)
Typ III - logarytmy
Na maturze praktycznie zawsze pojawia się przynajmniej jedno zadanie na liczenie logarytmów. Oto przykładowe zadania:Zadanie 9. (1 pkt)
Liczba \(\log_{\sqrt{2}}(2\sqrt{2})\) jest równa
A.\( \frac{3}{2} \)
B.\( 2 \)
C.\( \frac{5}{2} \)
D.\( 3 \)
Zadanie 10. (1 pkt)
Liczba \(\frac{\log_3729}{\log_636}\) jest równa
A.\( \log_6693 \)
B.\( 3 \)
C.\( \log_{\frac{1}{2}}\frac{81}{4} \)
D.\( 4 \)
Zadanie 11. (1 pkt)
Dane są liczby \(a=-\frac{1}{27}\), \(b=\log_{\frac{1}{4}}64\), \(c=\log_{\frac{1}{3}}27\). Iloczyn \(abc\) jest równy
A.\( 3 \)
B.\( \frac{1}{3} \)
C.\( -\frac{1}{3} \)
D.\( -9 \)
Zadanie 12. (1 pkt)
Wartość wyrażenia \(\log_50{,}04-\frac{1}{2}\log_{25}1\) jest równa
A.\( -3 \)
B.\( -2\frac{1}{4} \)
C.\( -2 \)
D.\( 0 \)
Typ IV - równania i nierówności liniowe oraz funkcja liniowa
Jednym z ważniejszych pojęć na maturze podstawowej jest funkcja liniowa i związane z nią równania oraz nierówności. Zazwyczaj z tego zagadnienia pojawia się na maturze od 2 do 5 zadań. Z funkcji liniowych szczególnie często zdarzają się zdania sprawdzające umiejętność liczenia miejsc zerowych, oraz badanie równoległości i prostopadłości prostych.Zadanie 13. (1 pkt)
Równanie \(\frac{x-1}{x+1}=x-1\)
A.ma dokładnie dwa rozwiązania \( x=0 \), \(x=1\)
B.ma dokładnie jedno rozwiązanie \( x=-1 \)
C.ma dokładnie jedno rozwiązanie \( x=0 \)
D.ma dokładnie jedno rozwiązanie \( x=1 \)
Zadanie 14. (1 pkt)
Równanie wymierne \(\frac{3x-1}{x+5}=3\), gdzie \(x\ne -5\),
A.nie ma rozwiązań rzeczywistych.
B.ma dokładnie jedno rozwiązanie rzeczywiste.
C.ma dokładnie dwa rozwiązania rzeczywiste.
D.ma dokładnie trzy rozwiązania rzeczywiste.
Zadanie 15. (1 pkt)
Najmniejszą liczbą całkowitą spełniającą nierówność \(\frac{x}{5}+\sqrt{7}\gt 0\) jest
A.\( -14 \)
B.\( -13 \)
C.\( 13 \)
D.\( 14 \)
Zadanie 16. (1 pkt)
Najmniejszą liczbą całkowitą spełniającą nierówność \(2(x − 2) \le 4(x −1)+1\) jest
A.\( -2 \)
B.\( -1 \)
C.\( 0 \)
D.\( 1 \)
Zadanie 17. (1 pkt)
Równość \(\frac{m}{5-\sqrt{5}}=\frac{5+\sqrt{5}}{5}\) zachodzi dla
A.\( m=-5 \)
B.\( m=1 \)
C.\( m=4 \)
D.\( m=5 \)
Zadanie 18. (1 pkt)
Dana jest funkcja liniowa \(f(x)=\frac{3}{4}x+6\). Miejscem zerowym tej funkcji jest liczba
A.\( 8 \)
B.\( 6 \)
C.\( -6 \)
D.\( -8 \)
Zadanie 19. (1 pkt)
Funkcja liniowa \(f\) określona wzorem \(f(x)=2x+b\) ma takie samo miejsce zerowe, jakie ma funkcja \(g(x)=-3x+4\). Stąd wynika, że
A.\( b=-\frac{8}{3} \)
B.\( b=\frac{4}{3} \)
C.\( b=4 \)
D.\( b=-\frac{3}{2} \)
Zadanie 20. (1 pkt)
Wykres funkcji liniowej \(y = 2x − 3\) przecina oś \(Oy\) w punkcie o współrzędnych
A.\( (0,-3) \)
B.\( (-3,0) \)
C.\( (0,2) \)
D.\( (0,3) \)
Zadanie 21. (1 pkt)
Prosta \(l\) o równaniu \(y=m^2x+3\) jest równoległa do prostej \(k\) o równaniu \(y=(4m-4)x-3\). Zatem:
A.\( m=2 \)
B.\( m=-2 \)
C.\( m=-2-2\sqrt{2} \)
D.\( m=2+2\sqrt{2} \)
Zadanie 22. (1 pkt)
Proste o równaniach: \(y=2mx-m^2-1\) oraz \(y=4m^2x+m^2+1\) są prostopadłe dla
A.\( m=-\frac{1}{2} \)
B.\( m=\frac{1}{2} \)
C.\( m=1 \)
D.\( m=2 \)
Zadanie 23. (1 pkt)
Proste opisane równaniami \(y=\frac{2}{m-1}x+m-2\) oraz \(y=mx+\frac{1}{m+1}\) są prostopadłe, gdy
A.\( m=2 \)
B.\( m=\frac{1}{2} \)
C.\( m=\frac{1}{3} \)
D.\( m=-2 \)
Typ V - równania i nierówności kwadratowe oraz funkcja kwadratowa
Zadania związane z funkcją kwadratową, to na każdej maturze punkt obowiązkowy. Musimy umieć znajdować miejsca zerowe funkcji kwadratowej (czyli rozwiązywać równania kwadratowe), wierzchołek oraz zapisywać w różnych postaciach funkcję kwadratową (ogólna, iloczynowa i kanoniczna). Musimy również umieć rysować wykresy funkcji kwadratowej, co szczególnie przydaje się podczas rozwiązywania nierówności kwadratowych (praktycznie zawsze pojawia się na maturze takie zadanie za 2 punkty). Często również pojawiają się zadania na znajdowanie wartości ekstremalnych funkcji kwadratowych na przedziałach domkniętych. Dokładniejsze omówienie tych wszystkich zagadnień znajdziesz w kursie do matury podstawowej (części: 14-15 oraz 26-30), a poniżej przykładowe, najczęstsze typy zadań:Zadanie 24. (1 pkt)
Równość \((2\sqrt{2}-a)^2=17-12\sqrt{2}\) jest prawdziwa dla
A.\( a=3 \)
B.\( a=1 \)
C.\( a=-2 \)
D.\( a=-3 \)
Zadanie 25. (2 pkt)
Oblicz najmniejszą i największą wartość funkcji kwadratowej \(f(x)=x^2-6x+3\) w przedziale \(\langle 0,4\rangle \).
Zadanie 26. (2 pkt)
Rozwiąż nierówność \(2x^2-4x\gt (x+3)(x-2)\).
Zadanie 27. (2 pkt)
Rozwiąż nierówność \(2x^2-4x\gt 3x^2-6x\).
Zadanie 28. (2 pkt)
Rozwiąż nierówność \(20x \ge 4x^2 + 24\).
Zadanie 29. (2 pkt)
Rozwiąż nierówność \(3x^2-6x\ge (x-2)(x-8)\)
Zadanie 30. (5 pkt)
Funkcja kwadratowa \(f\) określona jest wzorem \(f(x) = ax^2 + bx + c\). Zbiorem rozwiązań nierówności \(f(x) \gt 0\) jest przedział \((0,12)\). Największa wartość funkcji \(f\) jest równa \(9\). Oblicz współczynniki \(a\), \(b\) i \(c\) funkcji \(f\).
Zadanie 31. (1 pkt)
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej \(f\). Wierzchołkiem tej paraboli jest punkt \(W=(1,9)\). Liczby \(-2\) i \(4\) to miejsca zerowe funkcji \(f\).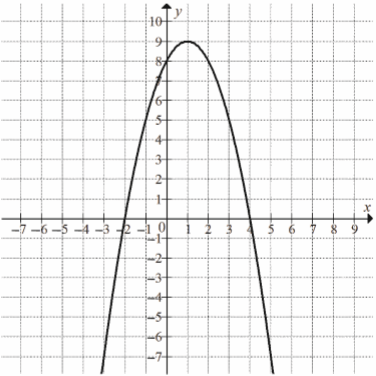 
Najmniejsza wartość funkcji \(f\) w przedziale \(\langle -1;2 \rangle \) jest równa
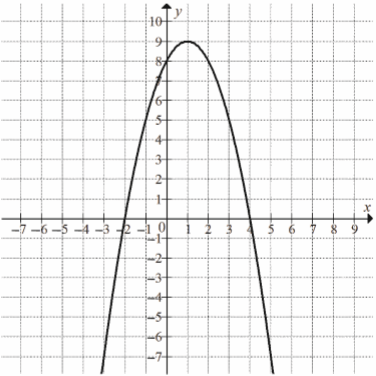Najmniejsza wartość funkcji \(f\) w przedziale \(\langle -1;2 \rangle \) jest równa A.\( 2 \)
B.\( 5 \)
C.\( 8 \)
D.\( 9 \)
Zadanie 32. (1 pkt)
Jeśli funkcja kwadratowa \(f(x)=x^2+2x+3a\) nie ma ani jednego miejsca zerowego, to liczba \(a\) spełnia warunek
A.\( a\lt -1 \)
B.\( -1\le a\lt 0 \)
C.\( 0\le a\lt \frac{1}{3} \)
D.\( a\gt \frac{1}{3} \)
Zadanie 33. (2 pkt)
Funkcja kwadratowa jest określona wzorem \(f(x)=x^2-11x\). Oblicz najmniejszą wartość funkcji \(f\) w przedziale \(\langle -6,6\rangle \).
Typ VI - różne zadania z funkcji
Częstym na maturze zdarza się zadanie, w którym należy wyznaczyć zbiór wartości funkcji danej na wykresie, lub odgadnąć przesunięcie. Oto przykładowe takie zadania:Zadanie 34. (1 pkt)
Na rysunku przedstawiono wykres funkcji \(f\).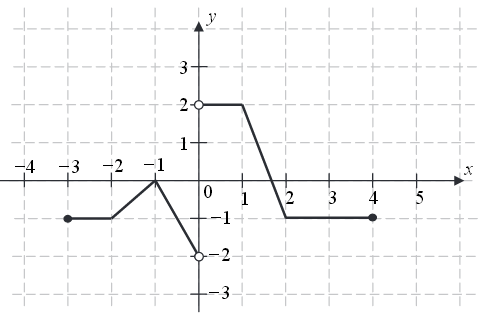 
Zbiorem wartości funkcji \(f\) jest
Zbiorem wartości funkcji \(f\) jest A.\( (-2,2\rangle \)
B.\( \langle -2,2\rangle \)
C.\( \langle -2,2) \)
D.\( (-2,2) \)
Zadanie 35. (1 pkt)
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej \(f\). Wierzchołkiem tej paraboli jest punkt \(W=(1,9)\). Liczby \(-2\) i \(4\) to miejsca zerowe funkcji \(f\). 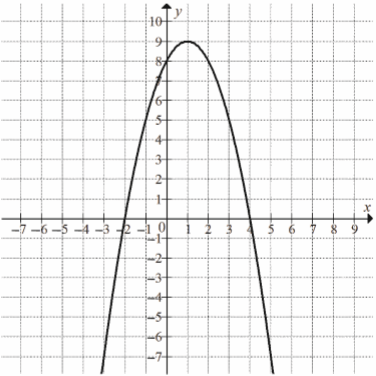Zbiorem wartości funkcji \(f\) jest przedział
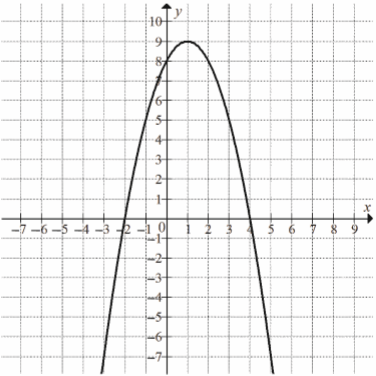Zbiorem wartości funkcji \(f\) jest przedział A.\( (-\infty ;-2\rangle \)
B.\( \langle -2;4 \rangle \)
C.\( \langle 4;+\infty ) \)
D.\( (-\infty ;9\rangle \)
Zadanie 36. (1 pkt)
Gdy przesuniemy wykres funkcji \(f(x)=2x-3\) o \(2\) jednostki w prawo i \(4\) jednostki w górę, to otrzymamy wykres funkcji opisanej wzorem
A.\( y=2(x-2)+4 \)
B.\( y=2(x-2)-4 \)
C.\( y=2(x-2)+1 \)
D.\( y=2(x+2)+4 \)
Zadanie 37. (1 pkt)
Funkcja \(g\) jest określona wzorem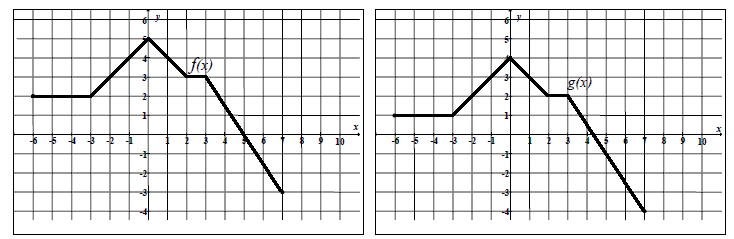 
A.\( g(x)=f(x-1) \)
B.\( g(x)=f(x)-1 \)
C.\( g(x)=f(x+1) \)
D.\( g(x)=f(x)+1 \)
Typ VII - układy równań
Często na maturze jest jedno zadanie z układu równań następujących typów:Zadanie 38. (1 pkt)
Układ równań \(\begin{cases} 2x-3y=5 \\ -4x+6y=-10 \end{cases} \)
A.nie ma rozwiązań.
B.ma dokładnie jedno rozwiązanie.
C.ma dokładnie dwa rozwiązania.
D.ma nieskończenie wiele rozwiązań.
Zadanie 39. (1 pkt)
Układ równań \(\begin{cases} x-y=3 \\ 2x+0{,}5y=4 \end{cases} \) opisuje w układzie współrzędnych na płaszczyźnie
A.zbiór nieskończony.
B.dokładnie 2 różne punkty.
C.dokładnie jeden punkt.
D.zbiór pusty.
Typ VIII - wartość bezwzględna i błędy
Czasami na maturze jest jedno zadanie z wartości bezwzględnej lub błędów względnych i bezwzględnych. Oto przykładowe zadania jakie mogą się pojawić:Zadanie 40. (1 pkt)
Liczba \(\frac{|3-9|}{-3}\) jest równa
A.\( 2 \)
B.\( -2 \)
C.\( 0 \)
D.\( -4 \)
Zadanie 41. (2 pkt)
W tabeli przedstawiono roczne przyrosty wysokości pewnej sosny w ciągu sześciu kolejnych lat.
Oblicz średni roczny przyrost wysokości tej sosny w badanym okresie sześciu lat. Otrzymany wynik zaokrąglij do \(1\) cm. Oblicz błąd względny otrzymanego przybliżenia. Podaj ten błąd w procentach.
| kolejne lata | 1 | 2 | 3 | 4 | 5 | 6 |
| przyrost (w cm) | 10 | 10 | 7 | 8 | 8 | 7 |
Typ IX - trygonometria
Zadania z trygonometrii pojawiają się a każdej maturze podstawowej. Oto najczęstsze typy:Zadanie 42. (1 pkt)
Kąt \(\alpha \) jest ostry i \(\operatorname{tg} \alpha =\frac{2}{3}\). Wtedy
A.\( \sin \alpha =\frac{3\sqrt{13}}{26} \)
B.\( \sin \alpha =\frac{\sqrt{13}}{13} \)
C.\( \sin \alpha =\frac{2\sqrt{13}}{13} \)
D.\( \sin \alpha =\frac{3\sqrt{13}}{13} \)
Zadanie 43. (1 pkt)
Liczba \( \sin 150^\circ \) jest równa liczbie
A.\( \cos 60^\circ \)
B.\( \cos 120^\circ \)
C.\( \operatorname{tg} 120^\circ \)
D.\( \operatorname{tg} 60^\circ \)
Zadanie 44. (1 pkt)
Dany jest trójkąt prostokątny o kątach ostrych \(\alpha \) i \(\beta \), w którym \(\sin \alpha = \frac{\sqrt{6}}{3}\). Wtedy
A.\( \cos \alpha =\frac{\sqrt{3}}{2} \)
B.\( \cos \beta =\frac{\sqrt{6}}{3} \)
C.\( \operatorname{tg} \alpha =\frac{\sqrt{3}}{3} \)
D.\( \operatorname{tg} \beta =\frac{\sqrt{6}}{2} \)
Zadanie 45. (2 pkt)
Dana jest liczba \(a=\sin 72^\circ \). Zapisz liczbę \(1+\operatorname{tg}^2 72^\circ \) w zależności od \(a\).
Zadanie 46. (1 pkt)
Wartość wyrażenia \((\operatorname{tg} 60^\circ +\operatorname{tg} 45^\circ )^2-\sin 60^\circ \) jest równa
A.\( 2-\frac{3\sqrt{3}}{2} \)
B.\( 2+\frac{\sqrt{3}}{2} \)
C.\( 4-\frac{\sqrt{3}}{2} \)
D.\( 4+\frac{3\sqrt{3}}{2} \)
Zadanie 47. (1 pkt)
W układzie współrzędnych zaznaczono kąt \(\alpha \).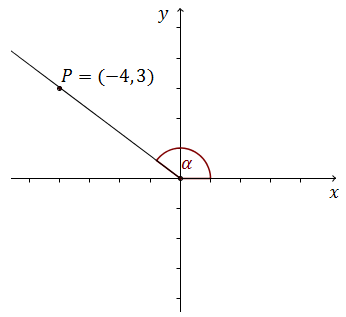 
Jedno z ramion kąta \(\alpha \) przechodzi przez punkt \(P=(-4,3)\). Wtedy:
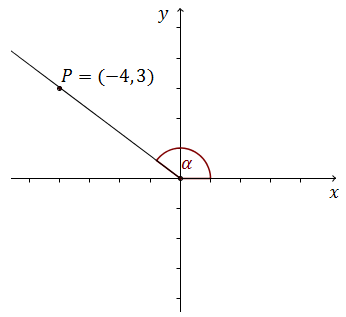Jedno z ramion kąta \(\alpha \) przechodzi przez punkt \(P=(-4,3)\). Wtedy: A.\( \cos \alpha = \frac{4}{5} \)
B.\( \cos \alpha = -\frac{4}{5} \)
C.\( \cos \alpha = -\frac{4}{3} \)
D.\( \cos \alpha = -\frac{3}{4} \)
Typ X - ciąg arytmetyczny i geometryczny
Zadania z ciągów zawsze pojawiają się na maturze. Zawsze są przynajmniej dwa zadania z tego zagadnienia. Poniżej prezentuję najczęstsze typy zadań z ciągów:Zadanie 48. (1 pkt)
Czternasty wyraz ciągu arytmetycznego jest równy \(8\), a różnica tego ciągu jest równa \(\left (-\frac{3}{2}\right )\). Siódmy wyraz tego ciągu jest równy
A.\( \frac{37}{2} \)
B.\( -\frac{37}{2} \)
C.\( -\frac{5}{2} \)
D.\( \frac{5}{2} \)
Zadanie 49. (1 pkt)
Wszystkie dwucyfrowe liczby naturalne podzielne przez \(7\) tworzą rosnący ciąg arytmetyczny. Dwunastym wyrazem tego ciągu jest liczba
A.\( 77 \)
B.\( 84 \)
C.\( 91 \)
D.\( 98 \)
Zadanie 50. (1 pkt)
W rosnącym ciągu geometrycznym \((a_n)\), określonym dla \(n\ge 1\), spełniony jest warunek \(a_4=3a_1\). Iloraz \(q\) tego ciągu jest równy
A.\( q=\frac{1}{\sqrt[3]{3}} \)
B.\( q=\frac{1}{3} \)
C.\( q=3 \)
D.\( q=\sqrt[3]{3} \)
Zadanie 51. (1 pkt)
Trójwyrazowy ciąg \((x+1,x-1,2x)\) jest arytmetyczny dla
A.\( x=-3 \)
B.\( x=-1 \)
C.\( x=0 \)
D.\( x=2 \)
Zadanie 52. (1 pkt)
Ciąg \((x,2x+3,4x+3)\) jest geometryczny. Pierwszy wyraz tego ciągu jest równy
A.\( -4 \)
B.\( 1 \)
C.\( 0 \)
D.\( -1 \)
Typ XI - geometria płaska
W geometrii najczęściej przydaje się nam twierdzenie Pitagorasa i musimy je umieć stosować na blachę (jest ono również bardzo przydatne w geometrii przestrzennej). Zadania z geometrii zazwyczaj nie są szablonowe, więc trudno tu podać konkretne typy jako pewniaki. Na pewno można wyróżnić zadania z kątami wpisanymi i środkowymi w okręgu - często się pojawiają na maturze. Także często pojawia się podobieństwo trójkątów.Zadanie 53. (1 pkt)
Punkty \(A\), \(B\), \(C\) i \(D\) leżą na okręgu o środku \(S\). Cięciwa \(CD\) przecina średnicę \(AB\) tego okręgu w punkcie \(E\) tak, że \(|\sphericalangle BEC|=100^\circ \). Kąt środkowy \(ASC\) ma miarę \(110^\circ \) (zobacz rysunek). 
Kąt wpisany \(BAD\) ma miarę
Kąt wpisany \(BAD\) ma miarę A.\( 15^\circ \)
B.\( 20^\circ \)
C.\( 25^\circ \)
D.\( 30^\circ \)
Zadanie 54. (1 pkt)
W okręgu o środku \(O\) dany jest kąt o mierze \(50^\circ \), zaznaczony na rysunku.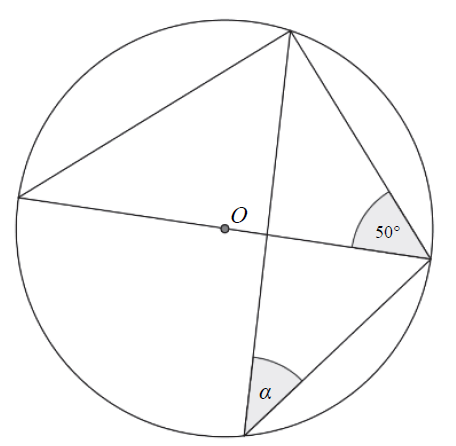 
Miara kąta oznaczonego na rysunku literą \(\alpha \) jest równa
Miara kąta oznaczonego na rysunku literą \(\alpha \) jest równa A.\( 40^\circ \)
B.\( 50^\circ \)
C.\( 20^\circ \)
D.\( 25^\circ \)
Zadanie 55. (1 pkt)
Przedstawione na rysunku trójkąty \(ABC\) i \(PQR\) są podobne. Bok \(AB\) trójkąta \(ABC\) ma długość 
A.\( 8 \)
B.\( 8{,}5 \)
C.\( 9{,}5 \)
D.\( 10 \)
Zadanie 56. (1 pkt)
Okręgi o promieniach \(3\) i \(4\) są styczne zewnętrznie. Prosta styczna do okręgu o promieniu \(4\) w punkcie \(P\) przechodzi przez środek okręgu o promieniu \(3\) (zobacz rysunek). 
Pole trójkąta, którego wierzchołkami są środki okręgów i punkt styczności \(P\), jest równe
Pole trójkąta, którego wierzchołkami są środki okręgów i punkt styczności \(P\), jest równe A.\( 14 \)
B.\( 2\sqrt{33} \)
C.\( 4\sqrt{33} \)
D.\( 12 \)
Typ XII - geometria przestrzenna
Zadania ze stereometrii często pojawiają się za większa liczbę punktów.Zadanie 57. (1 pkt)
Przekątna podstawy graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek). 
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt \(\alpha \) o mierze
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt \(\alpha \) o mierze A.\( 30^\circ \)
B.\( 45^\circ \)
C.\( 60^\circ \)
D.\( 75^\circ \)
Zadanie 58. (4 pkt)
Wysokość graniastosłupa prawidłowego czworokątnego jest równa \(16\). Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego cosinus jest równy \(\frac{3}{5}\). Oblicz pole powierzchni całkowitej tego graniastosłupa.
Zadanie 59. (4 pkt)
Podstawą ostrosłupa \(ABCDS\) jest prostokąt, którego boki pozostają w stosunku \(3 : 4\), a pole jest równe \(192\) (zobacz rysunek). Punkt \(E\) jest wyznaczony przez przecinające się przekątne podstawy, a odcinek \(SE\) jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem \(30^\circ\). Oblicz objętość ostrosłupa.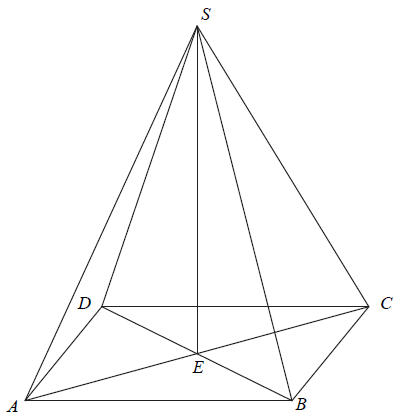 
Zadanie 60. (1 pkt)
Kąt rozwarcia stożka ma miarę \(120^\circ \), a tworząca tego stożka ma długość \(4\). Objętość tego stożka jest równa
A.\( 36\pi \)
B.\( 18\pi \)
C.\( 24\pi \)
D.\( 8\pi \)
Zadanie 61. (5 pkt)
Trójkąt równoboczny \(ABC\) jest podstawą ostrosłupa prawidłowego \(ABCS\), w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem \(60^\circ \), a krawędź boczna ma długość \(7\) (zobacz rysunek). Oblicz objętość tego ostrosłupa. 
Typ XIII - geometria analityczna
Z geometrii analitycznej na pewno musimy umieć liczyć długość odcinka, wyznaczać równania prostych przechodzących przez dwa punkty, a także równoległych i prostopadłych, wyznaczać środek odcinka. Oto przykładowe zadania z tych zagadnień:Zadanie 62. (1 pkt)
W układzie współrzędnych dane są punkty \(A=(a,6)\) oraz \(B=(7,b)\). Środkiem odcinka \(AB\) jest punkt \(M=(3,4)\). Wynika stąd, że
A.\( a=5 \) i \(b=5\)
B.\( a=-1 \) i \(b=2\)
C.\( a=4 \) i \(b=10\)
D.\( a=-4 \) i \(b=-2\)
Zadanie 63. (1 pkt)
Na rysunku jest przedstawiona prosta zawierająca przekątną \(AC\) rombu \(ABCD\) oraz wierzchołki \(A=(-2,1)\) i \(C=(4,5)\) tego rombu.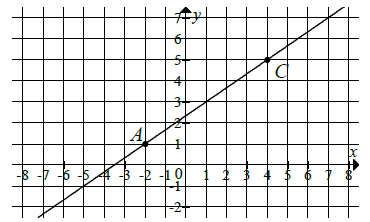 
Wskaż równanie prostej zawierającej przekątną \(BD\) tego rombu.
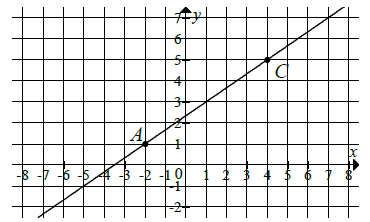Wskaż równanie prostej zawierającej przekątną \(BD\) tego rombu. A.\( y=-\frac{2}{3}x+\frac{11}{3} \)
B.\( y=-\frac{3}{2}x+4 \)
C.\( y=-x+4 \)
D.\( y=-\frac{3}{2}x+\frac{9}{2} \)
Zadanie 64. (1 pkt)
Okręgi o środkach \(S_1=(3,4)\) oraz \(S_2=(9,-4)\) i równych promieniach są styczne zewnętrznie. Promień każdego z tych okręgów jest równy
A.\( 8 \)
B.\( 6 \)
C.\( 5 \)
D.\( \frac{5}{2} \)
Zadanie 65. (2 pkt)
W układzie współrzędnych dane są punkty \(A=(-43,-12)\), \(B=(50,19)\). Prosta \(AB\) przecina oś \(Ox\) w punkcie \(P\). Oblicz pierwszą współrzędną punktu \(P\).
Typ XIV - statystyka i rachunek prawdopodobieństwa
Ze statystyki najczęściej pojawiają się zadania związane ze średnią arytmetyczną i medianą. Zadania z kombinatoryki i rachunku prawdopodobieństwa zawsze opierają się na regule mnożenia i dodawania (zadani z kostkami i monetami, losowanie kul lub liczb ze zbioru).Zadanie 66. (1 pkt)
Jeżeli do zestawu czterech danych: \(4, 7, 8, x\) dołączymy liczbę \(2\), to średnia arytmetyczna wzrośnie o \(2\). Zatem
A.\( x=-51 \)
B.\( x=-6 \)
C.\( x=10 \)
D.\( x=29 \)
Zadanie 67. (1 pkt)
Średnia arytmetyczna zestawu danych: \[2,4,7,8,9\] jest taka sama jak średnia arytmetyczna zestawu danych: \[2,4,7,8,9,x.\] Wynika stąd, że
A.\( x=3 \)
B.\( x=5 \)
C.\( x=6 \)
D.\( x=0 \)
Zadanie 68. (1 pkt)
Średnia arytmetyczna sześciu liczb naturalnych: \(31, 16, 25, 29, 27, x\), jest równa \(\frac{x}{2}\). Mediana tych liczb jest równa
A.\( 26 \)
B.\( 27 \)
C.\( 28 \)
D.\( 29 \)
Zadanie 69. (1 pkt)
W każdym z trzech pojemników znajduje się para kul, z których jedna jest czerwona, a druga - niebieska. Z każdego pojemnika losujemy jedną kulę. Niech \(p\) oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z trzech wylosowanych kul będą czerwone. Wtedy
A.\( p=\frac{3}{8} \)
B.\( p=\frac{1}{4} \)
C.\( p=\frac{2}{3} \)
D.\( p=\frac{1}{2} \)
Zadanie 70. (1 pkt)
Rzucamy trzy razy symetryczną monetą. Niech \(p\) oznacza prawdopodobieństwo otrzymania dokładnie dwóch orłów w tych trzech rzutach. Wtedy
A.\( 0\le p\le 0{,}2 \)
B.\( 0{,}2\le p\le 0{,}35 \)
C.\( 0{,}35\lt p\le 0{,}5 \)
D.\( 0{,}5\lt p\le 1 \)
Zadanie 71. (1 pkt)
Ile jest wszystkich dwucyfrowych liczb naturalnych podzielnych przez \(3\)?
A.\( 12 \)
B.\( 24 \)
C.\( 29 \)
D.\( 30 \)
Zadanie 72. (2 pkt)
Ze zbioru siedmiu liczb naturalnych \(\{1, 2, 3, 4, 5, 6, 7\}\) losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że większą z wylosowanych liczb będzie liczba \(5\).
Pewniaki na STARĄ podstawę programową
Poniżej prezentuję pewniaki do "starej" podstawy programowej.Zadanie 73. (1 pkt)
Cena towaru bez podatku VAT jest równa \(60\) zł. Towar ten wraz z podatkiem VAT w wysokości \(22\%\) kosztuje
A.\( 73{,}20 \) zł
B.\( 49{,}18 \) zł
C.\( 60{,}22 \) zł
D.\( 82 \) zł
Zadanie 74. (1 pkt)
Samochód kosztował \(30000\) zł. Jego cenę obniżono o \(10\%\), a następnie cenę po tej obniżce ponownie obniżono o \(10\%\). Po tych obniżkach samochód kosztował
A.\( 24400 \) zł
B.\( 24700 \) zł
C.\( 24000 \) zł
D.\( 24300 \) zł
Zadanie 75. (1 pkt)
Iloczyn \(\ 81^2\cdot 9^4\ \) jest równy
A.\( 3^4 \)
B.\( 3^0 \)
C.\( 3^{16} \)
D.\( 3^{14} \)
Zadanie 76. (1 pkt)
Różnica \(\ \log_{3}9-\log_{3}1\ \) jest równa
A.\( 0 \)
B.\( 1 \)
C.\( 2 \)
D.\( 3 \)
Zadanie 77. (1 pkt)
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej. 
A.\( |x-1| \lt 3 \)
B.\( |x+1| \lt 3 \)
C.\( |x+1| > 3 \)
D.\( |x-1| > 3 \)
Zadanie 78. (1 pkt)
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności \(|x-2| \ge 3\).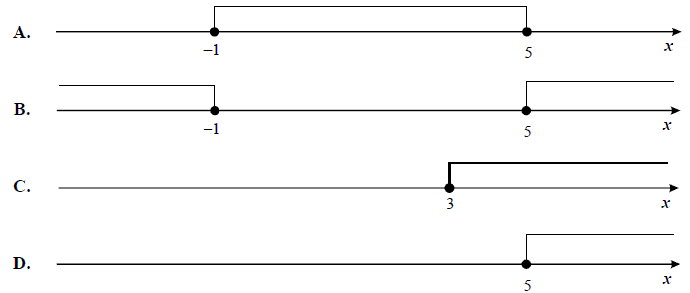 
Zadanie 79. (1 pkt)
Kwadrat liczby \(\ x=5+2\sqrt{3}\ \) jest równy
A.\( 37 \)
B.\( 25+4\sqrt{3} \)
C.\( 37+20\sqrt{3} \)
D.\( 147 \)
Zadanie 80. (1 pkt)
Równanie \(\frac{x^2-4}{(x-4)(x+4)}=0\)
A.nie ma rozwiązań.
B.ma dokładnie jedno rozwiązanie.
C.ma dokładnie dwa rozwiązania.
D.ma dokładnie cztery rozwiązania.
Zadanie 81. (1 pkt)
Wskaż \(m\), dla którego funkcja liniowa \(\ f(x)=(m−1)x+6\ \) jest rosnąca
A.\( m=-1 \)
B.\( m=0 \)
C.\( m=1 \)
D.\( m=2 \)
Zadanie 82. (1 pkt)
W ciągu arytmetycznym \((a_n)\) mamy: \(a_2=5\) i \(a_4=11\). Oblicz \(a_5\).
A.\( 8 \)
B.\( 14 \)
C.\( 17 \)
D.\( 6 \)
Zadanie 83. (1 pkt)
W ciągu geometrycznym \((a_n)\) dane są: \(a_1=2\ \) i \(\ a_2=12\). Wtedy
A.\( a_4=26 \)
B.\( a_4=432 \)
C.\( a_4=32 \)
D.\( a_4=2592 \)
Zadanie 84. (1 pkt)
Kąt \(\alpha \) jest ostry i \(\cos \alpha =\frac{3}{4}\). Wtedy \(\sin \alpha \) jest równy
A.\( \frac{1}{4} \)
B.\( \frac{\sqrt{3}}{4} \)
C.\( \frac{\sqrt{7}}{4} \)
D.\( \frac{7}{16} \)
Zadanie 85. (1 pkt)
Prosta \(l\) ma równanie \(y=-\frac{1}{4}x+7\). Wskaż równanie prostej prostopadłej do prostej \(l\).
A.\( y=\frac{1}{4}x+1 \)
B.\( y=-\frac{1}{4}x-7 \)
C.\( y=4x-1 \)
D.\( y=-4x+7 \)
Zadanie 86. (1 pkt)
Proste o równaniach \(\ y=2x+3\ \) oraz \(\ y=-\frac{1}{3}x+2\)
A.są równoległe i różne
B.są prostopadłe
C.przecinają się pod kątem innym niż prosty
D.pokrywają się
Zadanie 87. (2 pkt)
Rozwiąż nierówność \(x^2−14x+24 \gt 0\).
Zadanie 88. (2 pkt)
Rozwiąż równanie \(x^3−3x^2+2x−6=0\).
Zadanie 89. (4 pkt)
Ciąg \((9, x, 19)\) jest arytmetyczny, a ciąg \((x, 42, y, z)\) jest geometryczny. Oblicz \(x\), \(y\) oraz \(z\).
Zadanie 90. (5 pkt)
Z miejscowości \(A\) i \(B\) oddalonych od siebie o \(182\) km wyjeżdżają naprzeciw siebie dwaj rowerzyści. Rowerzysta jadący z miejscowości \(B\) do miejscowości \(A\) jedzie ze średnią prędkością mniejszą od \(25\) km/h. Rowerzysta jadący z miejscowości \(A\) do miejscowości \(B\) wyjeżdża o \(1\) godzinę wcześniej i jedzie ze średnią prędkością o \(7\) km/h większą od średniej prędkości drugiego rowerzysty. Rowerzyści spotkali się w takim miejscu, że rowerzysta jadący z miejscowości \(A\) przebył do tego miejsca \(\frac{9}{13}\) całej drogi z \(A\) do \(B\). Z jakimi średnimi prędkościami jechali obaj rowerzyści?