Obliczanie logarytmów

Drukuj

Poziom podstawowy

Szybka nawigacja do zadania numer: 5 10 15 20 25 30 .

W tym nagraniu wideo omawiam najważniejsze wiadomości dotyczące logarytmów.
Pokazuję najprostszą metodę obliczania logarytmów, omawiam wszystkie najważniejsze wzory związane z logarytmami, dziedzinę logarytmu oraz równania i nierówności logarytmiczne.

Czas nagrania: 67 min.

Poziom podstawowy

Metoda liczenia logarytmów

Przypuśćmy, że musimy obliczyć \(\log_{a}\!b\). Wynik takiego działania oznaczamy sobie przez \(x\).
Zatem mamy:
\[\log_{a}\!b=x\] Zgodnie z definicją logarytmu możemy teraz przekształcić to równanie na następujące: \[a^x=b\] Teraz z otrzymanego równania wyliczamy liczbę \(x\).

Na pierwszy rzut oka powyższa metoda może wydawać się skomplikowana, jednak w rzeczywistości jest bardzo prosta w zastosowaniu. W zamieszczonym wcześniej nagraniu wideo pokazuję jej działanie na prostych przykładach.

W celu jeszcze lepszego zapamiętania definicji logarytmu możesz spojrzeć na poniższą metodę kółka.
Pozwala ona łatwo zapamiętać, jak przeformułować problem obliczenia logarytmu, na problem znalezienia odpowiedniej potęgi. Zilustrujemy ją na prostym przykładzie:

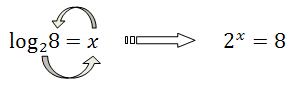Zaczynamy od dolnej dwójki, następnie idziemy do \(x\), a na koniec do dużej \(8\). Otrzymujemy w ten sposób ciąg liczb: \(2, x, 8\), które następnie zapisujemy w postaci potęgi.

Oblicz \( \log_{5}5 \).

\(1\)

Oblicz \( \log_{7}1 \).

\(0\)

Oblicz \( \log_{\frac{1}{3}}81 \).

\(-4\)

Oblicz \( \log_{2}\frac{1}{64} \).

\(-6\)

Oblicz \( \log_{\frac{1}{4}}\!\frac{1}{2} \).

\(\frac{1}{2}\)

Oblicz \( \log_{\sqrt{2}}\! 8 \).

\(6\)

Oblicz \( \log_{5}\! \sqrt[3]{5} \).

\(\frac{1}{3}\)

Oblicz \( \log_{\sqrt{5}}\! \sqrt[3]{5} \).

\(\frac{2}{3}\)

Oblicz \( \log_{\frac{1}{5}}\! \sqrt[7]{5} \).

\(-\frac{1}{7}\)

Oblicz \( \log_{2\sqrt{2}}\! 16 \).

\(\frac{8}{3}\)

Oblicz \( \log_{\sqrt[3]{3}}\! 9\sqrt{3} \).

\(\frac{15}{2}\)

Oblicz \( \log_{\frac{1}{2}}\! 16\sqrt[3]{2} \).

\(-\frac{13}{3}\)

Oblicz \( \log_{5}\! 125\sqrt{5} \).

\(\frac{7}{2}\)

Oblicz \( \log_{\frac{1}{6}}\! 36\sqrt[4]{6} \).

\(-\frac{9}{4}\)

Oblicz \( \log_{3\sqrt{3}}\! 81\sqrt[3]{3} \).

\(\frac{26}{9}\)

Oblicz \( \log_{\frac{1}{2}}\! \frac{256\sqrt{2}}{\sqrt[3]{2}} \).

\(-8\frac{1}{6}\)

Oblicz \( \log_{\frac{1}{3}}\! \frac{81\sqrt[5]{3}}{\sqrt[4]{3}} \).

\(-3\frac{19}{20}\)

Oblicz \( \log_{5}\! \frac{25\sqrt[3]{5}}{\sqrt[4]{125}} \).

\(1\frac{7}{12}\)

Oblicz \( \log_{\frac{1}{4}}\! \frac{2\sqrt[5]{64}}{\sqrt[3]{8}} \).

\(-\frac{3}{5}\)

Oblicz \( \log_{6}\! \frac{\sqrt[3]{36}}{216} \).

\(-\frac{7}{3}\)

Liczba \(2\log_{\frac{1}{5}}\! 125\) jest równa

A.\( 6 \)

B.\( -3 \)

C.\( 3 \)

D.\( -6 \)

Iloczyn \( 2\cdot \log_{\frac{1}{3}}9 \) jest równy

A.\(-6 \)

B.\(-4 \)

C.\(-1 \)

D.\(1 \)

Liczba \(2\log_3 27 - \log_2 16\) jest równa

A.\(2 \)

B.\(-8 \)

C.\(9 \)

D.\(\frac{3}{2} \)

Liczba \(\log_{3}\frac{1}{27}\) jest równa

A.\( -3 \)

B.\( -\frac{1}{3} \)

C.\( \frac{1}{3} \)

D.\( 3 \)

Liczba \(\log_2 4 + 2\log_3 1\) jest równa

A.\( 0 \)

B.\( 1 \)

C.\( 2 \)

D.\( 4 \)

Liczba \( \left ( \log_{\sqrt{3}}3\sqrt{3} \right )^4 \) jest równa

A.\(12 \)

B.\(6 \)

C.\(9 \)

D.\(81 \)

Suma \( \log_8 16+1 \) jest równa

A.\(\log_8 17 \)

B.\(\frac{3}{2} \)

C.\(\frac{7}{3} \)

D.\(3 \)

Liczba \( c=\log_{3}2 \). Wtedy

A.\(c^3=2 \)

B.\(3^c=2 \)

C.\(3^2=c \)

D.\(c^2=3 \)

Liczba \(\log_\sqrt{7}7\) jest równa

A.\( 2 \)

B.\( 7 \)

C.\( \sqrt{7} \)

D.\( \frac{1}{2} \)