Monotoniczność ciągu
Poziom podstawowy
Ciąg liczbowy nazywamy monotonicznym jeżeli jest rosnący, albo malejący, albo stały, albo nierosnący, albo niemalejący. Najważniejsze z tych przypadków są ciągi: rosnące oraz malejące.
Definicja
Ciąg \((a_n)\) nazywamy ciągiem rosnącym jeżeli dla każdej liczby \(n\in \mathbb{N}_+\) prawdziwa jest nierówność \(a_{n+1} \gt a_n\).Żeby udowodnić, że ciąg jest rosnący, to należy pokazać, że dla dowolnego \(n\in \mathbb{N}_+\) zachodzi: \[a_{n+1} - a_n \gt 0\] Do wykonania takiego zadania należy umieć zapisać wzór na wyraz \(a_{n+1}\) ciągu. W tym celu wystarczy podstawić we wzorze \(a_n\) w miejsce \(n\) wyrażenie \(n+1\).
Dany jest ciąg o wzorze ogólnym \(a_n=5n^2-n+3\). Wyznacz wzór na \(a_{n+1}\).
\[a_{n+1}=5(n+1)^2-(n+1)+3=5n^2+10n+5-n-1+3=5n^2+9n+7\]
\[\begin{split}a_{n+1}&=5(n+1)^2-(n+1)+3=\\[6pt] &=5n^2+10n+5-n-1+3=\\[6pt] &=5n^2+9n+7\end{split}\]
Zatem: \[a_{n+1}=5n^2+9n+7\] Ciąg dany wzorem \(a_n=2n-3\) jest ciągiem rosnącym. Wypiszmy kilka początkowych wyrazów tego ciągu: \[-1,1,3,5,7,...\] i zaznaczmy je na wykresie: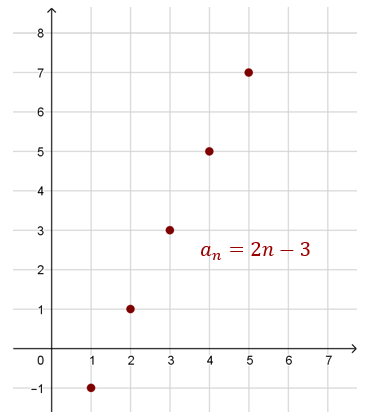 
Wykażemy, że ten ciąg jest rosnący badając znak różnicy \(a_{n+1} - a_n\). Mamy: \[a_n=2n-3 \quad \text{oraz} \quad a_{n+1}=2(n+1)-3\] Zatem: \[a_{n+1} - a_n=2n+2-3-(2n-3)=2n-1-2n+3=2\] Czyli: \[a_{n+1} - a_n=2\gt 0\] Różnica wyszła dodatnia dla dowolnego \(n\in \mathbb{N}_+\), zatem ciąg jest rosnący.
Wykażemy, że ten ciąg jest rosnący badając znak różnicy \(a_{n+1} - a_n\). Mamy: \[a_n=2n-3 \quad \text{oraz} \quad a_{n+1}=2(n+1)-3\] Zatem: \[a_{n+1} - a_n=2n+2-3-(2n-3)=2n-1-2n+3=2\] Czyli: \[a_{n+1} - a_n=2\gt 0\] Różnica wyszła dodatnia dla dowolnego \(n\in \mathbb{N}_+\), zatem ciąg jest rosnący. Definicja
Ciąg \((a_n)\) nazywamy ciągiem malejącym jeżeli dla każdej liczby \(n\in \mathbb{N}_+\) prawdziwa jest nierówność \(a_{n+1} \lt a_n\).Żeby udowodnić, że ciąg jest malejący, to należy pokazać, że dla dowolnego \(n\in \mathbb{N}_+\) zachodzi: \[a_{n+1} - a_n \lt 0\]
Ciąg dany wzorem \(a_n=2-n\) jest ciągiem malejącym. Wypiszmy kilka początkowych wyrazów tego ciągu: \[1,0,-1,-2,-3,-4,...\] i zaznaczmy je na wykresie: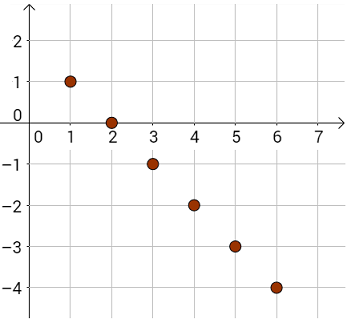 
Wykażemy, że ten ciąg jest malejący badając znak różnicy \(a_{n+1} - a_n\). Mamy: \[a_n=2-n \quad \text{oraz} \quad a_{n+1}=2-(n+1)\] Zatem: \[a_{n+1} - a_n=2-n-1-(2-n)=1-n-2+n=-1\] Czyli: \[a_{n+1} - a_n=-1\lt 0\] Różnica wyszła ujemna dla dowolnego \(n\in \mathbb{N}_+\), zatem ciąg jest malejący.
Wykażemy, że ten ciąg jest malejący badając znak różnicy \(a_{n+1} - a_n\). Mamy: \[a_n=2-n \quad \text{oraz} \quad a_{n+1}=2-(n+1)\] Zatem: \[a_{n+1} - a_n=2-n-1-(2-n)=1-n-2+n=-1\] Czyli: \[a_{n+1} - a_n=-1\lt 0\] Różnica wyszła ujemna dla dowolnego \(n\in \mathbb{N}_+\), zatem ciąg jest malejący. Definicja
Ciąg liczbowy stały, to taki w którym wszystkie wyrazy są równe. Ciąg stały \(a_n=4\) ma wszystkie wyrazy równe: \[4,4,4,4,4,...\] Oto interpretacja graficzna tego ciągu: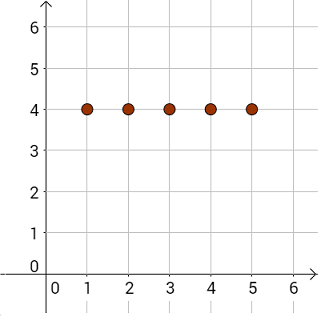 
Przykład ciągu który nie jest monotoniczny: \[1, -2,3-4,5,...\]
Definicja
Ciąg \((a_n)\) nazywamy ciągiem nierosnącym jeżeli dla każdej liczby \(n\in \mathbb{N}_+\) prawdziwa jest nierówność \(a_{n+1} \le a_n\). Ciąg liczbowy nierosnący, to taki ciąg w którym kolejne liczby są coraz mniejsze lub równe, np.: \[5,4,4,3,2,...\] Oto interpretacja graficzna tego ciągu: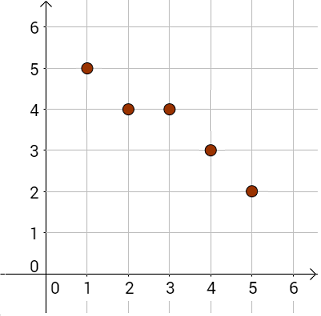 
Definicja
Ciąg \((a_n)\) nazywamy ciągiem niemalejącym jeżeli dla każdej liczby \(n\in \mathbb{N}_+\) prawdziwa jest nierówność \(a_{n+1} \ge a_n\). Ciąg liczbowy niemalejący, to taki ciąg w którym kolejne liczby są coraz większe lub równe, np.: \[2,3,3,4,5,...\] Oto interpretacja graficzna tego ciągu: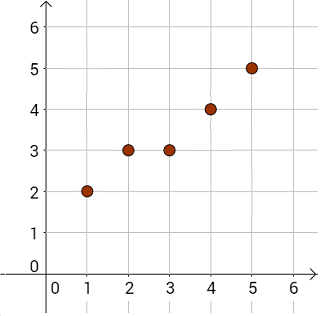 
Zbadaj czy nieskończony ciąg \((a_n)\) o wzorze ogólnym \(a_n=\frac{n}{3n+1}\) jest monotoniczny.
Zbadaj czy nieskończony ciąg \((a_n)\) o wzorze ogólnym \(a_n=n^2-8n\) jest rosnący, czy malejący.
Tematy nadrzędne i sąsiednie