Mediana

Drukuj

Poziom podstawowy

Definicja

Mediana - to wartość środkowa, wśród danych uporządkowanych od najmniejszej do największej.

Jeżeli mamy nieparzystą liczbę danych, to istnieje dokładnie jedna wartość środkowa.
Jeżeli mamy parzystą liczbę danych, to mediana jest równa średniej arytmetycznej dwóch środkowych wartości.

Oblicz medianę liczb: \(6, 4, 2, 4, 4\).

Najpierw wypisujemy liczby w kolejności niemalejącej: \[2, 4, \color{Red}4\color{Black}, 4, 6\] Mediana to liczba środkowa. Zatem mediana jest równa \(4\).

Oblicz medianę liczb: \(5, 8, -1, 6, 6, 1, 10\).

Najpierw wypisujemy liczby w kolejności niemalejącej: \[-1, 1, 5, \color{Red}6\color{Black}, 6, 8, 10\] Mediana to liczba środkowa. Zatem mediana jest równa \(6\).

Oblicz medianę liczb: \(7,8,3,4,9,2\).

Najpierw wypisujemy liczby w kolejności niemalejącej: \[2,3, \color{Red}4,7\color{Black}, 8,9\] W tym przypadku nie mamy jednej liczby środkowej, zatem bierzemy dwie liczby środkowe: \(4\) oraz \(7\), a następnie liczymy ich średnią arytmetyczną: \[\frac{4+7}{2}=\frac{11}{2}\] Zatem mediana jest równa \(\frac{11}{2}\).

W kolejnych sześciu rzutach kostką otrzymano następujące wyniki: \(6, 3, 1, 2, 5, 5\). Mediana tych wyników jest równa:

A.\( 3 \)

B.\( 3{,}5 \)

C.\( 4 \)

D.\( 5 \)

Oblicz medianę oraz średnią arytmetyczną danych: \(1, 2, 4, 7, 1\).

mediana: \(2\), średnia arytmetyczna: \(3\)

Mediana danych: \(0, 1, 1, 2, 3, 1\) jest równa

A.\( 1 \)

B.\( 1{,}5 \)

C.\( 2 \)

D.\( 2{,}5 \)

Mediana danych: \(-4, 2, 6, 0, 1\) jest równa

A.\( 6 \)

B.\( 0 \)

C.\( 2{,}5 \)

D.\( 1 \)

Oblicz medianę danych: \(0, 1, 3, 3, 1, 1, 2, 1\).

\(1\)

Wyniki sprawdzianu z matematyki przedstawione są w tabeli:

Ocena	1	2	3	4	5	6
Liczba uczniów	2	3	7	6	4	2

Mediana ocen ze sprawdzianu jest równa

A.\( 3{,}5 \)

B.\( 3 \)

C.\( 4 \)

D.\( 4{,}5 \)

Mediana danych przedstawionych w tabeli liczebności jest równa

wartość	\(0\)	\(1\)	\(2\)	\(3\)
liczebność	\(5\)	\(2\)	\(1\)	\(1\)

A.\( 0 \)

B.\( 0{,}5 \)

C.\( 1 \)

D.\( 5 \)

Oblicz medianę danych przedstawionych w postaci tabeli liczebności

wartość	\(0\)	\(1\)	\(2\)	\(3\)
liczebność	\(4\)	\(3\)	\(1\)	\(1\)

\(1\)

Na diagramie poniżej przedstawiono ceny pomidorów w szesnastu wybranych sklepach.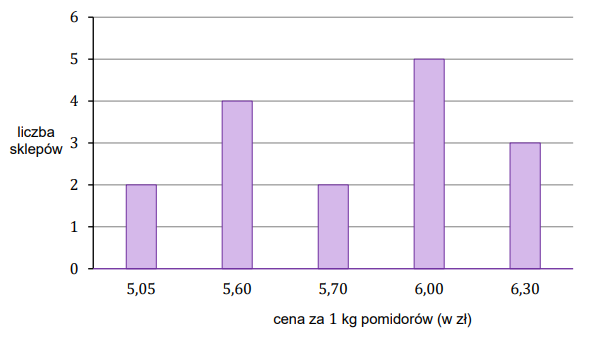

Uzupełnij tabelę. Wpisz w każdą pustą komórkę tabeli właściwą odpowiedź, wybraną spośród oznaczonych literami A–E.

1.	Mediana ceny kilograma pomidorów w tych wybranych sklepach jest równa
2.	Średnia cena kilograma pomidorów w tych wybranych sklepach jest równa

A.\( 5{,}80 \)

B.\( 5{,}73 \)

C.\( 5{,}85 \)

D.\( 6{,}00 \)

E.\( 5{,}70 \)

C A

Wyniki sprawdzianu z matematyki są przedstawione na diagramie.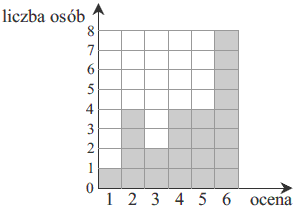

Mediana ocen uzyskanych przez uczniów jest równa

A.\( 6 \)

B.\( 5 \)

C.\( 4{,}5 \)

D.\( 4 \)

W drużynie koszykarskiej zawodnicy mają wzrost odpowiednio: \(191\) cm, \(210\) cm, \(205\) cm, \(204\) cm, \(212\) cm. Mediana zbioru tych wartości wynosi

A.\( 204 \) cm

B.\( 205 \) cm

C.\( 207 \) cm

D.\( 210 \) cm

W drużynie siatkarskiej zawodnicy mają wzrost odpowiednio: \(207\) cm, \(205\) cm, \(205\) cm, \(197\) cm, \(212\) cm, \(216\) cm. Mediana zbioru tych wartości wynosi

A.\( 197 \) cm

B.\( 201 \) cm

C.\( 205 \) cm

D.\( 206 \) cm

Pewna firma zatrudnia \(6\) osób. Dyrektor zarabia \(8000\) zł, a pensje pozostałych pracowników są równe: \(2000\) zł, \(2800\) zł, \(3400\) zł, \(3600\) zł, \(4200\) zł. Mediana zarobków tych \(6\) osób jest równa

A.\( 3400 \) zł

B.\( 3500 \) zł

C.\( 6000 \) zł

D.\( 7000 \) zł

Ciąg \((9, 18, x)\) jest geometryczny, a ciąg \((x, 30, y)\) jest arytmetyczny.
Oblicz medianę liczb: \(10, x, y, 12, 12, 18, 30.\)

\(18\)

Mediana uporządkowanego niemalejąco zestawu sześciu liczb: \(1, 2, 3, x, 5, 8\) jest równa \(4\). Wtedy

A.\( x=2 \)

B.\( x=3 \)

C.\( x=4 \)

D.\( x=5 \)

Mediana zestawu danych \( 2, 12, a, 10, 5, 3 \) jest równa \( 7 \). Wówczas

A.\(a=4 \)

B.\(a=6 \)

C.\(a=7 \)

D.\(a=9 \)

Średnia arytmetyczna liczb: \( x,13,7,5,5,3,2,11 \) jest równa \( 7 \). Mediana tego zestawu liczb jest równa

A.\(6 \)

B.\(7 \)

C.\(10 \)

D.\(5 \)

Średnia arytmetyczna zestawu danych: \( 3, 8, 3, 11, 3, 10, 3, x \) jest równa \( 6 \). Mediana tego zestawu jest równa

A.\( 5 \)

B.\( 6 \)

C.\( 7 \)

D.\( 8 \)

Medianą zestawu danych \(9, 1, 4, x, 7, 9\) jest liczba \(8\). Wtedy \(x\) może być równe

A.\( 8 \)

B.\( 4 \)

C.\( 7 \)

D.\( 9 \)

Abiturient jednego z liceów zestawił w tabeli oceny ze swojego świadectwa ukończenia szkoły.

Ocena	6	5	4	3	2
Liczba ocen	2	3	5	5	1

Mediana przedstawionego zestawu danych jest równa

A.\( 3 \)

B.\( 3{,}5 \)

C.\( 4 \)

D.\( 4{,}5 \)

Cztery liczby: \(2, 3, a, 8\), tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: \(5, 3, 6, 8, 2\). Zatem

A.\( a=7 \)

B.\( a=6 \)

C.\( a=5 \)

D.\( a=4 \)

Liczba \(x\) jest dodatnia. Mediana zestawu czterech liczb: \(1+x,\ 1+2x,\ 4+3x,\ 1\), jest równa \(10\). Wtedy

A.\( x=6 \)

B.\( x=5{},5 \)

C.\( x=2{,}5 \)

D.\( x=1 \)

Sześciowyrazowy ciąg liczbowy \((1,\ 2,\ 2x,\ x+2,\ 5,\ 6)\) jest niemalejący. Mediana wyrazów tego ciągu jest równa \(4\). Wynika stąd, że

A.\( x=1 \)

B.\( x=\frac{3}{2} \)

C.\( x=2 \)

D.\( x=\frac{8}{3} \)