Matura rozszerzona - kurs - część 40 - zadania

Drukuj

Poziom rozszerzony

Cały kurs na: http://www.matemaks.pl/matematyka-matura-rozszerzona-kurs.html.

Wyznacz równanie okręgu przechodzącego przez punkt \(A = (2, 1)\) i stycznego do obu osi układu współrzędnych. Rozważ wszystkie przypadki.

\((x-1)^2+(y-1)^2=1\) lub \((x-5)^2+(y-5)^2=25\)

Środkiem okręgu o równaniu \( (x+2)^2+(y-3)^2=16 \) jest punkt:

A.\(S=(2,3) \)

B.\(S=(-2,3) \)

C.\(S=(2,-3) \)

D.\(S=(-2,-3) \)

Liczba punktów wspólnych okręgu o równaniu \( (x+2)^2+(y-3)^2=4\ \) z osiami układu współrzędnych jest równa

A.\(0 \)

B.\(1 \)

C.\(2 \)

D.\(4 \)

Punkt \( P=(-1,0) \) leży na okręgu o promieniu \( 3 \). Równanie tego okręgu może mieć postać

A.\((x+1)^2+y^2=9 \)

B.\(x^2+\left ( y-\sqrt{2} \right )^2=3 \)

C.\((x+1)^2+(y+3)^2=9 \)

D.\((x+1)^2+y^2=3 \)

Okrąg przedstawiony na rysunku ma środek w punkcie \(O=(3,1)\) i przechodzi przez punkty \(S=(0,4)\) i \(T=(0,-2)\). Okrąg ten jest opisany przez równanie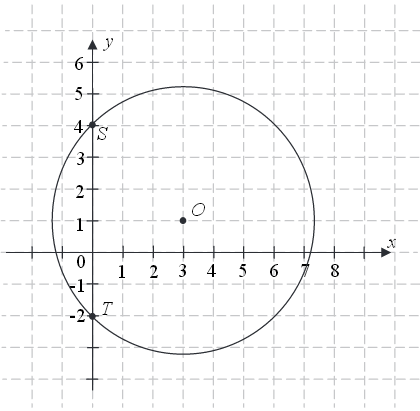

A.\( (x+3)^2+(y+1)^2=18 \)

B.\( (x-3)^2+(y+1)^2=18 \)

C.\( (x-3)^2+(y-1)^2=18 \)

D.\( (x+3)^2+(y-1)^2=18 \)

Okrąg opisany równaniem \((x−3)^2 + (y + 2)^2 = r^2\) jest styczny do osi \(Oy\). Promień \(r\) tego okręgu jest równy

A.\( \sqrt{13} \)

B.\( \sqrt{5} \)

C.\( 3 \)

D.\( 2 \)