Matura rozszerzona - kurs - część 32 - zadania
Poziom rozszerzony
Cały kurs na: http://www.matemaks.pl/matematyka-matura-rozszerzona-kurs.html.Dany jest trójkąt \(ABC\) o polu równym \(P\). Odcinki \(IJ\) i \(GH\), których końce leżą na bokach trójkąta, są równoległe do boku \(AB\) i przecinają wysokość \(CD\) w punktach \(E\) i \(F\) takich, że \(|CE|=|DF|=\frac{1}{4}\cdot |CD|\) (zobacz rysunek). 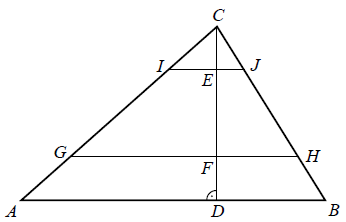 Pole trapezu \(GHJI\) jest równe
Pole trapezu \(GHJI\) jest równe
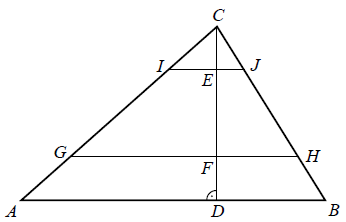 Pole trapezu \(GHJI\) jest równe
Pole trapezu \(GHJI\) jest równe A.\( \frac{1}{2}P \)
B.\( \frac{9}{16}P \)
C.\( \frac{2}{3}P \)
D.\( \frac{3}{4}P \)
Z wierzchołków kwadratu poprowadzono do odpowiednich boków proste pod takim samym kątem \(\alpha \), mniejszym od \(45^\circ \), (zobacz rysunek). Proste te wyznaczają w szczególności trójkąt (zacieniowany) o polu \(9\) i czworokąt (zacieniowany) o polu \(7\). Wyznacz pole kwadratu. 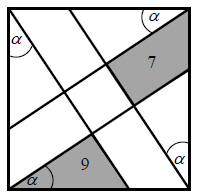
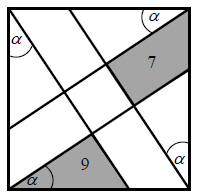
Na podstawie \(AB\) trapezu \(ABCD\) (\(|AB|\gt |CD|\)) wyznaczono taki punkt \(E\), że czworokąt \(AECD\) jest równoległobokiem. Przekątna \(BD\) przecina odcinki \(CA\) i \(CE\) odpowiednio w punktach \(F\) i \(G\). Odcinki \(DG\) i \(BF\) są równej długości. Uzasadnij, że \(\frac{|AB|}{|CD|}=\frac{1+\sqrt{5}}{2}\). 

Dany jest prostokąt \(ABCD\). Okrąg wpisany w trójkąt \(BCD\) jest styczny do przekątnej \(BD\) w punkcie \(N\). Okrąg wpisany w trójkąt \(ABD\) jest styczny do boku \(AD\) w punkcie \(M\), a środek \(S\) tego okręgu leży na odcinku \(MN\), jak na rysunku. 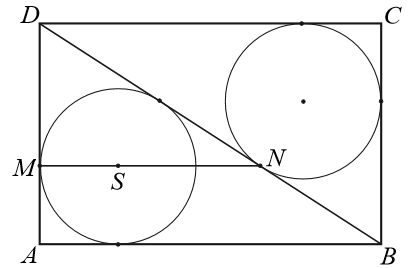 Wykaż, że \(|MN|=|AD|\).
Wykaż, że \(|MN|=|AD|\).
 Wykaż, że \(|MN|=|AD|\).
Wykaż, że \(|MN|=|AD|\).Tematy nadrzędne