Matura podstawowa 2026 - luty - próbna z Matemaksem
Poziom podstawowy
Materiały do pobrania:
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\frac{(5\sqrt{2}+\sqrt{18})^2}{4^{4}\cdot 8^8}\) jest równa A.\(2^{-30}\)
B.\(2^{-25}\)
C.\(2^{-15}\)
D.\(2^{-10}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\log_{5}105-3\log_{5}\sqrt[3]{21}\) jest równa A.\(-1\)
B.\(0\)
C.\(1\)
D.\(\log_{5}\frac{105}{\sqrt[3]{21}}\)
Dane są liczby \(a=|1+\sqrt{2}|\) oraz \(b=|1-\sqrt{2}|\).
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Liczba \(a+b\) jest liczbą całkowitą. | P | F |
| Liczba \(a\cdot b\) jest liczbą całkowitą. | P | F |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zbiorem wszystkich rozwiązań nierówności \[ \frac{2-x}{4}>\;x-\frac{1}{2} \] jest przedział A.\(\left(-\infty,\,\frac{4}{5}\right)\)
B.\(\left(-\infty,\,\frac{2}{3}\right)\)
C.\(\left(\frac{2}{3},\,+\infty\right)\)
D.\(\left(\frac{4}{5},\,+\infty\right)\)
Wykaż, że dla każdej liczby całkowitej \(a\), która przy dzieleniu przez \(7\) daje resztę \(2\), oraz dla każdej liczby całkowitej \(b\), która przy dzieleniu przez \(7\) daje resztę \(5\), liczba \(a^{2}+2b^{2}+2\) jest podzielna przez \(7\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Średnia arytmetyczna wszystkich rozwiązań równania \((2x+2)(3x-6)(5x+15)=0\) jest równa A.\(\left(-\frac{2}{3}\right)\)
B.\(\left(-\frac{1}{3}\right)\)
C.\(0\)
D.\(\frac{1}{3}\)
Serwis streamingowy wypłacił dwóm artystom łącznie \(180\ 000\) złotych za odtworzenia ich utworów 2024 roku. W roku 2025 wynagrodzenie jednego artysty wzrosło o \(20\%\), drugiego spadło o \(30\%\), ale ich łączne wynagrodzenie wyniosło tyle samo co w roku poprzednim.
Oblicz, jakie wynagrodzenia otrzymali obaj artyści w 2025 roku. Zapisz obliczenia.
Rozwiąż nierówność \[ x(x+11)\le x-25 \] Zapisz obliczenia.
Rozwiąż równanie \[\frac{x}{2x-1}=1-\frac{3-x}{3+x}\] Zapisz konieczne założenie i obliczenia.
Funkcja \(f\) jest określona następująco: \[ f(x)= \begin{cases} 4 & \text{dla } x\in[-5,-2)\\ -2x & \text{dla } x\in[-2,1]\\ x-\frac{5}{2} & \text{dla } x\in(1,4) \end{cases} \] Wykres funkcji \(y=f(x)\) przedstawiono w kartezjańskim układzie współrzędnych \((x, y)\) na rysunku poniżej. 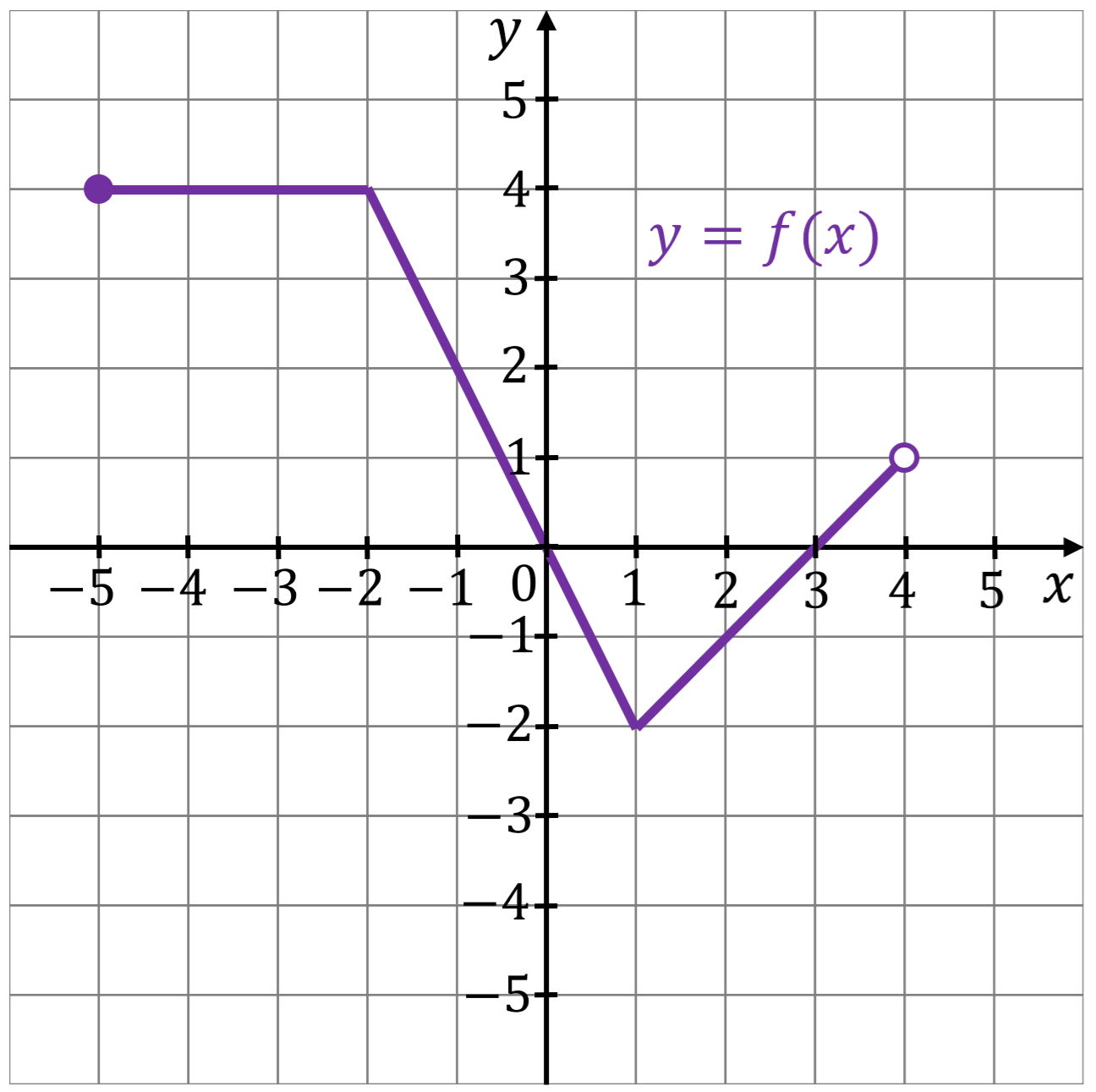

Uzupełnij zdania. Wpisz odpowiednie przedziały w wykropkowanych miejscach, aby zdania były prawdziwe.
- Dziedziną funkcji \(f\) jest przedział …………………… .
- Zbiorem wszystkich argumentów, dla których funkcja \(f\) jest stała, jest przedział …………………… .
- Suma miejsc zerowych funkcji \(f\) jest równa …………………… .
- Liczba rozwiązań równania \(f(x)=-1,(3)\) jest równa …………………… .
Funkcja liniowa \(f\) jest określona wzorem \(f(x)=(10-2k)x+\frac{k}{5}\), gdzie \(k\) jest liczbą rzeczywistą. Funkcja \(f\) jest malejąca.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(k\) należy do przedziału A.\((-\infty,-5)\)
B.\((-5,5)\)
C.\(\left(-\frac{1}{5}, \frac{1}{5}\right)\)
D.\((5,+\infty)\)
W kartezjańskim układzie współrzędnych \((x, y)\) wykresem funkcji kwadratowej \(f\) jest parabola, której osią symetrii jest prosta \(x=2\). Ta parabola przechodzi przez punkt o współrzędnych \((5, 0)\). Największa wartość jaką osiąga funkcja \(f\) na przedziale \(\langle 0, 2\rangle \) jest równa \(1\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wierzchołek paraboli będącej wykresem funkcji kwadratowej \(f\) ma współrzędne: A.\( (2, 0) \)
B.\( (2, 1) \)
C.\( (1, 2) \)
D.\( (0, 1) \)
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Suma miejesc zerowych funkcji \(f\) jest równa \(6\). | P | F |
| Istnieje taki argument ujemny dla którego funkcja \(f\) przyjmuje wartość dodatnią. | P | F |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wzór funkcji kwadratowej \(f\) w postaci kanonicznej, to: A.\( f(x)=-\frac{1}{9}(x-2)^2+1 \)
B.\( f(x)=\frac{1}{9}(x-2)^2+1 \)
C.\( f(x)=-\frac{1}{9}(x+2)^2+1 \)
D.\( f(x)=\frac{1}{9}(x+2)^2-1 \)
Funkcja wykładnicza \(f\) jest określona wzorem \(f(x)=\left(\frac{1}{3}\right)^x+2\) dla każdej dodatniej liczby rzeczywistej \(x\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Funkcja \(f\) przyjmuje dla argumentu \((-2)\) wartość: A.\( \frac{7}{3} \)
B.\( \frac{19}{9} \)
C.\( 5 \)
D.\( 11 \)
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Funkcja \(g(x)=f(x-3)\) ma miejsce zerowe. | P | F |
| Funkcja \(g(x)=f(x)-3\) ma miejsce zerowe. | P | F |
Ciąg \(\left(a_{n}\right)\) jest określony następująco: \[ \left\{\begin{array}{l} a_{1}=-1 \\ a_{n+1}=n^2+a_{n} \end{array} \right. \] dla każdej liczby naturalnej \(n \geq 1\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Suma trzech pierwszych wyrazów tego ciągu jest równa A.\(0\)
B.\(1\)
C.\(2\)
D.\(3\)
Dany jest ciąg arytmetyczny \(\left(a_{n}\right)\) określony dla każdej liczby naturalnej \(n \geq 1\), w którym \(a_{4}=\sqrt{2}\) oraz \(a_{8}=5\sqrt{2}\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Szósty wyraz ciągu \(\left(a_{n}\right)\) jest równy A.\(2\)
B.\(2\sqrt{2}\)
C.\(3\sqrt{2}\)
D.\(\frac{\sqrt{2}}{2}\)
Wyznacz wszystkie wartości parametru \(m\), dla którego trzywyrazowy ciąg \[ \left(2m-1,\ m,\ 2m+1\right) \] jest geometryczny. Zapisz obliczenia.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Kąt \(\alpha\) jest ostry i spełnia warunek \[\,\mathrm{tg}\,\alpha - \cos^{2} \alpha = \frac{1}{3\cos \alpha }+\sin^2\alpha-1\] Sinus kąta \(\alpha\) jest równy A.\(\dfrac{1}{3}\)
B.\(\dfrac{\sqrt{3}}{2}\)
C.\(\dfrac{1}{4}\)
D.\(\dfrac{\sqrt{3}}{5}\)
Dany jest trójkąt prostokątny \(ABC\) o kątach ostrych \(\alpha\) i \(\beta\) oraz boku \(BC\) długości \(2\sqrt{5}\) (zobacz rysunek). Cosinus kąta \(\beta\) jest równy \(\frac{2}{3}\). 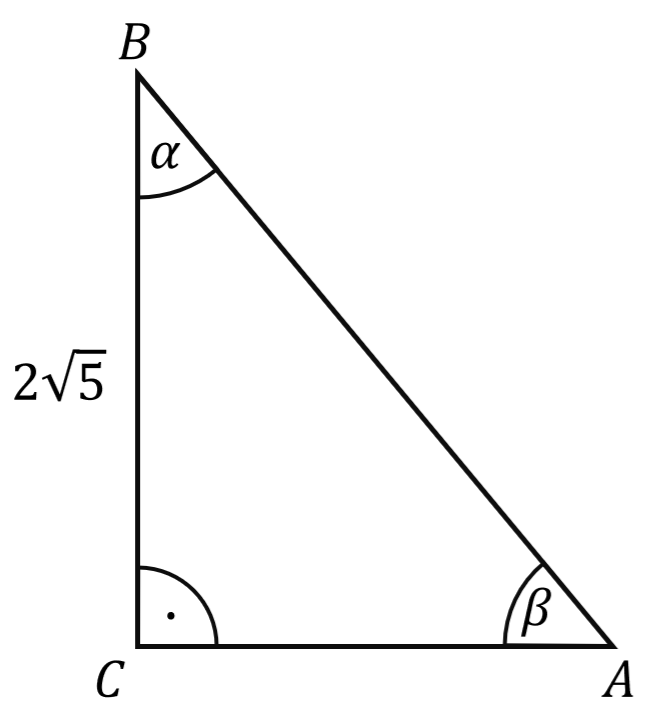

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Tangens kąta \(\alpha \) jest równy A.\( \frac{\sqrt{5}}{5} \)
B.\( \frac{2\sqrt{5}}{6} \)
C.\( \frac{2\sqrt{5}}{5} \)
D.\( \frac{\sqrt{5}}{3} \)
Oblicz obwód okręgu opisanego na trójkącie \(ABC\). Zapisz obliczenia.
Pole koła wpisanego w trójkąt równoboczny \(ABC\) jest równe \(36\pi\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole trójkąta \(ABC\) jest równe A.\( 27\sqrt{3} \)
B.\( 54\sqrt{3} \)
C.\( 108\sqrt{3} \)
D.\( 216\sqrt{3} \)
Na czworokącie \(ABCD\) opisano okrąg. Przekątne czworokąta \(ABCD\) przecinają się w punkcie \(S\). Kąt \(ABD\) ma miarę \(50^\circ\), a kąt \(BDC\) ma miarę \(60^\circ\) (zobacz rysunek). 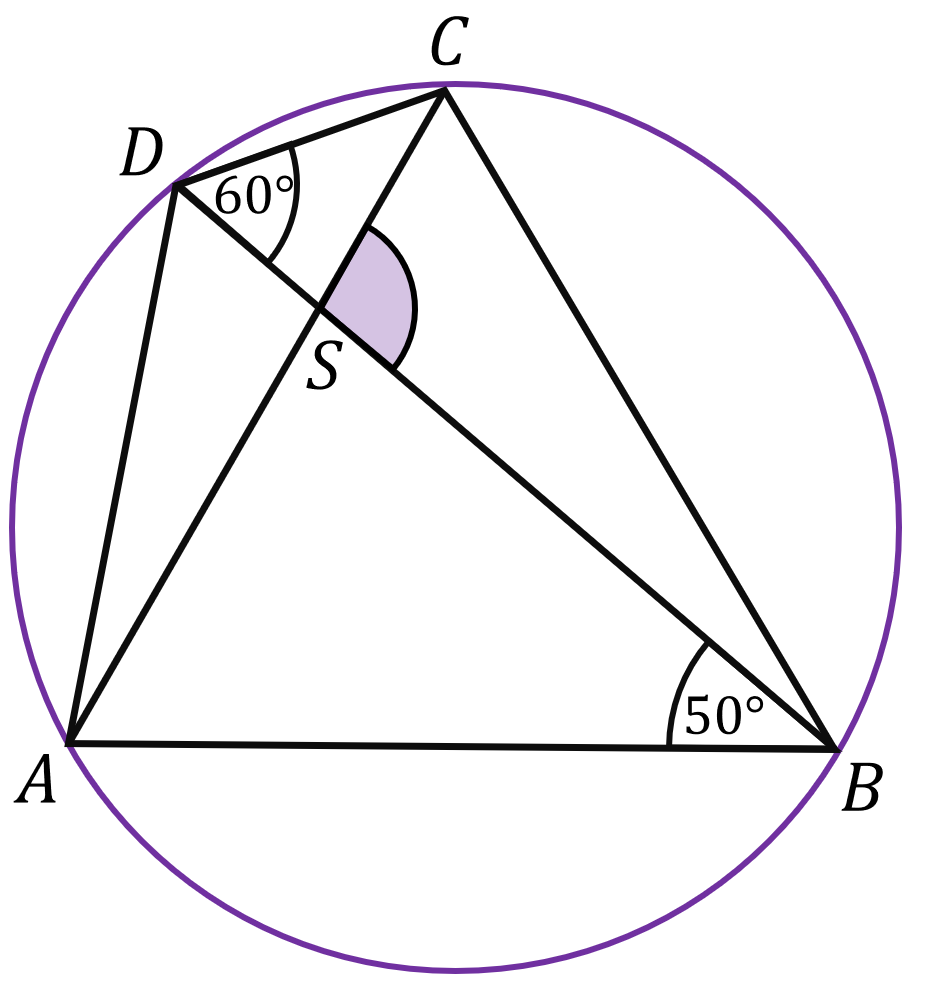

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miara kąta \(BSC\) jest równa A.\( 100^\circ \)
B.\( 110^\circ \)
C.\( 120^\circ \)
D.\( 130^\circ \)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Jeżeli promień okręgu opisanego na czworokącie \(ABCD\) ma długość \(r\), to wówczas długość łuku \(BC\) jest równa A.\( \frac{55}{360}\cdot 2\pi r \)
B.\( \frac{60}{360}\cdot 2\pi r \)
C.\( \frac{110}{360}\cdot 2\pi r \)
D.\( \frac{120}{360}\cdot 2\pi r \)
W trójkącie prostokątnym \(ABC\) poprowadzono wysokość \(CD\) z wierzchołka kąta prostego, która podzieliła przeciwprostokątną \(BC\) na odcinki długości \(9\) i \(3\) (zobacz rysunek). 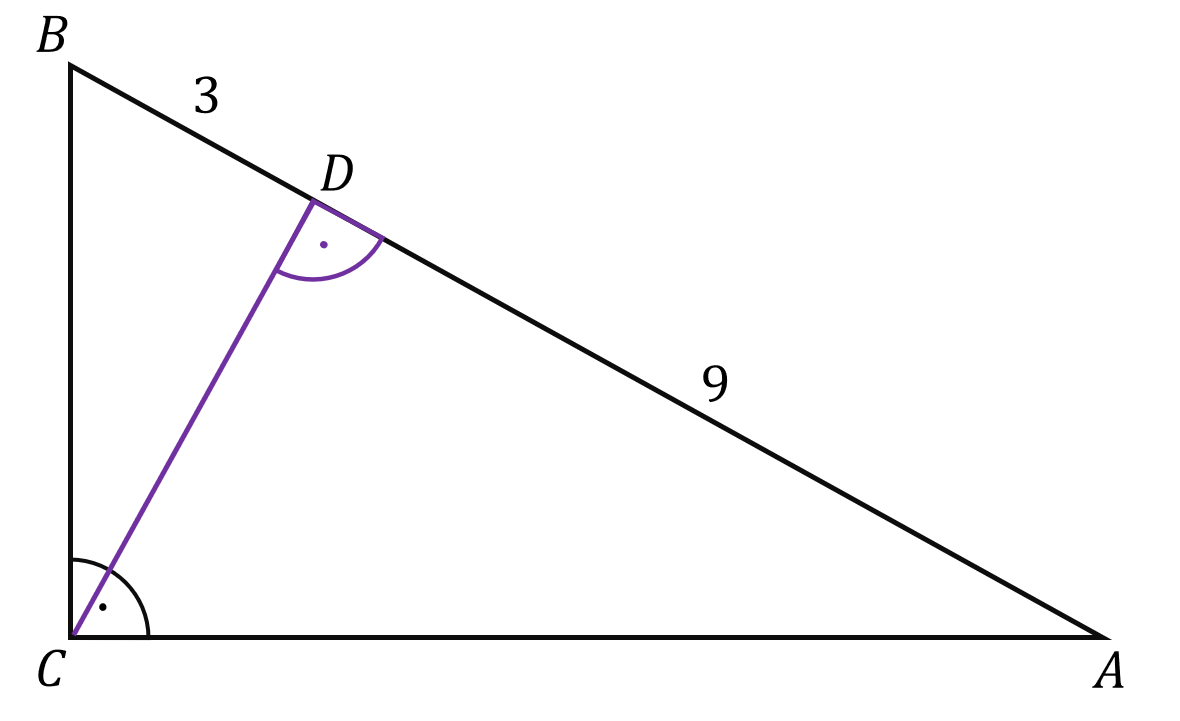

Oblicz pole i obwód trójkąta \(ABC\). Zapisz obliczenia.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
W kartezjańskim układzie współrzędnych \((x, y)\) proste \(k\) oraz \(l\) są określone równaniami \[ \begin{aligned} k:&\; y=(2m+1)\,x+m\\ l:&\; y=(m^2+1)x-m \end{aligned} \] Proste \(k\) oraz \(l\) nie mają punktów wspólnych, gdy liczba \(m\) jest równa A.\((-2)\)
B.\(0\)
C.\(1\)
D.\(2\)
W kartezjańskim układzie współrzędnych \((x, y)\) dane są cztery okręgi: \(o_{1}, o_{2}, o_{3}, o_{4}\), o równaniach: \[ \begin{aligned} & o_{1}:(x-1)^{2}+(y-2)^{2}=2 \\[6pt] & o_{2}:(x+3)^{2}+(y+1)^{2}=8 \\[6pt] & o_{3}:(x-3)^{2}+(y-2)^{2}=9 \\[6pt] & o_{4}:(x-2)^{2}+(y+3)^{2}=10 \end{aligned} \]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Okręgiem, który ma dokładnie \(3\) punkty wspólne z osiami układu współrzędnych \((x, y)\), jest A.\(o_{1}\)
B.\(o_{2}\)
C.\(o_{3}\)
D.\(o_{4}\)
W kartezjańskim układzie współrzędnych \((x, y)\) dane są dwa punkty \(A=(1, 0)\) oraz \(B=(-2, 1)\), które są wierzchołkami rombu \(ABCD\). Osią symetrii rombu \(ABCD\) jest oś \(OX\) układu współrzędnych.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole tego rombu jest równe A.\( 6 \)
B.\( 9 \)
C.\( 12 \)
D.\( 18 \)
Pole podstawy ostrosłupa prawidłowego trójkątnego jest równe \(\frac{15\sqrt{3}}{4}\). Krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem \(\alpha \), takim, że \(\cos \alpha =\frac{1}{3}\).
Oblicz objętość tego ostrosłupa. Zapisz obliczenia.
Tworząca stożka ma długość \(10\). Kąt rozwarcia stożka ma miarę \(90^{\circ}\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Objętość tego stożka jest równa A.\(250\sqrt{2}\pi\)
B.\(\frac{250\sqrt{2}}{3}\pi\)
C.\(\frac{500\sqrt{2}}{3}\pi\)
D.\(500\sqrt{2}\pi\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wszystkich liczb naturalnych czterocyfrowych podzielnych przez \(5\), w zapisie których cyfry nie powtarzają się jest A.\( 2\cdot 9\cdot 8\cdot 7\)
B.\( 2\cdot 8\cdot 8\cdot 7\)
C.\( 9\cdot 8\cdot 7 + 8\cdot 7\cdot 6 \)
D.\( 9\cdot 8\cdot 7 + 8\cdot 8\cdot 7\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Doświadczenie losowe polega na trzykrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od 1 do 6. Zdarzenie \(A\) polega na tym, że iloczyn liczb wyrzuconych oczek jest równy \(8\). Prawdopodobieństwo zdarzenia \(A\) jest równe A.\(\dfrac{1}{216}\)
B.\(\dfrac{6}{216}\)
C.\(\dfrac{7}{216}\)
D.\(\dfrac{8}{216}\)
Program komputerowy wykonał \(99\) losowań liczb, za każdym razem losując jedną liczbę ze zbioru \(\{0, 1, 2, 3\}\). Wyniki losowań zebrano w tabeli: 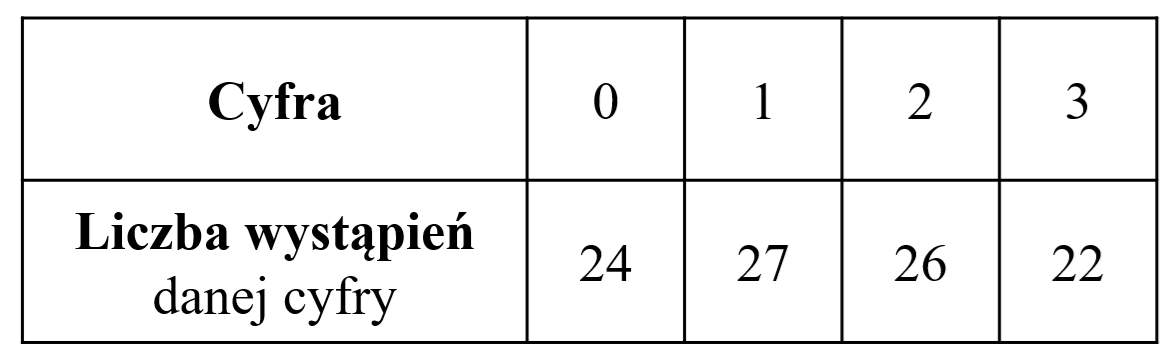 Mediana zbioru wylosowanych liczb jest równa
Mediana zbioru wylosowanych liczb jest równa
 Mediana zbioru wylosowanych liczb jest równa
Mediana zbioru wylosowanych liczb jest równa A.\( 1 \)
B.\( 1,5 \)
C.\( 2 \)
D.\( 2,5 \)
W wyniku przeprowadzonej analizy pewnego przedsiębiorstwa ustalono, że zysk z produkcji jest zależny od liczby zatrudnionych pracowników i wyraża się następującym wzorem: \[ Z(x)=\frac{17}{29}x(130-x) \] gdzie:
\(x\) - liczba zatrudnionych pracowników
\(Z\) - miesięczny zysk z produkcji przedsiębiorstwa
\(x\) - liczba zatrudnionych pracowników
\(Z\) - miesięczny zysk z produkcji przedsiębiorstwa
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miesięczny zysk z produkcji przedsiębiorstwa będzie największy, jeżeli liczba zatrudnionych pracowników wyniesie A.\(58\)
B.\(65\)
C.\(70\)
D.\(87\)
Tematy nadrzędne i sąsiednie