Matura 2025 czerwiec PR

Drukuj

Poziom rozszerzony

Sklep AGD prowadzi sprzedaż wysyłkową pralek. Prawdopodobieństwo uszkodzenia podczas transportu pralki wysłanej przez ten sklep do klienta jest równe \(0{,}02\).

Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że spośród 10 pralek wysłanych dziesięciu klientom przez ten sklep co najwyżej jedna ulegnie uszkodzeniu podczas transportu. Wynik zapisz w postaci ułamka dziesiętnego w zaokrągleniu do części tysięcznych. Zapisz obliczenia.

\(0{,}984\)

Wykaż, że jeżeli \(a=\log _{2} 14\) oraz \(b=\log _{\sqrt{2}} 27\), to \(\log _{7} 54=\frac{b+2}{2 a-2}\).

Rozważamy wszystkie liczby naturalne sześciocyfrowe, w których zapisie dziesiętnym iloczyn cyfr jest liczbą parzystą mniejszą od \(5\).

Oblicz, ile jest wszystkich takich liczb sześciocyfrowych. Zapisz obliczenia.

\(9\cdot 10^5-9\cdot 9^5+27=368\,586\)

Dany jest prostokąt \(ABCD\), w którym \(|AB|=2 \cdot|A D|\). Na bokach \(AB, BC, CD\) oraz \(DA\) tego prostokąta obrano punkty - odpowiednio - \(K, L, M\) oraz \(N\) (przy czym każdy z tych punktów leży na dokładnie jednym boku prostokąta \(ABCD)\). Czworokąt \(KLMN\) jest trapezem prostokątnym (zobacz rysunek), a wysokość \(LM\) tego trapezu jest równoległa do przekątnej \(BD\) prostokąta.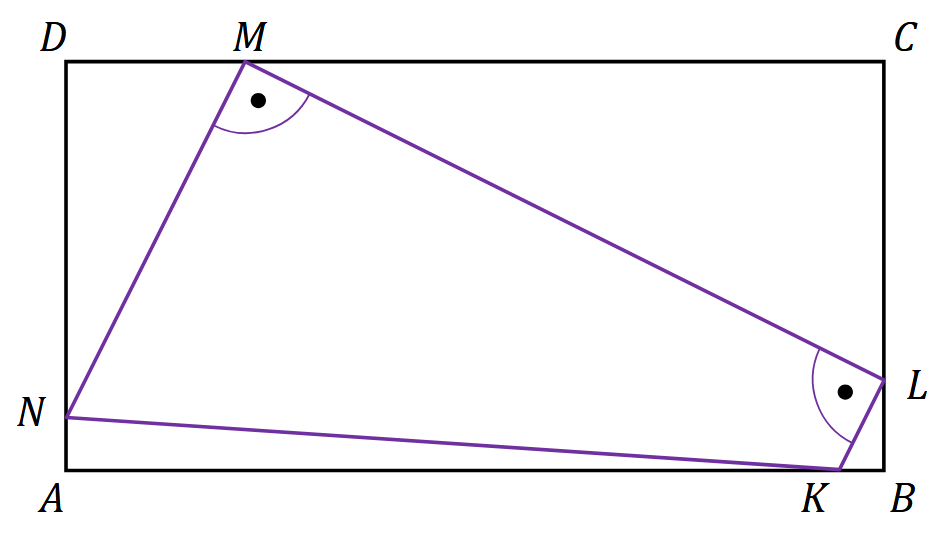

Wykaż, że stosunek pola trójkąta \(MDN\) do pola trójkąta \(KBL\) jest równy \(16\).

Wyznacz wszystkie wartości parametru \(m\), dla których równanie \[ x^{2}+2 m x+2 m-1=0 \] ma dwa różne rozwiązania rzeczywiste \(x_{1}, x_{2}\) spełniające warunek \[ m\left(x_{1}^{2}+x_{2}^{2}\right)=3 m \cdot x_{1} \cdot x_{2}+2 \] Zapisz obliczenia.

\(m=2\)

Rozwiąż równanie \[ \cos (2 x)+2 \cos ^{2}(3 x)+\cos (4 x)=0 \] w przedziale \([0, \pi]\). Zapisz obliczenia.

\(x \in\left\{\frac{\pi}{6}, \frac{\pi}{4}, \frac{\pi}{2}, \frac{3 \pi}{4}, \frac{5 \pi}{6}\right\}\)

Na czworokącie wypukłym \(ABCD\) o bokach długości: \(|AB|=3,|BC|=3,|CD|=5\) oraz \(|DA|=8\), opisano okrąg.

Oblicz promień tego okręgu. Zapisz obliczenia.

\(R=\frac{7\sqrt{3}}{3}\)

Wielomian \(f\) zmiennej rzeczywistej \(x\) jest określony wzorem \(f(x)=x^{3}+a x^{2}+b x+c\), gdzie \(a, b, c \in \mathbb{R}\). Liczba \((-2)\) jest miejscem zerowym tego wielomianu. W kartezjańskim układzie współrzędnych \((x, y)\) styczna do wykresu wielomianu \(f\) w punkcie \(A\) o pierwszej współrzędnej równej \((-2)\) przecina ten wykres w punkcie \(P=(1,9)\).

Wyznacz wzór wielomianu \(\boldsymbol{f}\). Zapisz obliczenia.

Ciąg \(\left(a_{n}\right)\), określony dla każdej liczby naturalnej \(n \geq 1\), jest arytmetyczny i rosnący. W tym ciągu \(a_{6}=15\) oraz \(a_{15}=a_{3} \cdot\left(a_{8}-6\right)\).
Ciąg \(\left(b_{n}\right)\), określony dla każdej liczby naturalnej \(n \geq 1\), jest geometryczny i \(b_{1}=a_{11}\) oraz \(b_{2}=a_{6}\).

Oblicz sumę wszystkich wyrazów ciągu ( \(b_{n}\) ). Zapisz obliczenia.

Dany jest ostrosłup prawidłowy trójkątny \(ABCD\) o podstawie \(ABC\). Płaszczyzna zawierająca krawędź \(AB\) podstawy i prostopadła do krawędzi bocznej \(CD\) przecina tę krawędź w punkcie \(E\), przy czym \(\frac{|CE|}{|DE|}=\frac{3}{11}\).

Oblicz stosunek pola powierzchni całkowitej tego ostrosłupa do pola podstawy \(ABC\). Zapisz obliczenia.

W kartezjańskim układzie współrzędnych ( \(x, y\) ) dany jest równoległobok \(ABCD\) o wierzchołkach \(A=(-8,-1)\) i \(D=(-13,9)\) oraz środku symetrii \(M=\left(-\frac{9}{2}, 1\right)\).
Okrąg \(\mathcal{O}\) przechodzi przez początek tego układu i jest styczny do prostych zawierających boki \(AB\) i \(BC\) tego równoległoboku. Druga współrzędna środka okręgu \(\mathcal{O}\) jest liczbą ujemną.

Wyznacz równanie okręgu \(\mathcal{O}\). Zapisz obliczenia.

Rozważamy wszystkie graniastosłupy prawidłowe trójkątne o polu powierzchni całkowitej równym \(24 \sqrt{3}\).

Wykaż, że objętość \(V\) graniastosłupa w zależności od długości \(a\) krawędzi podstawy jest określona wzorem \[ V(a)=6 a-\frac{1}{8} a^{3} \]

Objętość \(V\) graniastosłupa w zależności od długości a krawędzi podstawy jest określona wzorem \[ V(a)=6 a-\frac{1}{8} a^{3} \] dla \(a \in(0,4 \sqrt{3})\).

Wyznacz długość krawędzi podstawy tego z rozważanych graniastosłupów, którego objętość jest największa. Oblicz tę największą objętość. Zapisz obliczenia.