Matura 2024 sierpień

Drukuj

Poziom podstawowy

Szybka nawigacja do zadania numer: 5 10 15 20 25 30 .

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Liczba wszystkich całkowitych rozwiązań nierówności \(|x+1|\lt3\) jest równa

A.\( 2 \)

B.\( 3 \)

C.\( 5 \)

D.\( 7 \)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Liczba \(\left(\frac{4}{25}\right)^{-0,5}\) jest równa

A.\( 0{,}04 \)

B.\( 0{,}8 \)

C.\( 2{,}5 \)

D.\( 0{,}4 \)

Wykaż, że dla każdej liczby naturalnej \(n \geq 1\) liczba \((2 n+5)^{2}+3\) jest podzielna przez \(4\).

\((2 n+5)^{2}+3=4n^2+20n+25+3=4n^2+20n+28=4(n^2+5n+7)\)

Uzupełnij zdanie. Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A–F i wpisz te litery w wykropkowanych miejscach.

Prawdziwe są równości: ............ oraz ............ .

A.\(\log _{2} 16+\log _{2} 9=\log _{2} 25\)

B.\(\log _{2} 16+\log _{2} 9=2 \cdot \log _{2} 5\)

C.\(\log _{2} 16+\log _{2} 9=\log _{2} 144\)

D.\(\log _{2} 16+\log _{2} 9=\log _{4} 144\)

E.\(\log _{2} 16+\log _{2} 9=4+2 \cdot \log _{2} 3\)

F.\(\log _{2} 16+\log _{2} 9=2 \cdot \log _{4} 12\)

C, E

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Zbiorem wszystkich rozwiązań nierówności \[ \frac{3(6-x)}{17} \leq 3 \] jest przedział

A.\((-\infty,-11)\)

B.\((-\infty,-11]\)

C.\((-11,+\infty)\)

D.\([-11,+\infty)\)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Równanie \(\ \frac{x(x+5)(2-x)}{2 x+4}=0\ \) w zbiorze liczb rzeczywistych ma dokładnie

A.dwa rozwiązania: \((-5)\) oraz 2.

B.dwa rozwiązania: \((-5)\) oraz 0.

C.trzy rozwiązania: \((-5),\ 0\) oraz 2.

D. cztery rozwiązania: \((-5),\ (-2),\ 0\) oraz 2.

Rozwiąż równanie \[ x^{3}+5 x^{2}-2 x-10=0 \] Zapisz obliczenia.

\(x=-5\), \(x=-\sqrt{2}\), \(x=\sqrt{2}\)

Na rysunku, w kartezjańskim układzie współrzędnych \((x, y)\), przedstawiono interpretację geometryczną jednego z poniższych układów równań A-D.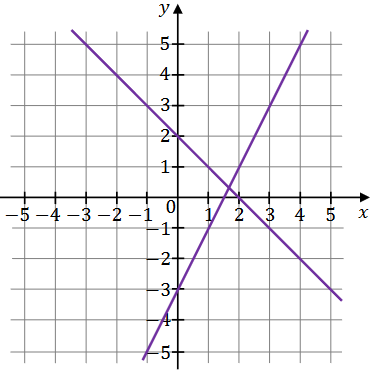

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest

A.\(\left\{\begin{array}{l}y=x+2 \\ y=2 x-3\end{array}\right.\)

B.\(\left\{\begin{array}{l}y=-x+2 \\ y=2 x-3\end{array}\right.\)

C.\(\left\{\begin{array}{l}y=x+2 \\ y=-2 x-3\end{array}\right.\)

D.\(\left\{\begin{array}{l}y=-x+2 \\ y=2 x+3\end{array}\right.\)

Funkcja \(y=f(x)\) jest określona za pomocą tabeli

\(x\)	\(-6\)	\(-4\)	\(-2\)	\(0\)	\(2\)	\(4\)	\(6\)
\(y\)	\(-3\)	\(-4\)	\(4\)	\(1\)	\(5\)	\(0\)	\(2\)

Uzupełnij poniższą tabelę. Wpisz w każdą pustą komórkę tabeli właściwą odpowiedź, wybraną spośród oznaczonych literami A-E.

\(9.1\)	Największa wartość funkcji \(f\) jest równa
\(9.2\)	Miejsce zerowe funkcji \(f\) jest równe

A.\( 1 \)

B.\( 2 \)

C.\( 4 \)

D.\( 5 \)

E.\( 6 \)

\(9.1\ \) D, \(9.2\ \) C

Funkcja liniowa \(f\) jest określona wzorem \(f(x)=\frac{\sqrt{3}}{3} x-3\).

W kartezjańskim układzie współrzędnych \((x, y)\) wykres funkcji \(y=f(x)\) jest prostą nachyloną do osi \(O x\) pod kątem ostrym \(\alpha\).

Uzupełnij poniższe zdanie. Wpisz odpowiednią liczbę w wykropkowanym miejscu tak, aby zdanie było prawdziwe.

Sinus kąta \(\alpha\) jest równy ........... .

\(\frac{1}{2}\)

Pusta bańka na mleko o pojemności \(10\) litrów ma masę \(6,5 \mathrm{~kg}\). Jeden litr mleka ma masę \(1,03 \mathrm{~kg}\).
Niech \(x\) oznacza liczbę litrów mleka w tej bańce, a \(f(x)\) oznacza wyrażoną w kilogramach masę bańki wraz z mlekiem, gdzie \(x \in[0,10]\).

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

Funkcja \(f\) jest malejąca.	P	F
Funkcja \(f\) nie ma miejsc zerowych.	P	F

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Największa wartość funkcji \(f\) jest równa

A.\( 16,8 \)

B.\( 15,8 \)

C.\( 11,3 \)

D.\( 10,3 \)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Funkcja \(f\) jest określona wzorem

A.\(f(x)=6,5 x+1,03\)

B.\(f(x)=1,03 x+10\)

C.\(f(x)=10 x+1,03\)

D.\(f(x)=1,03 x+6,5\)

W kartezjańskim układzie współrzędnych \((x, y)\) przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej \(f\) (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osią \(O x\) układu współrzędnych mają obie współrzędne całkowite.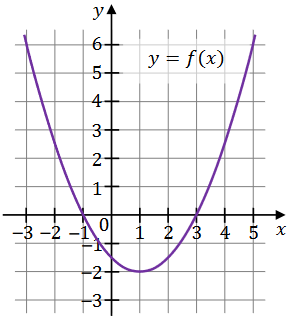

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Zbiorem wartości funkcji \(f\) jest przedział

A.\((-\infty,-2]\)

B.\([1,+\infty)\)

C.\([-1,3]\)

D.\([-2,+\infty)\)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Osią symetrii wykresu funkcji \(f\) jest prosta o równaniu

A.\( x=1 \)

B.\( y=1 \)

C.\( x=-2 \)

D.\( y=-2 \)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Funkcja \(f\) jest określona wzorem

A.\(f(x)=\frac{1}{2}(x-1)^{2}+2\)

B.\(f(x)=\frac{1}{2}(x+1)^{2}+2\)

C.\(f(x)=\frac{1}{2}(x-1)^{2}-2\)

D.\(f(x)=\frac{1}{2}(x+1)^{2}-2\)

Ciąg \(\left(a_{n}\right)\) jest określony dla każdej liczby naturalnej \(n \geq 1\).
Suma \(n\) początkowych wyrazów tego ciągu wyraża się wzorem \(S_{n}=n^{2}+2 n\) dla każdej liczby naturalnej \(n \geq 1\).

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Trzeci wyraz ciągu \(\left(a_{n}\right)\) jest równy

A.\( 5 \)

B.\( 7 \)

C.\( 13 \)

D.\( 15 \)

Dany jest ciąg geometryczny \(\left(a_{n}\right)\) określony dla każdej liczby naturalnej \(n \geq 1\), w którym \(a_{2}=2\) oraz \(a_{5}=54\).

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Iloraz ciągu \(\left(a_{n}\right)\) jest równy

A.\( 3 \)

B.\( 9 \)

C.\( \frac{52}{3} \)

D.\( 27 \)

Trzywyrazowy ciąg ( \(2 m-5,4,9)\) jest arytmetyczny.

Dokończ zdanie. Wybierz odpowiedź A albo B oraz odpowiedź 1., 2. albo 3.

Ten ciąg jest

Kąt \(\alpha\) jest ostry oraz \(\cos \alpha=\frac{24}{25}\).

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Tangens kąta \(\alpha\) jest równy

A.\(\frac{7}{18}\)

B.\( \frac{7}{24} \)

C.\( \frac{7}{25} \)

D.\( \frac{18}{25} \)

W trójkącie prostokątnym \(A B C\) sinus kąta \(C A B\) jest równy \(\frac{3}{5}\), a przeciwprostokątna \(A B\) jest o \(8\) dłuższa od przyprostokątnej \(B C\).

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Długość przeciwprostokątnej \(A B\) tego trójkąta jest równa

A.\( 18 \)

B.\( 20 \)

C.\( 24 \)

D.\( 25 \)

Dany jest trójkąt \(ABC\), w którym \(|AB|=5,|AC|=2\) oraz \(\cos |\sphericalangle BAC|=\frac{3}{5}\).

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Długość boku \(BC\) tego trójkąta jest równa

A.\(\sqrt{17}\)

B.\(\sqrt{23}\)

C.\(\sqrt{35}\)

D.\(\sqrt{41}\)

Punkty \(K, L\) oraz \(M\) leżą na okręgu o środku w punkcie \(S\). Miara kąta \(K S M\) jest równa \(160^{\circ}\) (zobacz rysunek).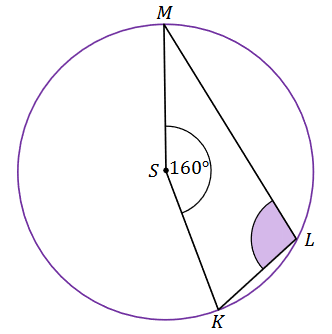

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Miara kąta wpisanego \(K L M\) jest równa

A.\(80^{\circ}\)

B.\(90^{\circ}\)

C.\(100^{\circ}\)

D.\(110^{\circ}\)

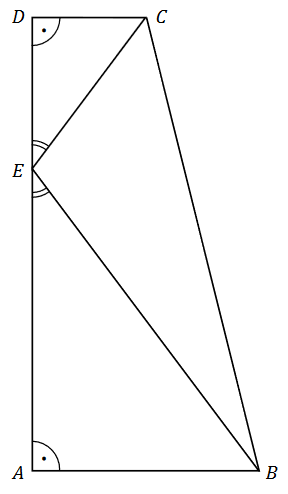
Oblicz długość odcinka \(BE\). Zapisz obliczenia.

\(|BE|=20\)

W kartezjańskim układzie współrzędnych \((x, y)\) przekątne równoległoboku \(ABCD\) przecinają się w punkcie \(S=(9,11)\). Bok \(AB\) tego równoległoboku zawiera się w prostej o równaniu \(y=\frac{1}{2}x-1\), a bok \(AD\) zawiera się w prostej o równaniu \(y=2x-4\).

Oblicz współrzędne wierzchołka \(B\). Zapisz obliczenia.

\(B=(6,2)\)

W kartezjańskim układzie współrzędnych \((x, y)\) proste \(k\) oraz \(l\) są określone równaniami \[ \begin{aligned} & k: y=(3 m-2) x-2 \\ & l: y=(2 m+4) x+2 \end{aligned} \]

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Proste \(k\) oraz \(l\) są równoległe, gdy liczba \(m\) jest równa

A.\( -6 \)

B.\( -6 \)

C.\( 2 \)

D.\( 6 \)

W kartezjańskim układzie współrzędnych \((x, y)\) odcinek o końcach \(A=(-4,7)\) oraz \(B=(6,-1)\) jest średnicą okręgu \(\mathcal{O}\). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Okrąg \(\mathcal{O}\) jest określony równaniem

A.\((x-1)^{2}+(y-3)^{2}=41\)

B.\((x-5)^{2}+(y+4)^{2}=41\)

C.\((x-1)^{2}+(y+3)^{2}=41\)

D.\((x-5)^{2}+(y-4)^{2}=41\)

Liczba wszystkich ścian ostrosłupa prawidłowego jest równa \(12\).

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Liczba wszystkich wierzchołków tego ostrosłupa jest równa

A.\( 10 \)

B.\( 11 \)

C.\( 12 \)

D.\( 13 \)

Długości trzech wychodzących z jednego wierzchołka krawędzi prostopadłościanu są trzema kolejnymi liczbami naturalnymi parzystymi. Najdłuższa krawędź tego prostopadłościanu ma długość \(10\).

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Pole powierzchni całkowitej tego prostopadłościanu jest równe

A.\( 376 \)

B.\( 466 \)

C.\( 480 \)

D.\( 720 \)

Dany jest prostopadłościan \(A B C D E F G H\), w którym podstawy \(A B C D\) i \(E F G H\) są kwadratami o boku długości 6 . Przekątna \(B H\) tego prostopadłościanu tworzy z przekątną \(A H\) ściany bocznej \(A D H E\) kąt o mierze \(30^{\circ}\) (zobacz rysunek).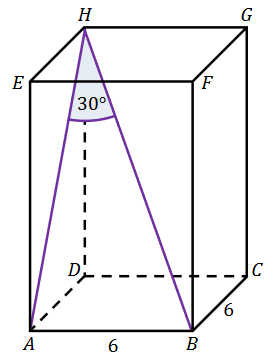

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Przekątna \(BH\) tego prostopadłościanu ma długość równą

A.\( 4 \sqrt{3} \)

B.\( 6 \sqrt{3} \)

C.\( 12 \)

D.\( 12 \sqrt{2} \)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wszystkich liczb naturalnych dwucyfrowych, w których zapisie dziesiętnym cyfra dziesiątek jest o \(3\) większa od cyfry jedności, jest

A.\( 3 \)

B.\( 6 \)

C.\( 7 \)

D.\( 13 \)

W tabeli zestawiono liczbę punktów uzyskanych przez \(32\) uczniów pewnej klasy za rozwiązanie jednego z zadań testu z matematyki.

Liczba punktów	0	1	2	3	4	5
Liczba uczniów	2	2	5	6	11	6

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Średnia arytmetyczna liczby punktów uzyskanych za rozwiązanie tego zadania przez uczniów tej klasy jest równa

A.\( 2,5 \)

B.\( 3,25 \)

C.\( 3,31 \)

D.\( 4 \)

Dane są dwa zbiory: \(C=\{0,4,5,7,9\}\) oraz \(D=\{1,2,3\}\). Losujemy jedną liczbę ze zbioru \(C\), a następnie losujemy jedną liczbę ze zbioru \(D\).

Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że suma wylosowanych liczb będzie większa od 9. Zapisz obliczenia.

\(P(A)=\frac{4}{15}\)

Suma dwóch nieujemnych liczb rzeczywistych \(x\) oraz \(y\) jest równa \(12\).

Wyznacz \(x\) oraz \(y\), dla których wartość wyrażenia \(2 x^{2}+y^{2}\) jest najmniejsza. Oblicz tę najmniejszą wartość. Zapisz obliczenia.

\(x=4\), \(y=8\) \(f(x) = 96\)