Matura podstawowa 2022 - maj
Poziom podstawowy
Pliki do pobrania: Arkusz można też wydrukować w prawym górnym rogu strony według własnych preferencji.
Liczba \((2\sqrt{8}-3\sqrt{2})^2\) jest równa
A.\( 2 \)
B.\( 1 \)
C.\( 26 \)
D.\( 14 \)
Dodatnie liczby \(x\) i \(y\) spełniają warunek \(2x=3y\). Wynika stąd, że wartość wyrażenia \(\frac{x^2+y^2}{x\cdot y}\) jest równa
A.\( \frac{2}{3} \)
B.\( \frac{13}{6} \)
C.\( \frac{6}{13} \)
D.\( \frac{3}{2} \)
Liczba \(4\log_42+2\log_48\) jest równa
A.\( 6\log_410 \)
B.\( 16 \)
C.\( 5 \)
D.\( 6\log_416 \)
Cena działki po kolejnych dwóch obniżkach, za każdym razem o \(10\%\) w odniesieniu do ceny obowiązującej w danym momencie, jest równa \(78\ 732\) zł. Cena tej działki przed obiema obniżkami była, w zaokrągleniu do \(1\) zł, równa
A.\( 98\ 732 \) zł
B.\( 97\ 200\) zł
C.\( 95\ 266\) zł
D.\( 94\ 478\) zł
Liczba \(3^{2+\frac{1}{4}}\) jest równa
A.\( 3^2\cdot \sqrt[4]{3} \)
B.\( \sqrt[4]{3^3} \)
C.\( 3^2+\sqrt[4]{3} \)
D.\( 3^2+\sqrt{3^4} \)
Rozwiązaniem układu równań \begin{cases} 11x-11y=1 \\ 22x+22y=-1 \end{cases} jest para liczb: \(x=x_0\), \(y=y_0\). Wtedy
A.\( x_0\gt 0 \) i \(y_0 \gt 0\)
B.\( x_0\gt 0 \) i \(y_0 \lt 0\)
C.\( x_0\lt 0 \) i \(y_0 \gt 0\)
D.\( x_0\lt 0 \) i \(y_0 \lt 0\)
Zbiorem wszystkich rozwiązań nierówności \(\frac{2}{5}-\frac{x}{3}\gt \frac{x}{5}\) jest przedział
A.\( (-\infty, 0) \)
B.\( (0, +\infty) \)
C.\( \left(-\infty, \frac{3}{4}\right) \)
D.\( \left(\frac{3}{4},+\infty\right) \)
Iloczyn wszystkich rozwiązań równania \(2x(x^2-9)(x+1)=0\) jest równy
A.\( (-3) \)
B.\( 3 \)
C.\( 0 \)
D.\( 9 \)
Na rysunku przedstawiono wykres funkcji \(f\). 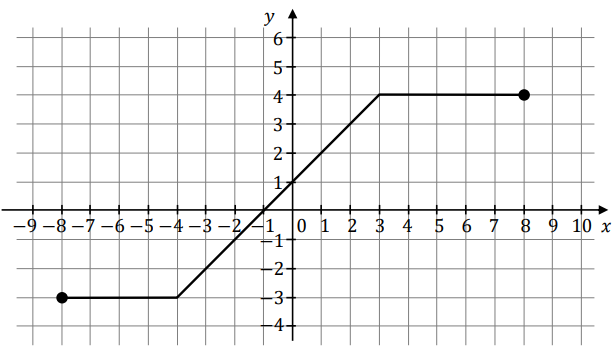 Iloczyn \(f(-3)\cdot f(0)\cdot f(4)\) jest równy
Iloczyn \(f(-3)\cdot f(0)\cdot f(4)\) jest równy
 Iloczyn \(f(-3)\cdot f(0)\cdot f(4)\) jest równy
Iloczyn \(f(-3)\cdot f(0)\cdot f(4)\) jest równy A.\( (-12) \)
B.\( (-8) \)
C.\( 0 \)
D.\( 16 \)
Na rysunku 1. przedstawiono wykres funkcji \(f\) określonej na zbiorze \(\langle -4,5\rangle \). 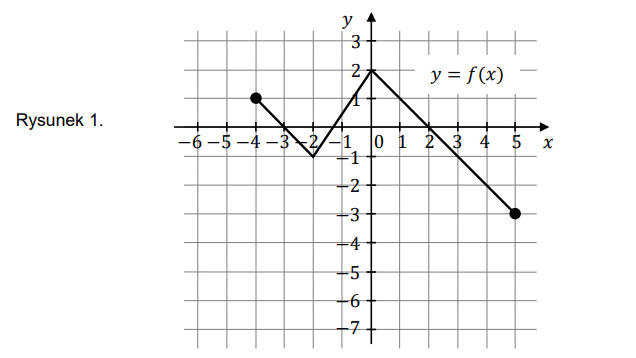 Funkcję \(g\) określono za pomocą funkcji \(f\). Wykres funkcji \(g\) przedstawiono na rysunku 2.
Funkcję \(g\) określono za pomocą funkcji \(f\). Wykres funkcji \(g\) przedstawiono na rysunku 2. 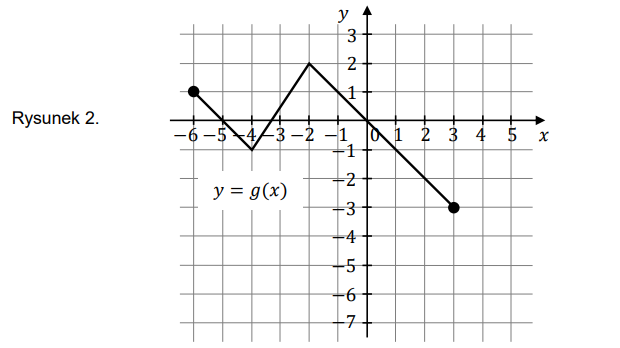 Wynika stąd, że
Wynika stąd, że
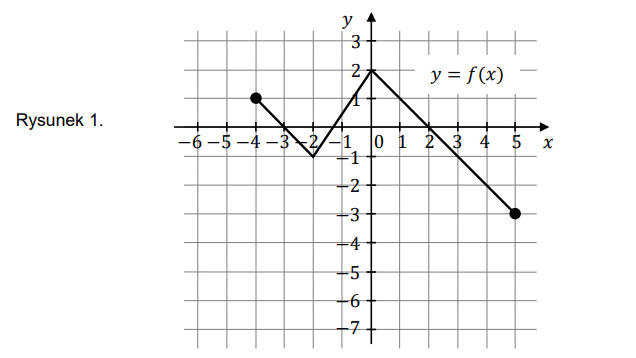 Funkcję \(g\) określono za pomocą funkcji \(f\). Wykres funkcji \(g\) przedstawiono na rysunku 2.
Funkcję \(g\) określono za pomocą funkcji \(f\). Wykres funkcji \(g\) przedstawiono na rysunku 2. 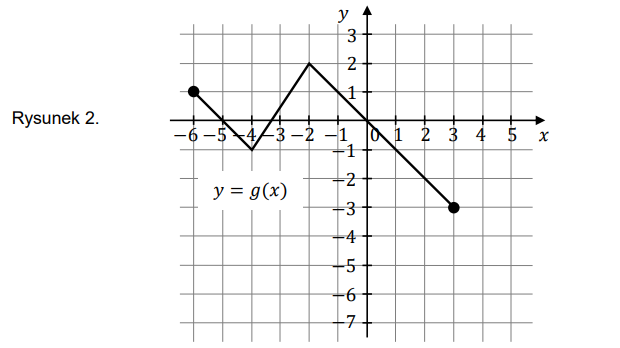 Wynika stąd, że
Wynika stąd, że A.\( g(x)=f(x)-2 \)
B.\( g(x)=f(x-2) \)
C.\( g(x)=f(x)+2 \)
D.\( g(x)=f(x+2) \)
Miejscem zerowym funkcji liniowej \(f\) określonej wzorem \(f(x)=-\frac{1}{3}(x+3)+5\) jest liczba
A.\( (-3) \)
B.\( \frac{9}{2} \)
C.\( 5 \)
D.\( 12 \)
Wykresem funkcji kwadratowej \(f(x)=3x^2+bx+c\) jest parabola o wierzchołku w punkcie \(W=(-3,2)\). Wzór tej funkcji w postaci kanonicznej to
A.\( f(x)=3(x-3)^2+2 \)
B.\( f(x)=3(x+3)^2+2 \)
C.\( f(x)=(x-3)^2+2 \)
D.\( f(x)=(x+3)^2+2 \)
Ciąg \((a_n)\) jest określony wzorem \(a_n=\frac{2n^2-30n}{n}\) dla każdej liczby naturalnej \(n\ge1\). Wtedy \(a_7\) jest równy
A.\( (-196) \)
B.\( (-32) \)
C.\( (-26) \)
D.\( (-16) \)
W ciągu arytmetycznym \((a_n)\), określonym dla każdej liczby naturalnej \(n\ge1\), \(a_5=-31\) oraz \(a_{10}=-66\). Różnica tego ciągu jest równa
A.\( (-7) \)
B.\( (-19{,}4) \)
C.\( 7 \)
D.\( 19{,}4 \)
Wszystkie wyrazy nieskończonego ciągu geometrycznego \((a_n)\), określonego dla każdej liczby naturalnej \(n\ge1\), są dodatnie i \(9a_5=4a_3\). Wtedy iloraz tego ciągu jest równy
A.\( \frac{2}{3} \)
B.\( \frac{3}{2} \)
C.\( \frac{2}{9} \)
D.\( \frac{9}{2} \)
Liczba \(\cos 12^\circ \cdot \sin 78^\circ +\sin 12^\circ \cdot \cos 78^\circ \) jest równa
A.\( \frac{1}{2} \)
B.\( \frac{\sqrt{2}}{2} \)
C.\( \frac{\sqrt{3}}{2} \)
D.\( 1 \)
Punkty \(A,\ B,\ C\) leżą na okręgu o środku \(S\). Punkt \(D\) jest punktem przecięcia cięciwy \(AC\) i średnicy okręgu poprowadzonej z punktu \(B\). Miara kąta \(BSC\) jest równa \(\alpha \), a miara kąta \(ADB\) jest równa \(\gamma \) (zobacz rysunek). 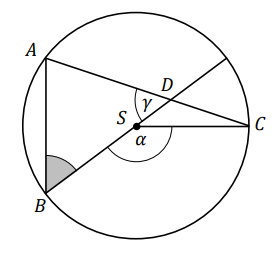 Wtedy kąt \(ABD\) ma miarę
Wtedy kąt \(ABD\) ma miarę
 Wtedy kąt \(ABD\) ma miarę
Wtedy kąt \(ABD\) ma miarę A.\( \frac{\alpha }{2}+\gamma -180^\circ \)
B.\( 180^\circ -\frac{\alpha }{2}-\gamma \)
C.\( 180^\circ -\alpha -\gamma \)
D.\( \alpha +\gamma -180^\circ \)
Punkty \(A,\ B,\ P\) leżą na okręgu o środku \(S\) i promieniu \(6\). Czworokąt \(ASBP\) jest rombem, w którym kąt ostry \(PAS\) ma miarę \(60^\circ \) (zobacz rysunek). 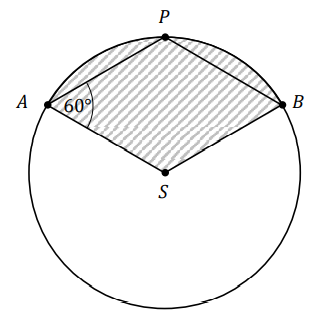 Pole zakreskowanej na rysunku figury jest równe
Pole zakreskowanej na rysunku figury jest równe
 Pole zakreskowanej na rysunku figury jest równe
Pole zakreskowanej na rysunku figury jest równe A.\( 6\pi \)
B.\( 9\pi \)
C.\( 10\pi \)
D.\( 12\pi \)
Wysokość trójkąta równobocznego jest równa \(6\sqrt{3}\). Pole tego trójkąta jest równe
A.\( 3\sqrt{3} \)
B.\( 4\sqrt{3} \)
C.\( 27\sqrt{3} \)
D.\( 36\sqrt{3} \)
Boki równoległoboku mają długości \(6\) i \(10\), a kąt rozwarty między tymi bokami ma miarę \(120^\circ \). Pole tego równoległoboku jest równe
A.\( 30\sqrt{3} \)
B.\( 30 \)
C.\( 60\sqrt{3} \)
D.\( 60 \)
Punkty \(A=(-2,6)\) oraz \(B=(3,b)\) leżą na prostej, która przechodzi przez początek układu współrzędnych. Wtedy \(b\) jest równe
A.\( 9 \)
B.\( (-9) \)
C.\( (-4) \)
D.\( 4 \)
Dane są cztery proste \(k,\ l,\ m,\ n\) o równaniach: \begin{split} &k{:}\ \ y=-x+1\qquad\qquad &l{:}\ \ y=\frac{2}{3}x+1\\[6pt] &m{:}\ \ y=-\frac{3}{2}x+4\qquad\qquad &n{:}\ \ y=-\frac{2}{3}x-1 \end{split} Wśród tych prostych prostopadłe są
A.proste \(k\) oraz \(l\).
B.proste \(k\) oraz \(n\)
C.proste \(l\) oraz \(m\)
D.proste \(m\) oraz \(n\)
Punkty \(K=(4,-10)\) i \(L=(b,2)\) są końcami odcinka \(KL\). Pierwsza współrzędna środka odcinka \(KL\) jest równa \((−12)\). Wynika stąd, że
A.\( b=-28 \)
B.\( b=-14 \)
C.\( b=-24 \)
D.\( b=-10 \)
Punkty \(A=(-4,4)\) i \(B=(4,0)\) są sąsiednimi wierzchołkami kwadratu \(ABCD\). Przekątna tego kwadratu ma długość
A.\( 4\sqrt{10} \)
B.\( 4\sqrt{2} \)
C.\( 4\sqrt{5} \)
D.\( 4\sqrt{7} \)
Podstawą graniastosłupa prostego jest romb o przekątnych długości \(7\) cm i \(10\) cm. Wysokość tego graniastosłupa jest krótsza od dłuższej przekątnej rombu o \(2\) cm. Wtedy objętość graniastosłupa jest równa
A.\( 560\ \text{cm}^3\)
B.\( 280\ \text{cm}^3 \)
C.\( \frac{280}{3}\ \text{cm}^3 \)
D.\( \frac{560}{3}\ \text{cm}^3 \)
Dany jest sześcian \(ABCDEFGH\) o krawędzi długości \(a\). Punkty \(E,\ F,\ G,\ B\) są wierzchołkami ostrosłupa \(EFGB\) (zobacz rysunek). 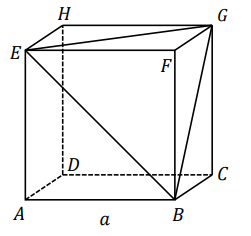 Pole powierzchni całkowitej ostrosłupa \(EFGB\) jest równe
Pole powierzchni całkowitej ostrosłupa \(EFGB\) jest równe
 Pole powierzchni całkowitej ostrosłupa \(EFGB\) jest równe
Pole powierzchni całkowitej ostrosłupa \(EFGB\) jest równe A.\( a^2 \)
B.\( \frac{3\sqrt{3}}{2}a^2 \)
C.\( \frac{3}{2}a^2 \)
D.\( \frac{3+\sqrt{3}}{2}a^2 \)
Wszystkich różnych liczb naturalnych czterocyfrowych nieparzystych podzielnych przez \(5\) jest
A.\( 9\cdot 8\cdot 7\cdot 2 \)
B.\( 9\cdot 10\cdot 10\cdot 1 \)
C.\( 9\cdot 10\cdot 10\cdot 2 \)
D.\( 9\cdot 9\cdot 8\cdot 1 \)
Średnia arytmetyczna zestawu sześciu liczb: \(2x,\ 4,\ 6,\ 8,\ 11,\ 13\) jest równa \(5\). Wynika stąd, że
A.\( x=-1 \)
B.\( x=7 \)
C.\( x=-6 \)
D.\( x=6 \)
Rozwiąż nierówność: \[3x^2-2x-9\ge7\]
W ciągu arytmetycznym \(a_n\), określonym dla każdej liczby naturalnej \(n\ge1\), \(a_1=-1\) i \(a_4=8\). Oblicz sumę stu początkowych kolejnych wyrazów tego ciągu.
Wykaż, że dla każdej liczby rzeczywistej \(a\) i każdej liczby rzeczywistej \(b\) takich, że \(b\ne a\), spełniona jest nierówność \[\frac{a^2+b^2}{2}\gt\left(\frac{a+b}{2}\right)^2\]
Kąt \(\alpha \) jest ostry i \(\operatorname{tg} \alpha =2\). Oblicz wartość wyrażenia \(\sin^{2} \alpha \).
Dany jest trójkąt równoramienny \(ABC\), w którym \(|AC|=|BC|\). Dwusieczna kąta \(BAC\) przecina bok \(BC\) w takim punkcie \(D\), że trójkąty \(ABC\) i \(BDA\) są podobne (zobacz rysunek). Oblicz miarę kąta \(BAC\). 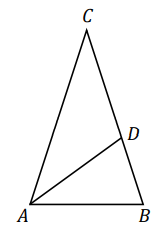

Ze zbioru dziewięcioelementowego \(M=\{1,2,3,4,5,6,7,8,9\}\) losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie \(A\) polega na wylosowaniu dwóch liczb ze zbioru \(M\), których iloczyn jest równy \(24\). Oblicz prawdopodobieństwo zdarzenia \(A\).
Wykres funkcji kwadratowej \(f\) określonej wzorem \(f(x)=ax^2+bx+c\) ma z prostą o równaniu \(y=6\) dokładnie jeden punkt wspólny. Punkty \(A=(-5,0)\) i \(B=(3,0)\) należą do wykresu funkcji \(f\). Oblicz wartości współczynników \(a\), \(b\) oraz \(c\).
Tematy nadrzędne i sąsiednie