Matura podstawowa 2019 - listopad - próbna Operon
Poziom podstawowy
Rozwiązania zadań z matury próbnej Wydawnictwa Operon opublikuję po egzaminie 20 listopada 2019. Arkusz zostanie udostępniony na tej stronie Wydawnictwa.Wartość wyrażenia \((\sqrt{3}-\sqrt{6})^2\) jest równa:
A.\( -3 \)
B.\( 9-6\sqrt{2} \)
C.\( -3-3\sqrt{2} \)
D.\( 3 \)
Zbiorem rozwiązań nierówności \(|x|\le 4\) jest przedział:
A.\( \langle -4,4 \rangle \)
B.\( (-\infty ,4\rangle \)
C.\( (-4,4) \)
D.\( (-\infty ,-4\rangle \cup \langle 4,+\infty ) \)
Liczba \(3\log 2+\log 5^3\) jest równa:
A.\( \log 7^3 \)
B.\( \log 133 \)
C.\( 3\log 7 \)
D.\( 3 \)
Cenę pewnego towaru obniżono dwukrotnie: najpierw o \(20\%\), a następnie o \(10\%\). Końcowa cena tego towaru jest niższa od ceny początkowej o:
A.\( 30\% \)
B.\( 72\% \)
C.\( 28\% \)
D.\( 15\% \)
Suma liczb \(0{,}3(7)\) i \(0{,}(7)\) zapisana w postaci ułamka zwykłego nieskracalnego to:
A.\( \frac{52}{45} \)
B.\( \frac{115555}{100000} \)
C.\( \frac{29}{25} \)
D.\( \frac{23}{20} \)
Funkcja \(f\) przyporządkowuje każdej liczbie naturalnej większej od \(1\) jej największy dzielnik będący liczbą pierwszą. Który zapis jest fałszywy?
A.\( f(22)\gt f(28) \)
B.\( f(21)=f(28) \)
C.\( f(25) \lt 10\)
D.\( f(28)\gt 9 \)
Osią symetrii wykresu funkcji kwadratowej \(f(x)=\frac{1}{7}(x-5)(x+9)\) jest prosta o równaniu:
A.\( x=5 \)
B.\( x=-9 \)
C.\( x=-2 \)
D.\( x=-7 \)
Funkcja liniowa \(f(x)=(m^2-3)x+2\) jest rosnąca wtedy, gdy:
A.\( m \in (-\sqrt{3}, \sqrt{3}) \)
B.\( m \in (-\infty, -\sqrt{3})\cup (\sqrt{3}, \infty ) \)
C.\( m \in \{-\sqrt{3}, \sqrt{3}\} \)
D.\( m \in (\sqrt{3}, \infty ) \)
W trójkącie równoramiennym \(ABC\), w którym \(|AC|=|BC|\) poprowadzono dwusieczne kątów \(ABC\) i \(ACB\). Dwusieczne te przecięły się w punkcie \(O\) (patrz rysunek). Jeśli \(|\sphericalangle BAC|=70^\circ \), to miara kąta \(\alpha \) jest równa: 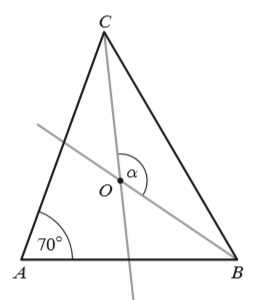

A.\( 140^\circ \)
B.\( 110^\circ \)
C.\( 55^\circ \)
D.\( 125^\circ \)
Pole trapezu jest równe \(20\ \text{cm}^2\), a odcinek łączący środki ramion trapezu ma długość \(4\) cm. Wysokości tego trapezu jest równa:
A.\( 5\ \text{cm}\)
B.\( 10\ \text{cm}\)
C.\( 2{,}5\ \text{cm}\)
D.\( 7{,}5\ \text{cm}\)
Rozwiązaniem równania \((2x-5)(3x+2)=(3x+2)(x+5)\) są liczby:
A.\( -\frac{2}{3} \) i \(10\)
B.\( -5 \) i \(2{,}5\)
C.\( -5 \), \(-\frac{2}{3}\) i \(2{,}5\)
D.\( -5 \) i \(10\)
W trójkącie przedstawionym na rysunku sinus kąta ostrego \(\alpha\) jest równy: 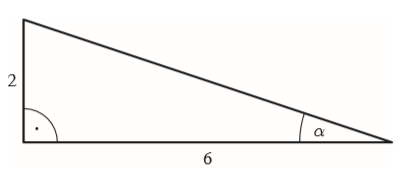

A.\( \frac{1}{3} \)
B.\( 3 \)
C.\( \sqrt{10} \)
D.\( \frac{\sqrt{10}}{10} \)
Funkcja, której wykres przedstawiono na rysunku jest rosnąca: 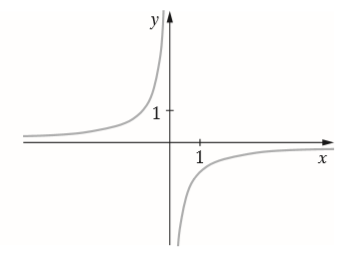

A.tylko w przedziale \( (-\infty ,0) \)
B.tylko w przedziale \( (0,+\infty ) \)
C.w \( \mathbb{R} \backslash \{0\} \)
D.w każdym z przedziałów \( (-\infty ,0) \) i \((0, +\infty )\)
Szósty wyraz ciągu arytmetycznego \((a_n)\) jest równy zero. Suma jedenastu wyrazów tego ciągu ma wartość:
A.\( 0 \)
B.\( 5 \)
C.\( 11 \)
D.\( -11 \)
W ciągu geometrycznym, który ma sześć wyrazów, dane są \(a_3=\frac{1}{2}\) i \(a_6=\frac{1}{16}\). Zatem:
A.\( a_2=\frac{1}{4} \)
B.\( a_2=\frac{1}{8} \)
C.\( a_2=1 \)
D.\( a_2=2 \)
Sześciu robotników wykonało pewną pracę w ciągu \(6\) godzin i \(20\) minut. Ośmiu robotników pracujących z taką samą wydajnością wykona tę samą pracę w ciągu:
A.\(8\) godzin i \(26\) minut
B.\(4\) godzin i \(45\) minut
C.\(4\) godzin i \(20\) minut
D.\(4\) godzin i \(40\) minut
Stosunek obwodów dwóch sześciokątów foremnych wynosi \(\frac{3}{4}\), a długość boku większego z nich jest równa \(12\) cm. Mniejszy sześciokąt foremny ma bok długości:
A.\( 27 \) cm
B.\( 48 \) cm
C.\( 16 \) cm
D.\( 9 \) cm
Funkcję \(f(x)\) przesunięto wzdłuż osi układu współrzędnych, otrzymując funkcję o wzorze \(g(x)=f(x+4)\). Wobec tego funkcję \(f(x)\) przesunięto o:
A.\( 4 \) jednostki w prawo
B.\( 4 \) jednostki w górę
C.\( 4 \) jednostki w lewo
D.\( 4 \) jednostki w dół
Równanie \(\frac{x^2-9}{x-3}=0\):
A.nie ma rozwiązań
B.ma dokładnie jedno rozwiązanie
C.ma dokładnie dwa rozwiązania
D.ma dokładnie trzy rozwiązania
Bok trójkąta równobocznego ma długość \(8\) cm. Odległość środka ciężkości tego trójkąta od jego boków jest równa:
A.\( 2\frac{2}{3} \) cm
B.\( \frac{4\sqrt{3}}{3} \) cm
C.\( \frac{8\sqrt{3}}{3} \) cm
D.\( 4\sqrt{3} \) cm
Mediana uporządkowanego zestawu danych: \(4, 6, a, b, 8, 9\) wynosi \(7{,}5\). Brakującymi wartościami \(a\) i \(b\) mogą być:
A.\( a=6,\ b=6 \)
B.\( a=6,\ b=7 \)
C.\( a=6,\ b=8 \)
D.\( a=7,\ b=8 \)
Przekątna sześcianu ma długość \(6\) cm. Objętość tego sześcianu jest równa:
A.\( 24\sqrt{3}\ \text{cm}^3 \)
B.\( 24\ \text{cm}^3 \)
C.\( 72\sqrt{3}\ \text{cm}^3 \)
D.\( 72\ \text{cm}^3 \)
Kąt rozwarcia stożka jest równy \(30^\circ \), a tworząca tego stożka ma długość \(8\) cm. Pole przekroju osiowego tego stożka wynosi:
A.\( 64\ \text{cm}^2 \)
B.\( 32\ \text{cm}^2 \)
C.\( 16\ \text{cm}^2 \)
D.\( 16\sqrt{3}\ \text{cm}^2 \)
Trzycyfrowy kod aktywacyjny bramy wejściowej ma następującą postać: litera, cyfra, litera. Litera jest wybierana spośród \(24\) liter alfabetu i może się w kodzie powtarzać, a cyfra jest dowolna. Ile różnych kodów można w ten sposób utworzyć?
A.\( 58 \)
B.\( 480 \)
C.\( 5760 \)
D.\( 586 \)
Rzucono \(10\) razy standardową sześcienną kostką do gry. Średnia arytmetyczna liczb oczek uzyskanych w pierwszych \(6\) rzutach była równa \(3{,}5\), a średnia arytmetyczna liczb oczek uzyskanych w kolejnych \(4\) rzutach to \(4{,}5\). Średnia arytmetyczna liczb oczek w \(10\) rzutach wynosi:
A.\( 4{,}1 \)
B.\( 4{,}0 \)
C.\( 3{,}9 \)
D.\( 3{,}8 \)
Rozwiąż nierówność \(2^{13}\cdot x-3\cdot 4^6\lt 8^4(3x-5)\).
Na trójkącie o bokach długości \(\sqrt{5}, \sqrt{15}, \sqrt{10}\) opisano okrąg. Oblicz długość promienia tego okręgu.
Sprawdź, czy punkty \(A=(-2,3)\), \(B=(2,5)\), \(C=(2\sqrt{2},4+\sqrt{2})\) są współliniowe.
Uzasadnij, że równanie \(x^2+(a-1)x-a=0\) dla dowolnej liczby rzeczywistej \(a\) ma przynajmniej jedno rozwiązanie.
Suma długości boku kwadratu i jego przekątnej jest równa \(1\). Oblicz długość przekątnej tego kwadratu. Wynik zapisz w postaci \(a+b\sqrt{c}\).
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że liczba oczek w drugim rzucie jest o dwa większa od liczby oczek w pierwszym rzucie.
Trzy liczby tworzą ciąg arytmetyczny o różnicy \(r=-4\). Jeśli pierwszą i drugą liczbę powiększymy o \(3\), a trzecią powiększymy o \(4\), to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Oblicz liczby tworzące ciąg arytmetyczny i ciąg geometryczny.
Podstawą ostrosłupa \(ABCDE\) jest kwadrat, a spodek \(F\) wysokości \(EF\) ostrosłupa jest środkiem krawędzi \(AD\) (patrz rysunek). Ponadto wiadomo, że każda z dwóch dłuższych krawędzi bocznych tego ostrosłupa ma długość \(12\sqrt{5}\) cm i jest nachylona do płaszczyzny podstawy pod kątem \(60^\circ \). Oblicz objętość tego ostrosłupa. 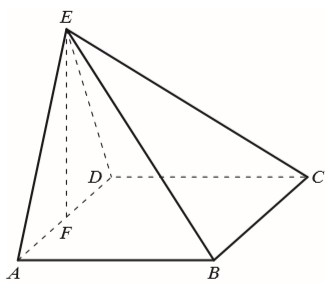

W gospodarstwie ogrodniczym zapakowano \(480\) róż do pewnej liczby kartonów. Gdyby jednak do każdego kartonu włożono o \(3\) róże mniej, to do zapakowania tej samej ilości róż należałoby użyć o \(8\) kartonów więcej. Do ilu kartonów zapakowano pierwotnie róże i ile róż było w każdym kartonie?
Tematy nadrzędne i sąsiednie