Matura rozszerzona 2016 - maj
Poziom rozszerzony
W rozwinięciu wyrażenia \((2\sqrt{3}x+4y)^3\) współczynnik przy iloczynie \(xy^2\) jest równy
A.\( 32\sqrt{3} \)
B.\( 48 \)
C.\( 96\sqrt{3} \)
D.\( 144 \)
Wielomian \(W(x)=6x^3+3x^2-5x+p\) jest podzielny przez dwumian \(x-1\) dla \(p\) równego
A.\( 4 \)
B.\( -2 \)
C.\( 2 \)
D.\( -4 \)
Na rysunku przedstawiono fragment wykresu funkcji homograficznej \(y=f(x)\), której dziedziną jest zbiór \(D=(-\infty ,3)\cup (3,+\infty )\). 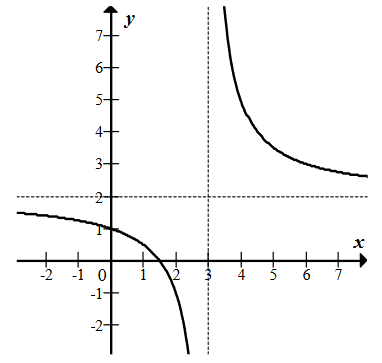 Równanie \(|f(x)|=p\) z niewiadomą \(x\) ma dokładnie jedno rozwiązanie
Równanie \(|f(x)|=p\) z niewiadomą \(x\) ma dokładnie jedno rozwiązanie
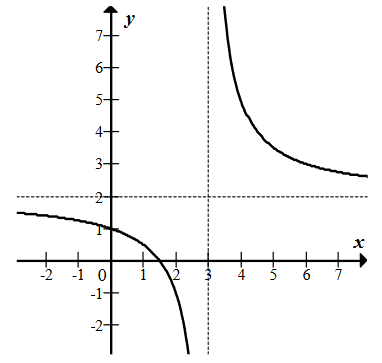 Równanie \(|f(x)|=p\) z niewiadomą \(x\) ma dokładnie jedno rozwiązanie
Równanie \(|f(x)|=p\) z niewiadomą \(x\) ma dokładnie jedno rozwiązanie A.w dwóch przypadkach: \(p=0\) lub \(p=3\).
B.w dwóch przypadkach: \(p=0\) lub \(p=2\).
C.tylko wtedy, gdy \(p=3\).
D.tylko wtedy, gdy \(p=2\).
Funkcja \(f(x)=\frac{3x-1}{x^2+4}\) jest określona dla każdej liczby rzeczywistej \(x\). Pochodna tej funkcji jest określona wzorem
A.\( f'(x)=\frac{-3x^2+2x+12}{(x^2+4)^2} \)
B.\( f'(x)=\frac{-9x^2+2x-12}{(x^2+4)^2} \)
C.\( f'(x)=\frac{3x^2-2x-12}{(x^2+4)^2} \)
D.\( f'(x)=\frac{9x^2-2x+12}{(x^2+4)^2} \)
Granica \(\lim_{n \to \infty} \frac{(pn^2+4n)^3}{5n^6-4n}=-\frac{8}{5}\). Wynika stąd, że
A.\( p=-8 \)
B.\( p=4 \)
C.\( p=2 \)
D.\( p=-2 \)
Wśród \(10\) tysięcy mieszkańców pewnego miasta przeprowadzono sondaż dotyczący budowy przedszkola publicznego. Wyniki sondażu przedstawiono w tabeli.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrana osoba, spośród ankietowanych, popiera budowę przedszkola, jeśli wiadomo, że jest mężczyzną. Zakoduj trzy pierwsze cyfry po przecinku nieskończonego rozwinięcia dziesiętnego otrzymanego wyniku.
| Badane grupy | Liczba osób popierających budowę przedszkola | Liczba osób niepopierających budowy przedszkola |
| Kobiety | 5140 | 1860 |
| Mężczyźni | 2260 | 740 |
Dany jest ciąg geometryczny \((a_n)\) określony wzorem \(a_n=\left(\frac{1}{2x-371}\right )^n\) dla \(n\ge 1\). Wszystkie wyrazy tego ciągu są dodatnie. Wyznacz najmniejszą liczbę całkowitą \(x\), dla której nieskończony szereg \(a_1+a_2+a_3+...\) jest zbieżny.
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych \(x\) i \(y\) takich, że \(x^2+y^2=2\), prawdziwa jest nierówność \(x+y\le 2\).
Dany jest prostokąt \(ABCD\). Okrąg wpisany w trójkąt \(BCD\) jest styczny do przekątnej \(BD\) w punkcie \(N\). Okrąg wpisany w trójkąt \(ABD\) jest styczny do boku \(AD\) w punkcie \(M\), a środek \(S\) tego okręgu leży na odcinku \(MN\), jak na rysunku. 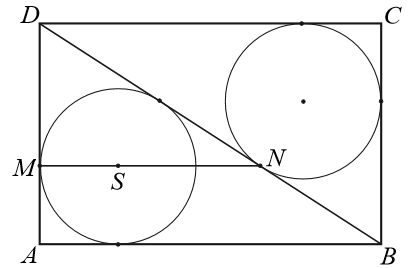 Wykaż, że \(|MN|=|AD|\).
Wykaż, że \(|MN|=|AD|\).
 Wykaż, że \(|MN|=|AD|\).
Wykaż, że \(|MN|=|AD|\).Wyznacz wszystkie wartości parametru \(a\), dla których wykresy funkcji \(f\) i \(g\), określonych wzorami \(f(x)=x-2\) oraz \(g(x)=5-ax\), przecinają się w punkcie o obu współrzędnych dodatnich.
Rozwiąż nierówność \(\frac{2\cos x-\sqrt{3}}{\cos^{2} x}\lt 0\) w przedziale \(\langle 0,2\pi \rangle \).
Dany jest trójmian kwadratowy \(f(x)=x^2+2(m+1)x+6m+1\). Wyznacz wszystkie rzeczywiste wartości parametru \(m\), dla których ten trójmian ma dwa różne pierwiastki \(x_1\), \(x_2\) tego samego znaku, spełniające warunek \(|x_1-x_2|\lt 3\).
Punkty \(A=(30,32)\) i \(B=(0,8)\) są sąsiednimi wierzchołkami czworokąta \(ABCD\) wpisanego w okrąg. Prosta o równaniu \(x-y+2=0\) jest jedyną osią symetrii tego czworokąta i zawiera przekątną \(AC\). Oblicz współrzędne wierzchołków \(C\) i \(D\) tego czworokąta.
Rozpatrujemy wszystkie liczby naturalne dziesięciocyfrowe, w zapisie których mogą występować wyłącznie cyfry \(1\), \(2\), \(3\), przy czym cyfra \(1\) występuje dokładnie trzy razy. Uzasadnij, że takich liczb jest \(15360\).
W ostrosłupie prawidłowym czworokątnym \(ABCDS\) o podstawie \(ABCD\) wysokość jest równa \(5\), a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę \(120^\circ \). Oblicz objętość tego ostrosłupa.
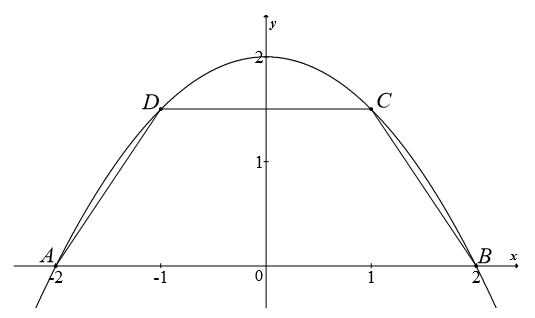
Parabola o równaniu \(y=2-\frac{1}{2}x^2\) przecina oś \(Ox\) układu współrzędnych w punktach \(A=(-2,0)\) i \(B=(2,0)\). Rozpatrujemy wszystkie trapezy równoramienne \(ABCD\), których dłuższą podstawą jest odcinek \(AB\), a końce \(C\) i \(D\) krótszej podstawy leżą na paraboli (zobacz rysunek). Wyznacz pole trapezu \(ABCD\) w zależności od pierwszej współrzędnej wierzchołka \(C\). Oblicz współrzędne wierzchołka \(C\) tego z rozpatrywanych trapezów, którego pole jest największe.