Matura 2012 czerwiec

Drukuj

Poziom podstawowy

Szybka nawigacja do zadania numer: 5 10 15 20 25 30 .

Ułamek \(\frac{\sqrt{5}+2}{\sqrt{5}-2}\) jest równy

A.\( 1 \)

B.\( -1 \)

C.\( 7+4\sqrt{5} \)

D.\( 9+4\sqrt{5} \)

Liczbami spełniającymi równanie \(|2x + 3| = 5\) są

A.\( 1 \) i \(-4\)

B.\( 1 \) i \(2\)

C.\( -1 \) i \(4\)

D.\( -2 \) i \(2\)

Równanie \((x+5)(x-3)(x^2+1)=0\) ma:

A.dwa rozwiązania: \( x=-5, x=3 \)

B.dwa rozwiązania: \( x=-3, x=5 \)

C.cztery rozwiązania: \( x=-5, x=-1, x=1, x=3 \)

D.cztery rozwiązania: \( x=-3, x=-1, x=1, x=5 \)

Marża równa \(1{,}5\%\) kwoty pożyczonego kapitału była równa \(3000\) zł. Wynika stąd, że pożyczono

A.\( 45 \) zł

B.\( 2000 \) zł

C.\( 200\ 000 \) zł

D.\( 450\ 000 \) zł

Na jednym z poniższych rysunków przedstawiono fragment wykresu funkcji \(y=x^2+2x-3\). Wskaż ten rysunek.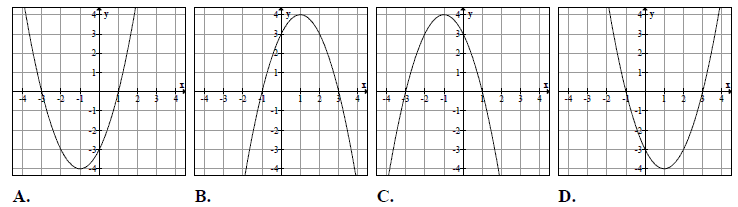

Wierzchołkiem paraboli będącej wykresem funkcji określonej wzorem \(f(x)=x^2-4x+4\) jest punkt o współrzędnych

A.\( (0,2) \)

B.\( (0,-2) \)

C.\( (-2,0) \)

D.\( (2,0) \)

Jeden kąt trójkąta ma miarę \(54^\circ\). Z pozostałych dwóch kątów tego trójkąta jeden jest \(6\) razy większy od drugiego. Miary pozostałych kątów są równe

A.\( 21^\circ \) i \(105^\circ \)

B.\( 11^\circ \) i \(66^\circ \)

C.\( 18^\circ \) i \(108^\circ \)

D.\( 16^\circ \) i \(96^\circ \)

Krótszy bok prostokąta ma długość \(6\). Kąt między przekątną prostokąta i dłuższym bokiem ma miarę \(30^\circ\). Dłuższy bok prostokąta ma długość

A.\( 2\sqrt{3} \)

B.\( 4\sqrt{3} \)

C.\( 6\sqrt{3} \)

D.\( 12 \)

Cięciwa okręgu ma długość \(8\) cm i jest oddalona od jego środka o \(3\) cm. Promień tego okręgu ma długość

A.\( 3 \) cm

B.\( 4 \) cm

C.\( 5 \) cm

D.\( 8 \) cm

Punkt \(O\) jest środkiem okręgu. Kąt wpisany \(BAD\) ma miarę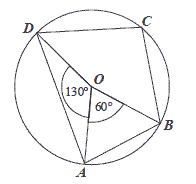

A.\( 150^\circ \)

B.\( 120^\circ \)

C.\( 115^\circ \)

D.\( 85^\circ \)

Pięciokąt \(ABCDE\) jest foremny. Wskaż trójkąt przystający do trójkąta \(ECD\)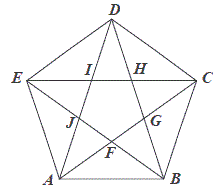

A.\( \Delta ABF \)

B.\( \Delta CAB \)

C.\( \Delta IHD \)

D.\( \Delta ABD \)

Punkt \(O\) jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać: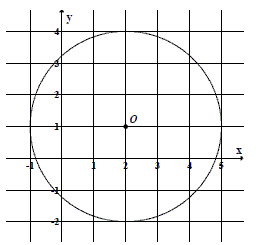

A.\( (x-2)^2+(y-1)^2=9 \)

B.\( (x-2)^2+(y-1)^2=3 \)

C.\( (x+2)^2+(y+1)^2=9 \)

D.\( (x+2)^2+(y+1)^2=3 \)

Wyrażenie \(\frac{3x+1}{x-2}-\frac{2x-1}{x+3}\) jest równe

A.\( \frac{x^2+15x+1}{(x-2)(x+3)} \)

B.\( \frac{x+2}{(x-2)(x+3)} \)

C.\( \frac{x}{(x-2)(x+3)} \)

D.\( \frac{x+2}{-5} \)

Ciąg \((a_n)\) jest określony wzorem \(a_n=\sqrt{2n+4}\) dla \(n\ge 1\). Wówczas

A.\( a_8=2\sqrt{5} \)

B.\( a_8=8 \)

C.\( a_8=5\sqrt{2} \)

D.\( a_8=\sqrt{12} \)

Ciąg \((2\sqrt{2},4,a)\) jest geometryczny. Wówczas

A.\( a=8\sqrt{2} \)

B.\( a=4\sqrt{2} \)

C.\( a=8-2\sqrt{2} \)

D.\( a=8+2\sqrt{2} \)

Kąt \(\alpha \) jest ostry i \(\operatorname{tg} \alpha =1\). Wówczas

A.\( \alpha \lt 30^\circ \)

B.\( \alpha =30^\circ \)

C.\( \alpha =45^\circ \)

D.\( \alpha >45^\circ \)

Wiadomo, że dziedziną funkcji \(f\) określonej wzorem \(f(x)=\frac{x-7}{2x+a}\) jest zbiór \((-\infty ,2)\cup (2,+\infty )\). Wówczas

A.\( a=2 \)

B.\( a=-2 \)

C.\( a=4 \)

D.\( a=-4 \)

Jeden z rysunków przedstawia wykres funkcji liniowej \(f(x)=ax+b\), gdzie \(a>0\) i \(b\lt 0\). Wskaż ten wykres.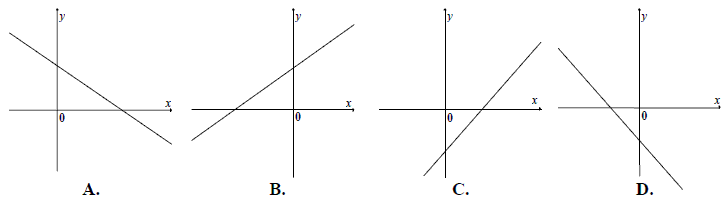

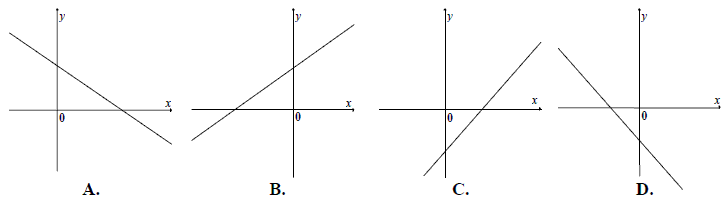
Punkt \(S = (2, 7)\) jest środkiem odcinka \(AB\), w którym \(A = (-1, 3)\). Punkt \(B\) ma współrzędne:

A.\( B=(5,11) \)

B.\( B=\left (\frac{1}{2},2 \right) \)

C.\( B=\left (-\frac{3}{2},-5 \right) \)

D.\( B=(3,11) \)

W kolejnych sześciu rzutach kostką otrzymano następujące wyniki: \(6, 3, 1, 2, 5, 5\). Mediana tych wyników jest równa:

A.\( 3 \)

B.\( 3{,}5 \)

C.\( 4 \)

D.\( 5 \)

Równość \((a+2\sqrt{2})^2=a^2+28\sqrt{2}+8\) zachodzi dla

A.\( a=14 \)

B.\( a=7\sqrt{2} \)

C.\( a=7 \)

D.\( a=2\sqrt{2} \)

Trójkąt prostokątny o przyprostokątnych \(4\) i \(6\) obracamy wokół dłuższej przyprostokątnej. Objętość powstałego stożka jest równa

A.\( 96\pi \)

B.\( 48\pi \)

C.\( 32\pi \)

D.\( 8\pi \)

Jeżeli \(A\) i \(B\) są zdarzeniami losowymi, \(B'\) jest zdarzeniem przeciwnym do \(B\), \(P(A) = 0{,}3\), \(P(B') = 0{,}4\) oraz \(A\cap B=\emptyset \), to \(P(A\cup B)\) jest równe

A.\( 0{,}12 \)

B.\( 0{,}18 \)

C.\( 0{,}6 \)

D.\( 0{,}9 \)

Przekrój osiowy walca jest kwadratem o boku \(a\). Jeżeli \(r\) oznacza promień podstawy walca, \(h\) oznacza wysokość walca, to

A.\( r+h=a \)

B.\( h-r=\frac{a}{2} \)

C.\( r-h=\frac{a}{2} \)

D.\( r^2+h^2=a^2 \)

Rozwiąż nierówność \(x^2 - 3x - 10 \lt 0\).

\(x\in (-2,5)\)

Średnia wieku w pewnej grupie studentów jest równa \(23\) lata. Średnia wieku tych studentów i ich opiekuna jest równa \(24\) lata. Opiekun ma \(39\) lat. Oblicz, ilu studentów jest w tej grupie.

\(15\)

Podstawy trapezu prostokątnego mają długości \(6\) i \(10\) oraz tangens jego kąta ostrego jest równy \(3\). Oblicz pole tego trapezu.

\(P=96\)

Uzasadnij, że jeżeli \(\alpha\) jest kątem ostrym, to \(\sin^4\alpha + \cos^2\alpha = \sin^2\alpha + \cos^4\alpha\).

Uzasadnij, że suma kwadratów trzech kolejnych liczb całkowitych przy dzieleniu przez \(3\) daje resztę \(2\).

Suma \(S_n = a_1 + a_2 + ... + a_n\) początkowych \(n\) wyrazów pewnego ciągu arytmetycznego \((a_n)\) jest określona wzorem \(S_n = n^2 - 2n\). Wyznacz wzór na \(n\)-ty wyraz tego ciągu.

\(a_n=2n-3\)

Dany jest romb, którego kąt ostry ma miarę \(45^\circ\), a jego pole jest równe \(50\sqrt{2}\). Oblicz wysokość tego rombu.

\(h=5\sqrt{2}\)

Punkty \(A = (2,11), B = (8, 23), C = (6,14)\) są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka \(C\) przecina prostą \(AB\) w punkcie \(D\). Oblicz współrzędne punktu \(D\).

\(D=(4,15)\)

Oblicz, ile jest liczb naturalnych pięciocyfrowych, w zapisie których nie występuje zero, jest dokładnie jedna cyfra \(7\) i dokładnie jedna cyfra parzysta.

\(5120\)

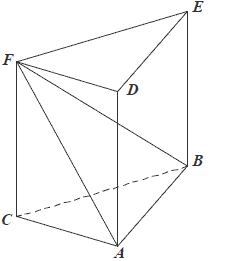
Dany jest graniastosłup prawidłowy trójkątny \(ABCDEF\) o podstawach \(ABC\) i \(DEF\) i krawędziach bocznych \(AD, BE\) i \(CF\) (zobacz rysunek). Długość krawędzi podstawy \(AB\) jest równa \(8\), a pole trójkąta \(ABF\) jest równe \(52\). Oblicz objętość tego graniastosłupa.

\(V=176\sqrt{3}\)