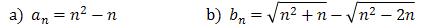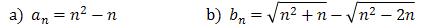Granica ciągu liczbowego
Poziom rozszerzony
Granica ciągu - to liczba do której dążą (są coraz bliżej) kolejne wyrazy ciągu.
Jeżeli ciąg \((a_n)\) ma granicę \(g\), to piszemy tak: \[\lim_{n \to \infty} a_n=g\] Powyższy napis czytamy: "granica ciągu \(a_n\) przy \(n\) dążącym do nieskończoności jest równa \(g\)".
Równoważnie granicę możemy zapisać tak: \[a_n\rightarrow g\ \text{przy}\ n\rightarrow\infty\] co czytamy: "ciąg \(a_n\) dąży do \(g\) przy \(n\) dążącym do nieskończoności".
Jeżeli ciąg \((a_n)\) ma granicę \(g\), to piszemy tak: \[\lim_{n \to \infty} a_n=g\] Powyższy napis czytamy: "granica ciągu \(a_n\) przy \(n\) dążącym do nieskończoności jest równa \(g\)".
Równoważnie granicę możemy zapisać tak: \[a_n\rightarrow g\ \text{przy}\ n\rightarrow\infty\] co czytamy: "ciąg \(a_n\) dąży do \(g\) przy \(n\) dążącym do nieskończoności".
Granica ciągu danego wzorem ogólnym \(a_n=\frac{3n+4}{n}\) jest równa \(3\). Zapiszemy to tak: \[\lim_{n \to \infty} \frac{3n+4}{n}=3\] 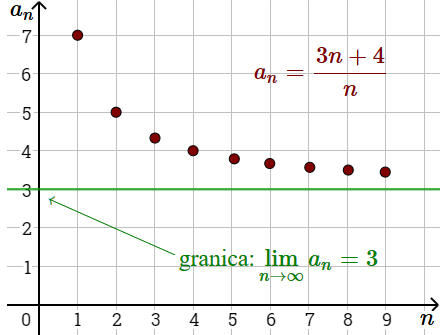

Granica ciągu danego wzorem ogólnym \(a_n=\frac{(-1)^n}{n}\) jest równa \(0\). Zapiszemy to tak: \[\lim_{n \to \infty} \frac{(-1)^n}{n}=0\] 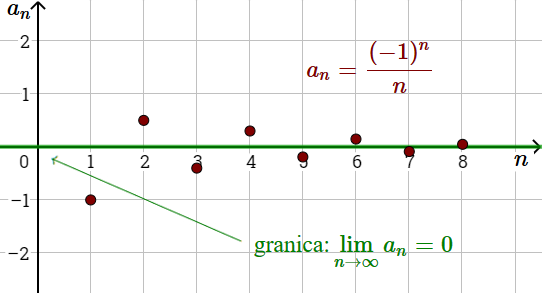

Definicja
Liczba \(g\) jest granicą ciągu (\(a_n\)), jeżeli dla każdego \(\epsilon\gt 0\), istnieje taka liczba \(k\in \mathbb{N} \), że dla wszystkich \(n\gt k\) zachodzi: \[|a_n - g|\lt \epsilon \] Jeżeli ciąg \((a_n)\) ma granicę równą \(g\), to mówimy, że jest zbieżny do \(g\). Pokażemy, korzystając z definicji, że granica ciągu \(a_n=\left(\frac{1}{2}\right)^n\) jest równa \(0\), czyli: \[ \lim_{n \to \infty}\left(\frac{1}{2}\right)^n=0 \] Jeżeli weźmiemy małą liczbę, np. \(\varepsilon=\frac{1}{100}\), to warunek \(\left|\left(\frac{1}{2}\right)^n-0\right|\lt\varepsilon\) jest spełniony, dla wszystkich \(n\ge 7\), ponieważ: \[\left(\frac{1}{2}\right)^7=\frac{1}{128}\lt\frac{1}{100}\] Jeżeli weźmiemy jeszcze mniejszą liczbę, np. \(\varepsilon=\frac{1}{1000}\), to warunek jest spełniony, dla wszystkich \(n\ge 10\).
Dla dowolnie małego \(\varepsilon\) mamy: \[\begin{split} \left|\left(\frac{1}{2}\right)^n-0\right|&\lt\varepsilon\\[6pt] \left(\frac{1}{2}\right)^n&\lt\varepsilon\\[6pt] 2^n&\gt\frac{1}{\varepsilon}\\[6pt] n&\gt\log_2\frac{1}{\varepsilon} \end{split}\] Zatem dla dowolnie małego \(\varepsilon\) istnieje taka liczba naturalna \(k\), że dla wszystkich \(n\gt k\) zachodzi: \(|a_n - 0|\lt \epsilon \).
Taką liczbą \(k\) jest najmniejsza liczba naturalna większa od liczby \(\log_2\frac{1}{\varepsilon}\).
Dla dowolnie małego \(\varepsilon\) mamy: \[\begin{split} \left|\left(\frac{1}{2}\right)^n-0\right|&\lt\varepsilon\\[6pt] \left(\frac{1}{2}\right)^n&\lt\varepsilon\\[6pt] 2^n&\gt\frac{1}{\varepsilon}\\[6pt] n&\gt\log_2\frac{1}{\varepsilon} \end{split}\] Zatem dla dowolnie małego \(\varepsilon\) istnieje taka liczba naturalna \(k\), że dla wszystkich \(n\gt k\) zachodzi: \(|a_n - 0|\lt \epsilon \).
Taką liczbą \(k\) jest najmniejsza liczba naturalna większa od liczby \(\log_2\frac{1}{\varepsilon}\).
Wybrane granice
- Dla \(a \in(-1 ; 1)\): \(\lim _{n \to\infty} a^n=0\)
- Dla \(a \gt 0\): \(\lim_{n \to \infty} \sqrt[n]{a}=1\)
- \(\lim_{n \to\infty}\frac{1}{n}=0\)
- Dla \(a\gt0\): \(\lim _{n \to \infty} \frac{1}{n^a}=0\).
- \(\lim _{n \to\infty} \frac{1}{\sqrt{n}}=0\)
Twierdzenie
Ciąg może mieć tylko jedną granicę.Jeżeli można wskazać dwa podciągi ciągu \((a_n)\), które mają różne granice, to ciąg \((a_n)\) nie ma granicy.
Uzasadnij, że ciąg \(a_n=3\cdot (-1)^n\) nie ma granicy.
Wzór tego ciągu można zapisać również tak: \[a_n=\begin{cases} 3\quad \text{dla}\ n\ \text{parzystych} \\ -3\quad \text{dla}\ n\ \text{nieparzystych} \end{cases} \] Podciąg wyrazów tego ciągu o wyrazach parzystych ma granicę równą \(3\), a podciąg wyrazów o numerach nieparzystych ma granicę równą \(-3\). Zatem ciąg \((a_n)\) nie ma granicy. 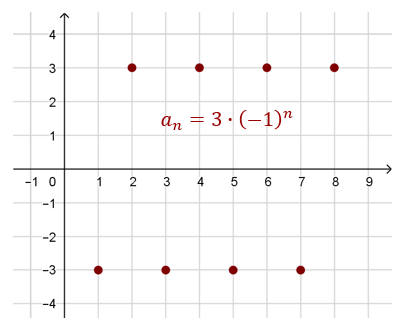

Zbadaj czy istnieje granica ciągu \(a_n=\begin{cases} 1-\frac{1}{n}\quad \text{dla}\ n\ \text{parzystych} \\ 1-\sqrt[n]{2}\quad \text{dla}\ n\ \text{nieparzystych} \end{cases}\).
Podciąg wyrazów tego ciągu o wyrazach parzystych ma granicę równą: \[\lim _{n \to\infty} 1-\frac{1}{n}=1-0=1\] a podciąg wyrazów o numerach nieparzystych ma granicę równą \[\lim _{n \to\infty} 1-\sqrt[n]{2}=1-1=0\] Zatem ciąg \((a_n)\) nie ma granicy.
Oto wykresy obu podciągów: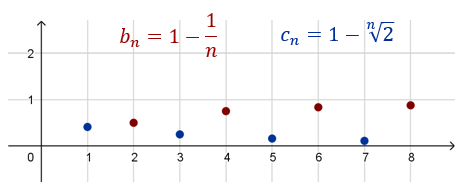
Oto wykresy obu podciągów:

Definicja
Ciąg, który ma granicę nazywamy ciągiem zbieżnym.Ciąg, który nie ma granicy, nazywamy ciągiem rozbieżnym. Jeżeli ciąg jest rozbieżnych do \(+\infty \) lub \(-\infty \), to mówimy, że ma granicę niewłaściwą i piszemy: \[\lim_{n \to \infty} a_n = +\infty\quad \text{lub}\quad \lim_{n \to \infty} a_n = -\infty\]
Ciąg \(a_n=2n-1\) jest rozbieżny do \(+\infty \), czyli ma granicę niewłaściwą: \[\lim_{n \to \infty} 2n-1 = +\infty\] 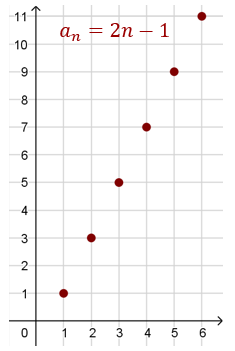

W tym nagraniu wideo przedstawiam intuicję jaka stoi za pojęciem granicy ciągu.
W tym nagraniu wideo omawiam definicję granicy ciągu.
W tym nagraniu pokazuję jak liczyć granice z ciągów niewymiernych.
Czas lekcji: 17 min.
W tym nagraniu omawiam sposoby liczenia granic z ciągów wykładniczych.
Czas lekcji: 20 min.
Oblicz granice ciągów:
\(a_n=\frac{1}{n}+5\)
\(b_n=17-3n\)
\(c_n=\frac{1}{n+3}-7\)
\(d_n=\frac{(-1)^n}{n}\)
Oblicz granice ciągów:
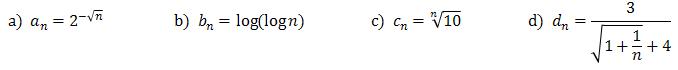
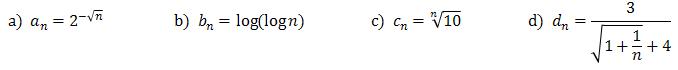
Oblicz granice ciągów:
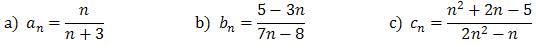
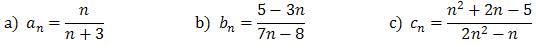
Oblicz granice ciągów:


Oblicz granice ciągów:


Oblicz granice ciągów: