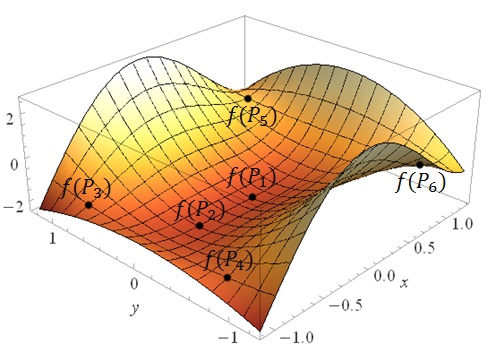
Ekstrema lokalne funkcji dwóch zmiennych - przykład 2
Poziom studiów
Wyznacz ekstrema lokalne funkcji: \[f(x,y)=x^4-3x^2y^2+\frac{2}{3}x^3+3y^2-2\] Rozwiązanie: - Liczymy pochodne cząstkowe pierwszego rzędu: \[\begin{split} f'_{x}&=4x^3-6xy^2+2x^2\\f'_{y}&=-6x^2y+6y \end{split}\]
- Przyrównujemy te pochodne do zera, tworząc układ równań: \[\begin{cases}4x^3-6xy^2+2x^2=0\\-6x^2y+6y=0\end{cases} \]
- Rozwiązujemy powyższy układ równań i wyliczamy punkty stacjonarne: \[\begin{split} \qquad \qquad &\begin{cases}4x^3-6xy^2+2x^2=0\qquad //:2 \\-6x^2y+6y=0\qquad //:(-6) \end{cases}\\[12pt]&\begin{cases}2x^3-3xy^2+x^2=0\\x^2y-y=0\end{cases} \\[12pt]&\begin{cases}2x^3-3xy^2+x^2=0\\y(x^2-1)=0\end{cases} \\[12pt]&\begin{cases}2x^3-3xy^2+x^2=0\\y=0 \lor x=-1 \lor x=1\end{cases} \\[12pt] \end{split}\] Możemy rozbić ten układ na trzy prostsze układy: \[\begin{split} \begin{cases}2x^3-3xy^2+x^2=0\\y=0\end{cases} \quad &\lor \quad \begin{cases}2x^3-3xy^2+x^2=0\\x=-1 \end{cases} \quad &\lor \quad\begin{cases}2x^3-3xy^2+x^2=0\\x=1\end{cases} \\[12pt]\begin{cases}2x^3+x^2=0\\y=0\end{cases} \quad &\lor \quad \begin{cases}-2+3y^2+1=0\\x=-1 \end{cases} \quad &\lor \quad\begin{cases}2-3y^2+1=0\\x=1\end{cases} \\[12pt]\begin{cases}x^2(2x+1)=0\\y=0\end{cases} \quad &\lor \quad \begin{cases}y^2=\frac{1}{3}\\x=-1 \end{cases} \quad &\lor \quad\begin{cases}y^2=1\\x=1\end{cases} \\[12pt]\begin{cases}x=0 \lor x=-\frac{1}{2}\\y=0\end{cases} \quad &\lor \quad \begin{cases}y=\frac{1}{\sqrt{3}} \lor y=-\frac{1}{\sqrt{3}}\\x=-1 \end{cases} \quad &\lor \quad\begin{cases}y=1\lor y=-1\\x=1\end{cases} \end{split}\] Zatem ostatecznie mamy rozwiązania: \[\begin{split} \begin{cases}x=0\\y=0\end{cases} \ &\lor \ \begin{cases}x=-\frac{1}{2}\\y=0\end{cases} \ &\lor \ \begin{cases}x=-1 \\y=\frac{1}{\sqrt{3}}\end{cases} \ &\lor \ \begin{cases}x=-1 \\y=-\frac{1}{\sqrt{3}}\end{cases} \ &\lor \ \begin{cases}x=1\\y=1\end{cases} \ &\lor \ \begin{cases}x=1\\y=-1\end{cases} \end{split}\]
- Wypisujemy punkty stacjonarne: \[\begin{split} &P_{1}=(0,0)\\[6pt]&P_{2}=\left ( -\frac{1}{2},0 \right )\\[6pt]&P_{3}=\left ( -1,\frac{1}{\sqrt{3}} \right )\\[6pt]&P_{4}=\left ( -1,-\frac{1}{\sqrt{3}} \right )\\[6pt]&P_{5}=(1,1)\\[6pt]&P_{6}=(1,-1)\\[6pt] \end{split}\]
- Liczymy pochodne cząstkowe drugiego rzędu.
Zacznijmy od przypomnienia wzorów na pochodne pierwszego rzędu: \[\begin{split} f'_{x}&=4x^3-6xy^2+2x^2\\f'_{y}&=-6x^2y+6y \end{split}\] Dalej liczymy: \[\begin{split} f''_{xx}&=12x^2-6y^2+4x\\f''_{xy}&=-12xy\\f''_{yx}&=-12xy\\f''_{yy}&=-6x^2+6 \end{split}\] - Z otrzymanych pochodnych tworzymy wyznacznik: \[W(x,y)=\begin{vmatrix}12x^2-6y^2+4x & -12xy\\-12xy & -6x^2+6\end{vmatrix} \]
- Obliczamy powyższy wyznacznik kolejno dla wszystkich punktów stacjonarnych: \[W(P_{1})=W(0,0)=\begin{vmatrix}0 & 0\\0 & 6\end{vmatrix} = 0\] \[W(P_{2})=W\left ( -\frac{1}{2},0 \right )=\begin{vmatrix}3-2 & 0\\0 & -\frac{6}{4}+6\end{vmatrix} = \begin{vmatrix}1 & 0\\0 & 4,5\end{vmatrix} = 4,5\] \[W(P_{3})=W\left ( -1,\frac{1}{\sqrt{3}} \right )=\begin{vmatrix}12-2-4 & \frac{12}{\sqrt{3}}\\ \frac{12}{\sqrt{3}} & -6+6\end{vmatrix} = \begin{vmatrix}6 & \frac{12}{\sqrt{3}} \\\frac{12}{\sqrt{3}} & 0\end{vmatrix} = -\frac{144}{3}\] \[W(P_{4})=W\left ( -1,-\frac{1}{\sqrt{3}} \right )=\begin{vmatrix}6 & -\frac{12}{\sqrt{3}} \\-\frac{12}{\sqrt{3}} & 0\end{vmatrix} = -\frac{144}{3}\] \[W(P_{5})=W(1,1)=\begin{vmatrix}10 & -12\\-12 & 0\end{vmatrix} =-144\] \[W(P_{6})=W(1,-1)=\begin{vmatrix}10 & 12\\12 & 0\end{vmatrix} =-144\]
- Sprawdzamy dla każdego punktu stacjonarnego czy istnieje w nim ekstremum: \(W(P_{1})=0\), więc na razie nie wiemy czy w punkcie \(P_{1}\) jest ekstremum.
\(W(P_{2})=4,5>0\), więc w punkcie \(P_{2}\) jest ekstremum.
\(W(P_{3})=-\frac{144}{3}<0\), więc w punkcie \(P_{3}\) nie ma ekstremum.
\(W(P_{4})=-\frac{144}{3}<0\), więc w punkcie \(P_{4}\) nie ma ekstremum.
\(W(P_{5})=-144<0\), więc w punkcie \(P_{5}\) nie ma ekstremum.
\(W(P_{6})=-144<0\), więc w punkcie \(P_{6}\) nie ma ekstremum.
- Wiemy, że funkcja ma ekstremum w punkcie \(P_{2}=\left ( -\frac{1}{2},0 \right )\).
Sprawdzamy czy jest to minimum, czy maksimum.
\(f''_{xx}(P_{2})=1>0\) zatem w punkcie \(P_{2}\) funkcja ma minimum.Obliczymy teraz to minimum korzystając ze wzoru funkcji: \[f(x,y)=x^4-3x^2y^2+\frac{2}{3}x^3+3y^2-2\] Podstawiamy: \[f(P_{2})=f\left ( -\frac{1}{2},0 \right )=\left ( -\frac{1}{2} \right )^4-3\cdot \left ( -\frac{1}{2} \right )^2\cdot 0^2+\frac{2}{3}\left ( -\frac{1}{2} \right )^3+3\cdot 0^2-2=-\frac{97}{48}\] - Sprawdzamy czy istnieje ekstremum w punkcie \(P_{1}=(0,0)\), w którym wyzerował się wyznacznik. Przypomnijmy sobie macierz drugich pochodnych dla tego punktu: \[W(P_{1})=\begin{bmatrix}0 & 0\\0 & 6\end{bmatrix}\] Z tej macierzy odczytujemy, że: \[f''_{yy}=6>0\] Zatem funkcja jednej zmiennej \(f(0,y) \) ma w punkcie \(y=0\) minimum. Zbadamy teraz funkcję jednej zmiennej \(f(x,0)\) w punkcie \(x=0\). Niestety druga pochodna tej funkcji zeruje się (widzimy to z macierzy drugich pochodnych), zatem musimy wyznaczyć jej wzór: \[f(x,0)=x^4+\frac{2}{3}x^3-2\] Sprawdzamy czy funkcja \(f(x,0)\) ma w punkcie \(x=0\) ekstremum. W tym celu badamy pochodną tej funkcji: \[f'(x,0)=4x^3+2x^2=2x^2(2x+1)\]Podsumowując:
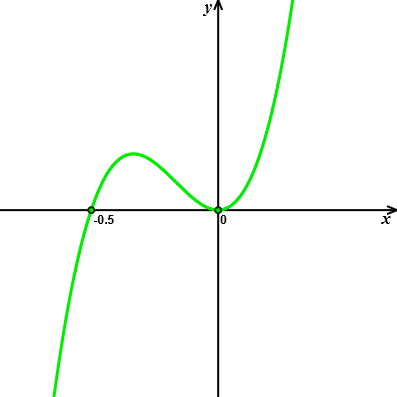Z wykresu pochodnej odczytujemy, że \(f'(x,0)\) nie zmienia znaku w punkcie \(x=0\), zatem funkcja \(f(x,0)\) nie ma w punkcie \(x=0\) ekstremum. Funkcja jednej zmiennej \(f(0,y)\) osiąga w punkcie \(y=0\) ekstremum minimum.
Funkcja jednej zmiennej \(f(x,0)\) w punkcie \(x=0\) nie ma ekstremum.
Zatem funkcja dwóch zmiennych \(f(x,y)\) nie ma ekstremum w punkcie \(P_{1}=(0,0)\).
