Badanie przebiegu zmienności funkcji - przykład 2
Zbadaj przebieg zmienności funkcji: \[ f(x)=\frac{2+\ln x}{x} \]
- Dziedzinę.
- Miejsca zerowe.
- Znajdź granice funkcji \(f\) na krańcach przedziału (przedziałów) określoności.
- Napisz równania wszystkich asymptot.
- Oblicz pochodne pierwszego i drugiego rzędu funkcji \(f\) i wypełnij tabelkę zmienności.
- Naszkicuj część wykresu funkcji \(f\) w kwadracie \(\{(x,y): -1\le x,y\le e\}\).
- Napisz równanie prostej \(p\) stycznej do wykresu funkcji \(f\) w jego punkcie przegięcia.
- Dziedzina.
\(\ln x\) jest określony dla \(x>0\) i dzielimy przez \(x\ne 0\). Zatem \[ \mathcal D=(0,+\infty). \] - Miejsce zerowe.
\[ \frac{2+\ln x}{x}=0 \\[6pt] 2+\ln x=0 \\[6pt] \ln x=-2 \\[6pt] x=e^{-2}. \] - Granice na krańcach dziedziny.
\[ \lim_{x\to 0^+}\frac{2+\ln x}{x}=\left[\frac{-\infty }{0^+}\right]=-\infty, \] oraz: \[ \lim_{x\to+\infty}\frac{2+\ln x}{x} =\lim_{x\to\infty}\Big(\frac{2}{x}+\frac{\ln x}{x}\Big)=0.\] - Asymptota pionowa.
Z dziedziny funkcji: \(x>0\) i granicy w zerze: \(\lim_{x\to 0^+}\frac{2+\ln x}{x}=\left[\frac{-\infty }{0^+}\right]=-\infty\) mamy asymptotę pionową: \[x=0\]Asymptota pozioma (w \(+\infty\)).Brak asymptoty ukośnej.
Z granicy w nieskończoności: \(\lim_{x\to+\infty}\frac{2+\ln x}{x}=0\) mamy asymptotę poziomą: \[y=0\]
Liczymy współczynniki kandydata: \[ a=\lim_{x\to\infty}\frac{f(x)}{x} =\lim_{x\to\infty}\frac{2+\ln x}{x^2}=0 \] Wtedy \[ b=\lim_{x\to\infty}\big(f(x)-ax\big)=\lim_{x\to\infty}f(x)=0. \] Otrzymana prosta to \(y=ax+b\), to \(y=0\) czyli ta sama, co asymptota pozioma. Zatem nie ma osobnej asymptoty ukośnej. - Pochodna i monotoniczność.
\[ f'(x)=\frac{(2+\ln x)'x-(2+\ln x)\cdot 1}{x^2} =\frac{\frac1x\cdot x-(2+\ln x)}{x^2} =-\frac{\ln x+1}{x^2}. \] Zatem \(f'(x)=0 \Leftrightarrow \ln x=-1 \Leftrightarrow x=e^{-1}\).
Ponieważ \(x^2\gt 0\), znak \(f'(x)\) to znak \(-(\ln x+1)\):Przedział \(\ln x+1\) \(f'(x)\) Wniosek \((0,e^{-1})\) \(<0\) \(>0\) funkcja rośnie \(\{e^{-1}\}\) \(=0\) \(=0\) pkt. krytyczny \((e^{-1},\infty)\) \(>0\) \(<0\) funkcja maleje - Ekstrema.
W \(x=e^{-1}\) następuje zmiana z rosnącej na malejącą, więc jest maksimum: \[ f(e^{-1})=\frac{2+\ln(e^{-1})}{e^{-1}}=\frac{2-1}{e^{-1}}=e. \] - Druga pochodna, wklęsłość/wypukłość i przegięcie.
\[ f''(x)=\left(-\frac{\ln x+1}{x^2}\right)'=\frac{2\ln x+1}{x^3}. \] \[ f''(x)=0 \iff 2\ln x+1=0 \iff x=e^{-1/2}. \] Dla \(x\lt e^{-1/2}\) mamy \(f''(x)\lt 0\) (wklęsła), dla \(x\gt e^{-1/2}\) mamy \(f''(x)\gt 0\) (wypukła).
Liczymy wartość: \[f(e^{-1/2})=\frac{2-\tfrac12}{e^{-1/2}}=\tfrac{3}{2}\sqrt e\] Zatem punkt przegięcia: \[ \left(e^{-1/2},\,\tfrac{3}{2}\sqrt e\right). \] -
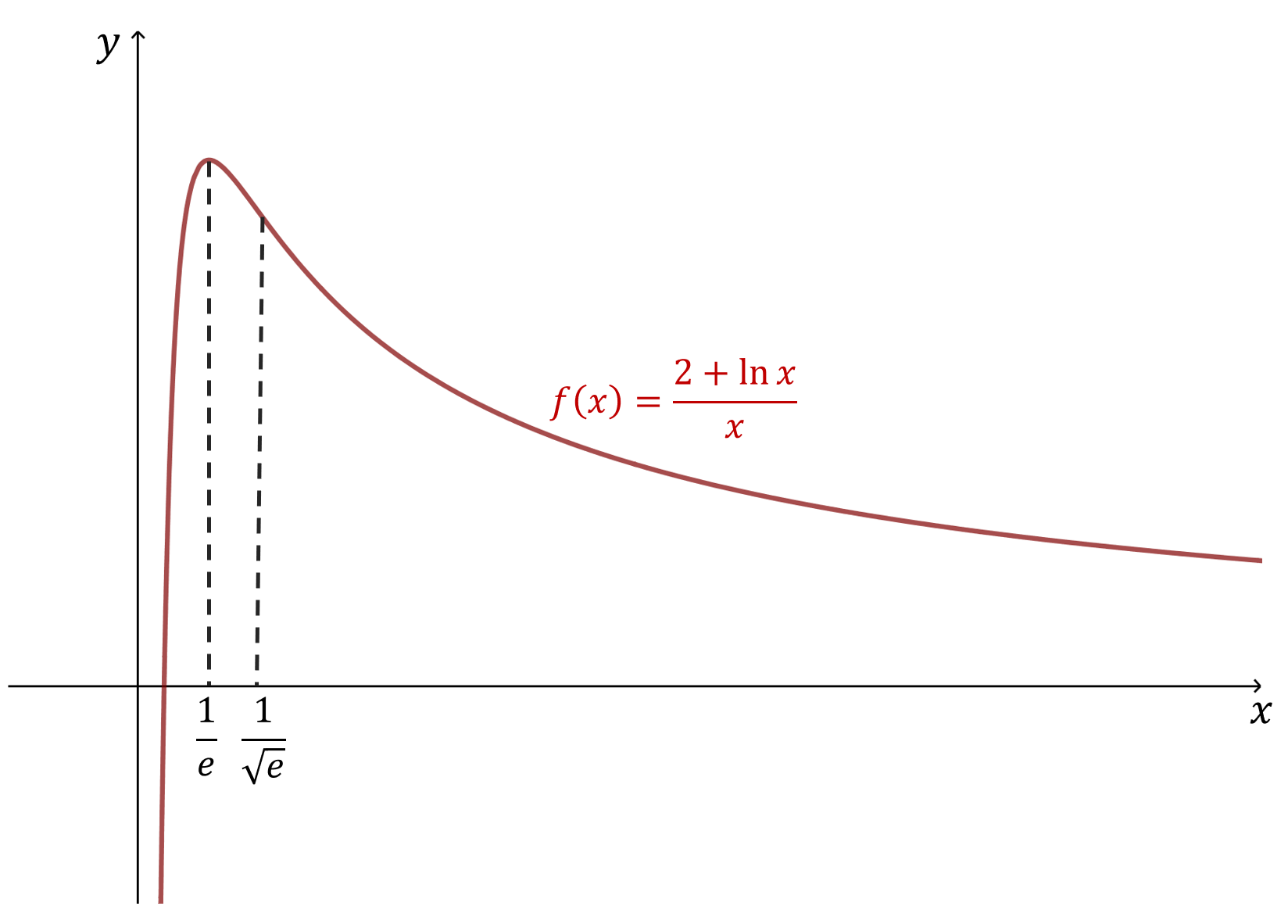
- Styczna w punkcie przegięcia.
Współczynnik kierunkowy prostej: \[ a=f'(e^{-1/2})=-\frac{\ln(e^{-1/2})+1}{(e^{-1/2})^2} =-\frac{-\tfrac12+1}{e^{-1}}=-\frac e2. \] Wyraz wolny prostej: \[b=y_0-mx_0=\tfrac32\sqrt e+\tfrac12\sqrt e=2\sqrt e\] Zatem równanie stycznej to: \[ \boxed{\ y=-\frac e2\,x+2\sqrt e\,}. \]