Arkusz maturalny 1
Poziom podstawowy
Wyrażenie \(\sqrt{1{,}5^2+0{,}8^2}\) jest równe:
A.\( 2{,}89 \)
B.\( 2{,}33 \)
C.\( 1{,}89 \)
D.\( 1{,}70 \)
Ile rozwiązań w zbiorze liczb rzeczywistych ma nierówność: \(|x+3| \le 0\)?
A.\( 0 \)
B.\( 1 \)
C.\( 2 \)
D.nieskończenie wiele
Wielokąt, który ma \(2\) razy mniej przekątnych niż boków, jest:
A.czworokątem
B.pięciokątem
C.sześciokątem
D.siedmiokątem
Liczba \(a\) stanowi \(80\%\) liczby \(b\). Zatem:
A.\( b=1{,}2a \)
B.\( a-b=0{,}2a \)
C.\( a-b=0{,}2b \)
D.\( 8b=10a \)
Na dwóch przeciwległych bokach kwadratu o polu \(P\) zaznaczono punkty \(A\) i \(B\), przy czym punkt \(A\) jest środkiem boku, zaś punkt \(B\) dzieli bok w stosunku \(3:1\), jak na rysunku obok. Pole zamalowanego czworokąta jest równe: 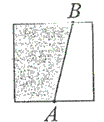

A.\( \frac{2P}{3} \)
B.\( \frac{5P}{8} \)
C.\( \frac{3P}{4} \)
D.\( \frac{3P}{5} \)
Do przedziału \((1, \sqrt{2})\) należy liczba:
A.\( \sqrt{3}-1 \)
B.\( 2\sqrt{5}-3\sqrt{2} \)
C.\( \sqrt{6}-\sqrt{3} \)
D.\( \sqrt{5}-\sqrt{1} \)
Liczbę \(0{,}000421\) można zapisać w postaci \(a\cdot 10^k\), gdzie \(a \in \langle 1, 10 ), k \in \mathbb{Z} \). Wówczas:
A.\( a=0{,}421;\ k=-3 \)
B.\( a=4{,}21;\ k=-5 \)
C.\( a=4{,}21;\ k=-4 \)
D.\( a=42{,}1;\ k=-6 \)
Wiadomo, że \(\log_{0,5}x=−1\). Zatem:
A.\( x=-2 \)
B.\( x=-\frac{1}{2} \)
C.\( x=\frac{1}{2} \)
D.\( x=2 \)
Po usunięciu niewymierności z mianownika \(\frac{2+\sqrt{2}}{2-\sqrt{2}}\) otrzymamy:
A.\( 3+2\sqrt{2} \)
B.\( \frac{2}{(2-\sqrt{2})^2} \)
C.\( 5\sqrt{2} \)
D.\( \frac{(2+\sqrt{2})(2-\sqrt{2})}{2} \)
Dwie funkcje \(f(x)=2x-1\) oraz \(g(x)=-x^2\) określone są w zbiorze \(\mathbb{R}.\) Wówczas wykres funkcji \(h\) określonej wzorem \(h(x)=f(x)+g(x)\) jest przedstawiony na rysunku: 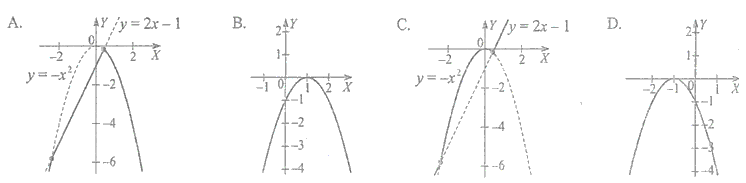

Ile, co najwyżej, liczb naturalnych należy do dziedziny funkcji określonej wzorem \(f(x)=\sqrt{1-x}\)?
A.\( 0 \)
B.\( 1 \)
C.\( 2 \)
D.Nieskończenie wiele
Pewien hurtownik zmieszał \(10\) kg cukierków orzechowych po \(21\) zł za kilogram, \(15\) kg cukierków waniliowych po \(22\) zł za kilogram i \(20\) kg cukierków owocowych po \(18\) zł za kilogram. Pół kilograma takiej mieszanki kosztuje:
A.\( 21 \) zł
B.\( 20 \) zł
C.\( 10{,}50 \) zł
D.\( 10 \) zł
Funkcja liniowa \(f(x)=6-2x\) przyjmuje wartości nieujemne wtedy i tylko wtedy, gdy:
A.\( x\in (-\infty, 3\rangle \)
B.\( x\in \langle 3, +\infty ) \)
C.\( x\in (-\infty, 3) \)
D.\( x\in (3, +\infty ) \)
Funkcja liniowa \(f(x)=(m^2-1)x-7\) jest malejąca, jeśli:
A.\( m\in \mathbb{R} \)
B.\( m\in (-\infty , -1) \)
C.\( m\in (-1, 1) \)
D.\( m\in (-\infty , 0) \)
Suma długości krawędzi sześcianu wynosi \(24\) cm. Pole powierzchni całkowitej tego sześcianu jest równe:
A.\( 32 \) cm2
B.\( 24 \) cm2
C.\( 16 \) cm2
D.\( 8 \) cm2
Wyrażenie \(\frac{x^{-2}+x^{-3}}{x^{-3}-x^{-2}}\), gdzie \(x \ne 0\) i \(x \ne 1\) , po uproszczeniu może mieć postać:
A.\( \frac{x+1}{1-x} \)
B.\( \frac{x-1}{x+1} \)
C.\( \frac{x+2}{x-1} \)
D.\( \frac{1+x}{x} \)
Ze wsi \(A\) do wsi \(B\) prowadzi \(5\) ścieżek przez las. Na ile sposobów można odbyć spacer \(A-B-A\) tak, aby spacer ze wsi \(B\) do wsi \(A\) odbyć inną ścieżką niż ze wsi \(A\) do wsi \(B\)?
A.\( 5^4 \)
B.\( 5+4 \)
C.\( 4^5 \)
D.\( 5\cdot 4 \)
Ogólny wyraz nieskończonego ciągu \((a_n)\), gdzie \(n \in \mathbb{N}_+\), jest następujący: \(a_n=(n^2-2)(n^2-3n)\). Wszystkie miejsca zerowe ciągu \((a_n)\) tworzą zbiór:
A.\( \{-\sqrt{2}, 0, \sqrt{2}, 3\} \)
B.\( \{0, \sqrt{2}, 3\} \)
C.\( \{0, 3\} \)
D.\( \{3\} \)
Pan Jan spłacał kredyt w wysokości \(12\ 000\) zł w sześciu ratach, z których każda kolejna była o \(500\) zł mniejsza od poprzedniej. Pierwsza rata była równa:
A.\( 2750 \)zł
B.\( 3000 \)zł
C.\( 3250 \)zł
D.\( 3500 \)zł
Punkty \(A\) i \(B\) należą do okręgu o środku w punkcie \(O\) i promieniu \(3\). Wiadomo, że \(|\sphericalangle AOB|=150^\circ \). Cięciwa \(AB\) dzieli okrąg na dwa łuki, z których większy ma długość:
A.\( 2{,}5\pi \)
B.\( 3{,}5\pi \)
C.\( 3{,}75\pi \)
D.\( 5{,}25\pi \)
W rombie bok i krótsza przekątna mają taką samą długość, równą \(a\). Wówczas dłuższa przekątna ma długość:
A.\( a\sqrt{2} \)
B.\( a\sqrt{3} \)
C.\( 2a \)
D.\( \frac{a\sqrt{3}}{2} \)
W równoległoboku kąt rozwarty jest cztery razy większy od kąta ostrego \(\alpha\). Zatem:
A.\( \alpha=36^\circ \)
B.\( \alpha=45^\circ \)
C.\( \alpha=60^\circ \)
D.\( \alpha=72^\circ \)
W ostrosłupie prawidłowym czworokątnym krawędź boczna ma długość \(5\) cm, a krawędź podstawy \(\sqrt{8}\) cm. Wówczas cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy jest równy:
A.\( \frac{\sqrt{2}}{5} \)
B.\( 0{,}6 \)
C.\( 0{,}4 \)
D.\( \frac{\sqrt{8}}{10} \)
Rozłóż wielomian \(W(x)=x^4+5x^2-x^3-5x\) na czynniki możliwie najniższego stopnia.
W trójkącie prostokątnym przyprostokątne mają długość \(a\) i \(b\), zaś naprzeciw boku \(a\) znajduje się kąt ostry \(\alpha\). Wykaż, że jeśli \(\operatorname{tg} \alpha = 2,\) to:\[\frac{(a+b)\cdot b}{a^2-b^2}=1\]
Trzy lata temu pewne miasteczko liczyło \(25\ 000\) mieszkańców. Przez trzy ostatnie lata każdego roku liczba mieszkańców zmniejszyła się o \(10\%\). Oblicz, ile osób mieszka w tym miasteczku.
Dane są kwadraty: \(ABCD\) i \(CEFG\) (zobacz rysunek poniżej). Wykaż, że \(|DE|=|BG|\). 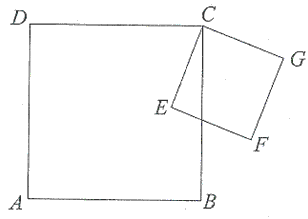

W sklepie wśród dziesięciu żarówek trzy są wadliwe, a pozostałe są dobrej jakości. Klient kupił losowo wybraną jedną żarówkę (bez sprawdzania). Po namyśle dokupił jeszcze jedną. Czy prawdopodobieństwo zdarzenia, że klient, otrzyma obie żarówki dobrej jakości, jest większe od \(0{,}5\)? Odpowiedź uzasadnij, wykonując odpowiednie obliczenia.
Wykres funkcji \(f(x)=x^2-2x-8,\) gdzie \(x \in \mathbb{R}\), przecina oś \(OX\) w punktach \(A\) i \(B\).
- Wyznacz współrzędne punktów \(A\) i \(B\).
- Oblicz pole trójkąta \(AWB\), jeśli \(W\) jest wierzchołkiem paraboli będącej wykresem funkcji \(f\).
Wykaż, że różnica sześcianów dwóch kolejnych liczb nieparzystych jest podzielna przez \(2\) i jednocześnie nie jest podzielna przez \(4\).
Przekątna graniastosłupa prawidłowego czworokątnego \(ABCDA_1B_1C_1D_1\) ma długość \(2\sqrt{219}\), a krawędź podstawy - \(10\sqrt{2}\). 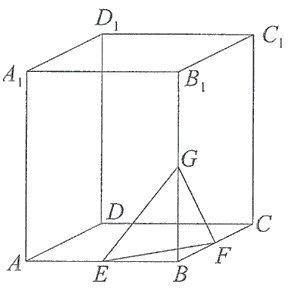 Wyznacz:
Wyznacz:
 Wyznacz:
Wyznacz:- Wysokość graniastosłupa.
- Pole trójkąta \(EFG\), którego wierzchołkami są środki trzech krawędzi wychodzących z jednego wierzchołka podstawy.
Punkty \(A\), \(B\) i \(C\) okręgu dzielą ten okrąg na trzy łuki, których długości pozostają w stosunku \(\overset{\frown}{|AB|}:\overset{\frown}{|BC|}:\overset{\frown}{|AC|}=3:4:5\). Oblicz miary kątów \(\alpha\), \(\beta\), \(\gamma\) trójkąta \(ABC\). 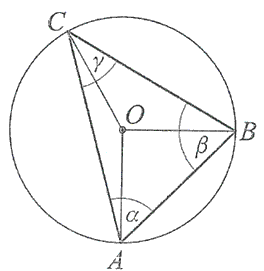

Tematy nadrzędne i sąsiednie