Całki
1.
Wprowadzenie do całekWprowadzenie do całek
Poziom studiów
Całkowanie jest działaniem odwrotnym do różniczkowania.Żeby sprawnie liczyć całki, należy wcześniej dobrze opanować liczenie pochodnych.
Całkę oznaczamy symbolem: \[\int \] Symbol ten pochodzi od łacińskiego słowa Summa (suma).
Całką funkcji \(f(x)\) nazywamy taką funkcję \(F(x)\), że: \[F'(x)=f(x)\] Funkcję \(F(x)\) spełniającą powyższy warunek nazywa się funkcją pierwotną.
Operację całkowania zapisuemy w następujący sposób: \[\int f(x)dx=F(x)\]
Znaczek \(dx\) oznacza, że całkujemy funkcję \(f(x)\) po zmiennej \(x\) (i tak symbolicznie zamyka operację całkowania). Przy liczeniu prostych całek symbol \(dx\) na nic nie wpływa, ale należy go pisać ze względów formalnych.
Możemy zatem napisać, że schemat całkowania wygląda następująco: 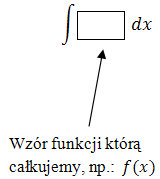
W tym nagraniu omawiam najprostsze całki nieoznaczone. Pokazuję intuicję jaka stoi za pojęciem całki oraz najważniejsze wzory pozwalające liczyć proste całki.
Czas nagrania: 17 min.
Oblicz całkę funkcji \(f(x) = 2x + 7\).
Wykonujemy następujący rachunek: \[\int f(x)\ dx=\int 2x+7\ dx=x^2+7x\] Sprawdzamy rozwiązanie: \[(x^2+7x)'=2x+7\] Należy jednak zauważyć, że znaleziona przez nas funkcja \(F(x) = x^2 + 7x\) nie jest jedynym dobrym rozwiązaniem. Do powyższej funkcji moglibyśmy dodać jeszcze dowolną liczbę i wówczas otrzymalibyśmy inną dobrą funkcję pierwotną dla funkcji \(f(x) = 2x + 7\). Na przykład: \[(x^2+7x+13)'=2x+7\] albo: \[(x^2+7x+100)'=2x+7\]
Zatem teoretycznie powinniśmy napisać: \[\int f(x)\ dx=\int 2x+7\ dx=x^2+7x+C\] gdzie \(C\) - to dowolna liczba rzeczywista.
Oblicz całkę funkcji \(f(x) = x^2\).
Wykonujemy następujący rachunek: \[\int f(x)\ dx=\int x^2\ dx=\frac{1}{3}x^3+C\] Sprawdzamy rozwiązanie: \[\left(\frac{1}{3}x^3+C\right)'=\frac{1}{3}\cdot 3x^2=x^2\]
Do całkowania prostych funkcji wykorzystujemy wzory całkowe, które są również przydatne przy liczeniu całek bardziej skomplikowanych funkcji.
Tematy nadrzędne i sąsiednie