Pochodne
1.
Definicja pochodnej funkcjiDefinicja pochodnej funkcji
Załóżmy, że mamy daną funkcję \(f(x)\) oraz argument \(x_0\), w otoczeniu którego funkcja \(f(x)\) jest określona.
Pochodną funkcji \(f(x)\) w punkcie \(x_0\) oznaczamy symbolem: \[f'(x_0)\] i definiujemy jako granicę: \[f'(x_0)=\lim_{x \to x_0} \frac{f(x)-f(x_0)}{x-x_0}\] Możemy również zdefiniować pochodną jako granicę: \[f'(x_0)=\lim_{h \to 0} \frac{f(x_0+h)-f(x_0)}{h}\]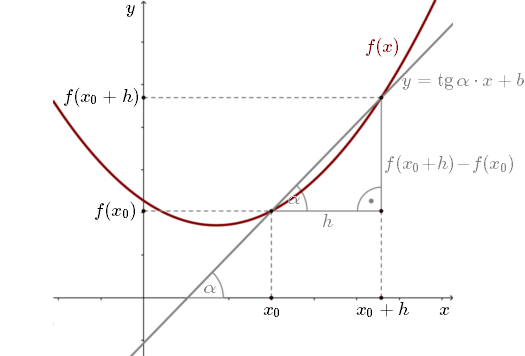 Przez dwa punkty funkcji \(f(x)\) (dla argumentów \(x_0\) oraz \(x_0+h\)) poprowadziliśmy prostą \(y\) daną wzorem: \[y=\operatorname{tg} \alpha \cdot x+b\] gdzie z definicji tangensa w trójkącie prostokątnym mamy: \[\operatorname{tg} \alpha =\frac{f(x_0+h)-f(x_0)}{h}\] Czyli na Rys. 1 iloraz różnicowy, to po prostu współczynnik kierunkowy szarej prostej!
Przez dwa punkty funkcji \(f(x)\) (dla argumentów \(x_0\) oraz \(x_0+h\)) poprowadziliśmy prostą \(y\) daną wzorem: \[y=\operatorname{tg} \alpha \cdot x+b\] gdzie z definicji tangensa w trójkącie prostokątnym mamy: \[\operatorname{tg} \alpha =\frac{f(x_0+h)-f(x_0)}{h}\] Czyli na Rys. 1 iloraz różnicowy, to po prostu współczynnik kierunkowy szarej prostej! 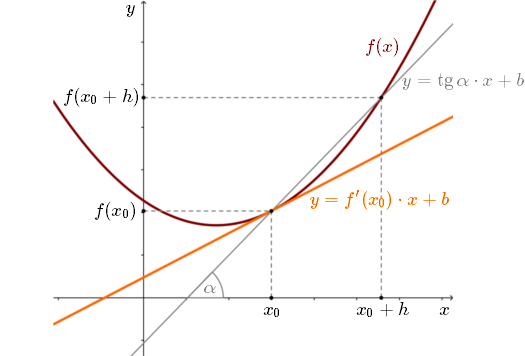 Zauważmy, że jeśli \(h\to 0\), to szara prosta zbiega do pomarańczowej prostej.
Zauważmy, że jeśli \(h\to 0\), to szara prosta zbiega do pomarańczowej prostej.
Możemy wręcz napisać, że: \[\lim_{h \to 0} \operatorname{tg} \alpha = f'(x_0)\] Pochodna pokazuje nam jak funkcja zmienia się w danym punkcie. Dokładniej:
Pochodną funkcji \(f(x)\) w punkcie \(x_0\) oznaczamy symbolem: \[f'(x_0)\] i definiujemy jako granicę: \[f'(x_0)=\lim_{x \to x_0} \frac{f(x)-f(x_0)}{x-x_0}\] Możemy również zdefiniować pochodną jako granicę: \[f'(x_0)=\lim_{h \to 0} \frac{f(x_0+h)-f(x_0)}{h}\]
Obie definicje są równoważne i w zależności od podręcznika, możesz spotkać się z pierwszą lub drugą.
Dalej będę posługiwał się głównie drugą definicją, ponieważ jest częściej spotykana i trochę prostsza w zastosowaniu.
Dalej będę posługiwał się głównie drugą definicją, ponieważ jest częściej spotykana i trochę prostsza w zastosowaniu.
Ułamek z którego liczymy granicę: \(\frac{f(x_0+h)-f(x_0)}{h}\) nazywamy ilorazem różnicowym.
Iloraz różnicowy - to stosunek przyrostu wartości funkcji do przyrostu argumentu funkcji.
Iloraz różnicowy - to stosunek przyrostu wartości funkcji do przyrostu argumentu funkcji.
 Przez dwa punkty funkcji \(f(x)\) (dla argumentów \(x_0\) oraz \(x_0+h\)) poprowadziliśmy prostą \(y\) daną wzorem: \[y=\operatorname{tg} \alpha \cdot x+b\] gdzie z definicji tangensa w trójkącie prostokątnym mamy: \[\operatorname{tg} \alpha =\frac{f(x_0+h)-f(x_0)}{h}\] Czyli na Rys. 1 iloraz różnicowy, to po prostu współczynnik kierunkowy szarej prostej!
Przez dwa punkty funkcji \(f(x)\) (dla argumentów \(x_0\) oraz \(x_0+h\)) poprowadziliśmy prostą \(y\) daną wzorem: \[y=\operatorname{tg} \alpha \cdot x+b\] gdzie z definicji tangensa w trójkącie prostokątnym mamy: \[\operatorname{tg} \alpha =\frac{f(x_0+h)-f(x_0)}{h}\] Czyli na Rys. 1 iloraz różnicowy, to po prostu współczynnik kierunkowy szarej prostej! Interpretacja geometryczna pochodnej
Pochodna funkcji \(f(x)\) w punkcie \(x_0\) - to współczynnik kierunkowy prostej stycznej do \(f(x)\) w punkcie \(x_0\). Zauważmy, że jeśli \(h\to 0\), to szara prosta zbiega do pomarańczowej prostej.
Zauważmy, że jeśli \(h\to 0\), to szara prosta zbiega do pomarańczowej prostej.Możemy wręcz napisać, że: \[\lim_{h \to 0} \operatorname{tg} \alpha = f'(x_0)\] Pochodna pokazuje nam jak funkcja zmienia się w danym punkcie. Dokładniej:
- Jeśli \(f'(x_0)\gt 0\), to funkcja \(f(x)\) rośnie w punkcie \(x_0\).
- Jeśli \(f'(x_0)= 0\), to funkcja \(f(x)\) jest stała w punkcie \(x_0\).
- Jeśli \(f'(x_0)\lt 0\), to funkcja \(f(x)\) maleje w punkcie \(x_0\).
Sposoby oznaczania pochodnych
Pochodną funkcji \(f(x)\) zapisujemy najczęściej tak: \[f'(x)\] Czasami można spotkać się z innymi oznaczeniami:- \(\frac{df(x)}{dx}\) (oznaczenie wprowadzone przez Leibniza)
- \(f'(x)\) (oznaczenie wprowadzone przez Lagrange'a)
- \(Df(x)\) (oznaczenie wprowadzone przez Cauchy'ego)
- \(\frac{dy}{dx}\) (oznaczenie wprowadzone przez Leibniza)
- \(y'\) (oznaczenie wprowadzone przez Lagrange'a)
- \(Dy\) (oznaczenie wprowadzone przez Cauchy'ego)
Pochodne funkcji można liczyć bezpośrednio z definicji, ale dużo łatwiej jest korzystać z gotowych wzorów. Nie musimy wtedy liczyć granicy ilorazu różnicowego, tylko stosujemy proste wzory i reguły liczenia pochodnych.
W poniższych przykładach obliczymy pochodne bezpośrednio z definicji.
Oblicz pochodną funkcji \(f(x) = x^2\) w punkcie \(x_0 = 2\).
Liczymy wartość pochodnej w punkcie \(x_0\) korzystając z definicji: \[ \begin{split} f'(2)&=\lim_{h \to 0} \frac{f(2+h)-f(2)}{h} =\lim_{h \to 0} \frac{(2+h)^2-2^2}{h} =\lim_{h \to 0} \frac{4+4h+h^2-4}{h}\\[6pt] &=\lim_{h \to 0} \frac{4h+h^2}{h} =\lim_{h \to 0} \frac{h(4+h)}{h} =\lim_{h \to 0} (4+h) = 4 \end{split} \] Możemy również policzyć z definicji wzór ogólny pochodnej dla tej funkcji:
\[ \begin{split} f'(x)&=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} =\lim_{h \to 0} \frac{(x+h)^2-x^2}{h} =\lim_{h \to 0} \frac{x^2+2hx+h^2-x^2}{h}\\[6pt] &=\lim_{h \to 0} \frac{2hx+h^2}{h} =\lim_{h \to 0} \frac{h(2x+h)}{h} =\lim_{h \to 0} (2x+h) = 2x \end{split} \] Czyli ostatecznie: \[f'(x)=2x\] Można też napisać równoważnie: \[(x^2)'=2x\] Korzystając z tak wyliczonego wzoru możemy teraz obliczyć wartość pochodnej w dowolnym punkcie, np.: \[ f'(2)=2\cdot 2=4\\[6pt] f'(0)=2\cdot 0=0\\[6pt] f'(-5)=2\cdot (-5)=-10\\[6pt] \] Praktycznie zawsze opłaca się najpierw policzyć pochodną funkcji (zwłaszcza, że mamy do dyspozycji gotowe wzory na liczenie pochodnych), a dopiero potem wyznaczyć jej wartość w konkretnym punkcie.
\[ \begin{split} f'(x)&=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} =\lim_{h \to 0} \frac{(x+h)^2-x^2}{h} =\lim_{h \to 0} \frac{x^2+2hx+h^2-x^2}{h}\\[6pt] &=\lim_{h \to 0} \frac{2hx+h^2}{h} =\lim_{h \to 0} \frac{h(2x+h)}{h} =\lim_{h \to 0} (2x+h) = 2x \end{split} \] Czyli ostatecznie: \[f'(x)=2x\] Można też napisać równoważnie: \[(x^2)'=2x\] Korzystając z tak wyliczonego wzoru możemy teraz obliczyć wartość pochodnej w dowolnym punkcie, np.: \[ f'(2)=2\cdot 2=4\\[6pt] f'(0)=2\cdot 0=0\\[6pt] f'(-5)=2\cdot (-5)=-10\\[6pt] \] Praktycznie zawsze opłaca się najpierw policzyć pochodną funkcji (zwłaszcza, że mamy do dyspozycji gotowe wzory na liczenie pochodnych), a dopiero potem wyznaczyć jej wartość w konkretnym punkcie.
Oblicz pochodną funkcji \(f(x) = x^3 - 2x\).
Liczymy pochodną korzystając z definicji: \[ \begin{split} f'(x)&=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} =\lim_{h \to 0} \frac{\Bigl((x+h)^3-2(x+h)\Bigl)-(x^3-2x)}{h}=\\[6pt] &=\lim_{h \to 0} \frac{x^3+3x^2h+3xh^2+h^3-2x-2h-x^3+2x}{h} =\lim_{h \to 0} \frac{3x^2h+3xh^2+h^3-2h}{h}=\\[6pt] &=\lim_{h \to 0} \frac{h(3x^2+3xh+h^2-2)}{h} =\lim_{h \to 0} (3x^2+3xh+h^2-2)=3x^2-2 \end{split} \] Zatem: \[f'(x)=3x^2-2\] Można napisać równoważnie: \[(x^3 - 2x)'=3x^2-2\]