Zbiór zadań - funkcja kwadratowa
Poziom podstawowy
Zbiorem wartości funkcji \(f(x)=-(x+7)(x-3)\) jest:
A.\( (-\infty ;25\rangle \)
B.\( (-\infty ;-2\rangle \)
C.\( \langle 25;+\infty ) \)
D.\( (-\infty ;2\frac{1}{2}\rangle \)
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej \(f\). Wierzchołkiem tej paraboli jest punkt \(W = (2, -4)\). Liczby \(0\) i \(4\) to miejsca zerowe funkcji \(f\). 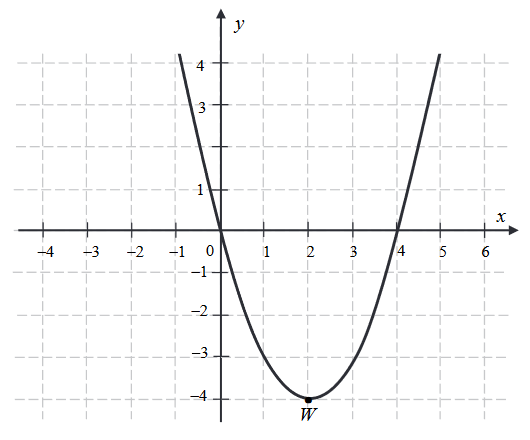 Zbiorem wartości funkcji \(f\) jest przedział
Zbiorem wartości funkcji \(f\) jest przedział
 Zbiorem wartości funkcji \(f\) jest przedział
Zbiorem wartości funkcji \(f\) jest przedział A.\( (-\infty , 0\rangle \)
B.\( \langle 0, 4\rangle \)
C.\( \langle -4, +\infty) \)
D.\( \langle 4, +\infty) \)
Funkcja kwadratowa \(f\) jest określona wzorem \(f(x)=-2(x+3)(x-5)\). Wierzchołek paraboli, która jest wykresem funkcji \(f\), ma współrzędną \(x\) równą
A.\( (-3) \)
B.\( (-1) \)
C.\( 1 \)
D.\( 5 \)
Funkcja \(f\) jest określona wzorem \(f(x)=-x^2+4\) dla każdej liczby rzeczywistej \(x\). Zbiorem wartości funkcji \(f\) jest przedział
A.\( (-\infty, -2\rangle \)
B.\( \langle 2, +\infty) \)
C.\( \langle -4, +\infty) \)
D.\( (-\infty, 4\rangle \)
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej \(f\). 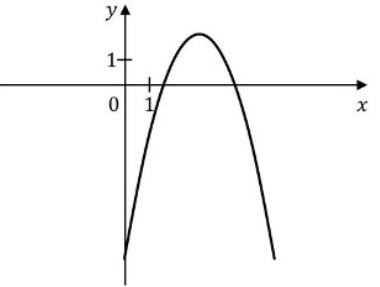 Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji \(f\).
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji \(f\).
 Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji \(f\).
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji \(f\). A.\( f(x)=x^2-6x+11 \)
B.\( f(x)=-x^2+x+2 \)
C.\( f(x)=x^2-6x-7 \)
D.\( f(x)=-x^2+6x-7 \)
W kartezjańskim układzie współrzędnych \((x, y)\) wykresem funkcji kwadratowej \(f\) jest parabola, której wierzchołkiem jest punkt \((3,0)\). Ta parabola przechodzi przez punkt o współrzędnych \((0,-9)\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Funkcja \(f\) jest malejąca w przedziale A.\((-\infty, 0]\)
B.\((-\infty, 3]\)
C.\([0,+\infty)\)
D.\([3,+\infty)\)
Uzupełnij zdanie. Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A-F i wpisz te litery w wykropkowanych miejscach.
Wzór funkcji \(f\) zapisano w odpowiedziach oznaczonych literami: .......... oraz .......... . A.\(f(x)=-x^{2}-9\)
B.\(f(x)=-(x-3)^{2}\)
C.\(f(x)=-(x+3)^{2}\)
D.\(f(x)=-x^{2}+6 x-9\)
E.\(f(x)=-x^{2}-6 x+9\)
F.\(f(x)=-x^{2}-6 x-9\)
Funkcja kwadratowa \(g\) jest określona za pomocą funkcji \(f\) następująco: \(g(x)=f(x)-1\).
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Funkcja \(g\) ma jedno miejsce zerowe. | P | F |
| W kartezjańskim układzie współrzędnych \((x, y)\) osią symetrii wykresu funkcji \(g\) jest prosta o równaniu \(x=3\). | P | F |
Na rysunku są przedstawione fragmenty wykresów funkcji kwadratowych \(f\) i \(g\). Funkcja \(f\) jest określona wzorem \(f(x)=-x^2+6x-5\), a mniejsze z jej miejsc zerowych jest jednocześnie miejscem zerowym funkcji \(g\). Wierzchołek \(W\) paraboli, która jest wykresem funkcji \(f\), leży na wykresie funkcji \(g\), a wierzchołek \(Z\) paraboli będącej wykresem funkcji \(g\) leży na osi \(Oy\) układu współrzędnych. Wyznacz wzór funkcji \(g\). 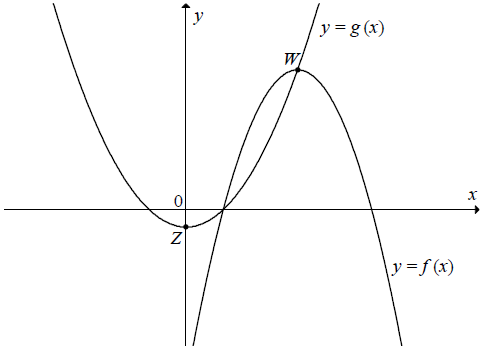
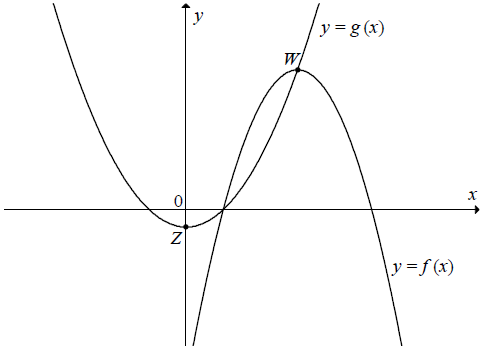
Funkcja kwadratowa \(f\) określona wzorem \(f(x) = −2(x + 1)(x − 3)\) jest malejąca w przedziale
A.\( \langle 1,+\infty ) \)
B.\( (-\infty ,1\rangle \)
C.\( (-\infty ,-8\rangle \)
D.\( \langle -8,+\infty ) \)
Wzór funkcji kwadratowej można zapisać w postaci ogólnej, kanonicznej lub iloczynowej (o ile istnieje).
Dana jest funkcja kwadratowa \(y=f(x)\), której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych \((x,y)\) na rysunku poniżej. 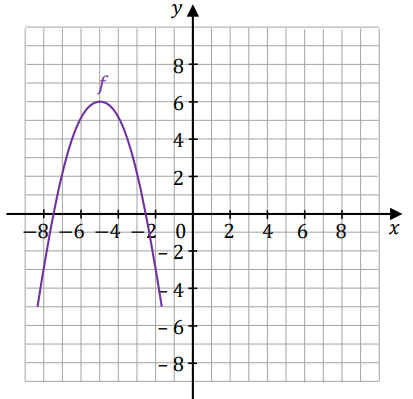

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych, jeżeli wiadomo, że jeden ze wzorów podanych w odpowiedziach A–D to wzór funkcji \(f\).
Funkcja kwadratowa \(y=f(x)\) jest określona wzorem A.\( y=-(x+5)^2-6 \)
B.\( y=-(x+5)^2+6 \)
C.\( y=-(x-5)^2-6 \)
D.\( y=-(x-5)^2+6 \)
Do wykresu pewnej funkcji kwadratowej \(y=g(x)\) należy punkt o współrzędnych \(P=(2,-6)\). Osią symetrii wykresu tej funkcji jest prosta o równaniu \(x=3\), a jednym z miejsc zerowych funkcji \(g\) jest \(x_1=1\).
Wyznacz i zapisz wzór funkcji \(y=g(x)\) w postaci iloczynowej.
Wykresem funkcji kwadratowej \(f(x)=3x^2+bx+c\) jest parabola o wierzchołku w punkcie \(W=(-3,2)\). Wzór tej funkcji w postaci kanonicznej to
A.\( f(x)=3(x-3)^2+2 \)
B.\( f(x)=3(x+3)^2+2 \)
C.\( f(x)=(x-3)^2+2 \)
D.\( f(x)=(x+3)^2+2 \)
Dana jest funkcja kwadratowa \(f\), której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych \((x,y)\) na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji \(f\), oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite. 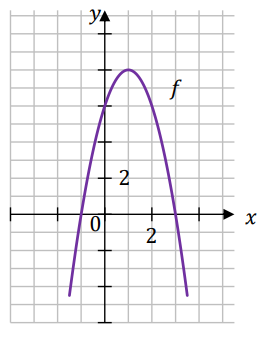

Funkcja \(g\) jest określona za pomocą funkcji \(f\) następująco: \(g(x)=f(x-2)\). 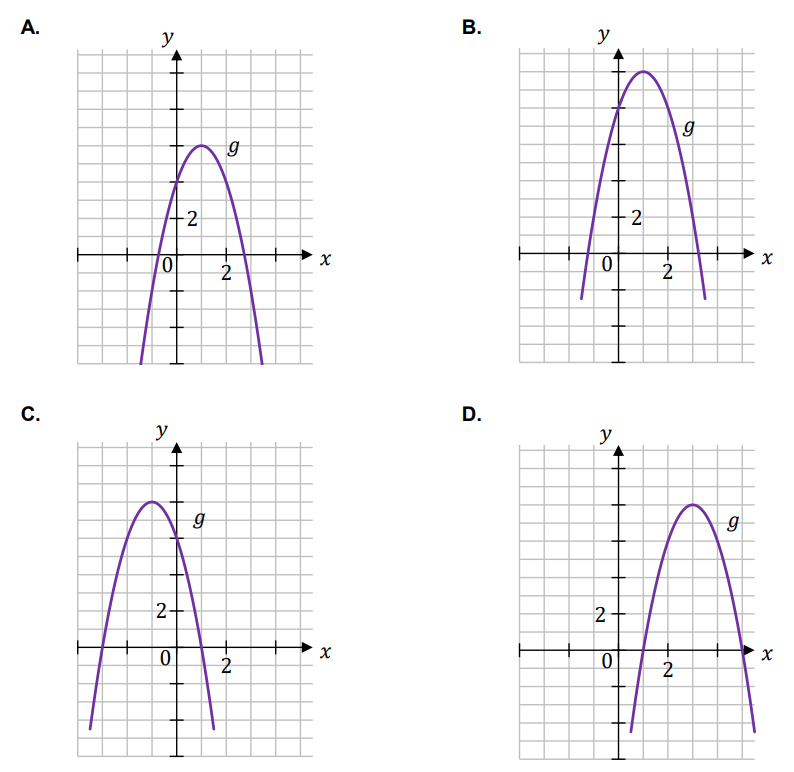
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wykres funkcji \(g\) przedstawiono na rysunku 
Wyznacz i zapisz w miejscu wykropkowanym poniżej zbiór wszystkich rozwiązań nierówności: \[f(x)\le 0\] 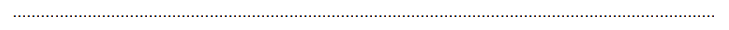
Wyznacz wzór funkcji kwadratowej \(f\) w postaci kanonicznej.
Zapisz obliczenia.
Zapisz obliczenia.
Funkcja kwadratowa \(f\) określona wzorem \(f(x) = x^2 + bx + c\) osiąga dla \(x = 2\) wartość najmniejszą równą \(4\). Wtedy
A.\( b=-4,\ c=8 \)
B.\( b=4,\ c=-8 \)
C.\( b=-4,\ c=-8 \)
D.\( b=4,\ c=8 \)
Dana jest funkcja kwadratowa \(f\) określona wzorem \(f(x) = -2(x - 2)(x + 1)\). Funkcja \(f\) jest rosnąca w zbiorze
A.\( \left(-\infty, \frac{1}{2}\right\rangle \)
B.\( (-1,2) \)
C.\( \left(0, \frac{5}{2}\right) \)
D.\( \left\langle \frac{5}{2}, +\infty \right\rangle \)
Dana jest funkcja \(f\) określona wzorem \(f(x)=x^2-b-2 \sqrt{2}\) dla każdej liczby rzeczywistej \(x\). Miejscem zerowym funkcji \(f\) jest \(x=\sqrt{2}+1\).
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Współczynnik \(b\) we wzorze funkcji \(f\) jest równy A.\((-3)\)
B.\(3\)
C.\(3-\sqrt{2}\)
D.\(3-2 \sqrt{2}\)
Funkcja kwadratowa \(f\) jest określona wzorem \(f(x)=3 x^{2}+2 x+m\) dla każdej liczby rzeczywistej \(x\). Współczynnik \(m\) jest liczbą rzeczywistą mniejszą od zera. 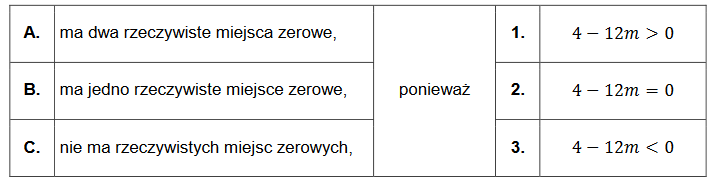
Dokończ zdanie. Zaznacz odpowiedź A, B albo C oraz jej uzasadnienie 1., 2. albo 3.
Funkcja \(f\) 
Wykresem funkcji kwadratowej \(f\) określonej wzorem \(f(x)=x^2+bx+c\) jest parabola, na której leży punkt \(A=(0,-5)\). Osią symetrii tej paraboli jest prosta o równaniu \(x=7\). Oblicz wartości współczynników \(b\) i \(c\).
Dana jest funkcja \(f(x)=-3x^2+bx+c\) dla \(x\in \mathbb{R} \). Prosta o równaniu \(x=2\) jest osią symetrii paraboli będącej jej wykresem, a zbiorem wartości funkcji \(f\) jest przedział \((-\infty ;21\rangle \). Wyznacz współczynniki \(b\) i \(c\).
Funkcja kwadratowa \(f(x)=x^2+bx+c\) nie ma miejsc zerowych. Wykaż, że \(1+c\gt b\).
Wykres funkcji kwadratowej \(f\) określonej wzorem \(f(x)=ax^2+bx+c\) ma z prostą o równaniu \(y=6\) dokładnie jeden punkt wspólny. Punkty \(A=(-5,0)\) i \(B=(3,0)\) należą do wykresu funkcji \(f\). Oblicz wartości współczynników \(a\), \(b\) oraz \(c\).
Oblicz najmniejszą i największą wartość funkcji kwadratowej \(f(x)=x^2-6x+3\) w przedziale \(\langle 0,4\rangle \).
Największa wartość funkcji kwadratowej \(f(x)=a(x-2)^2-4\), gdzie \(a\ne 0\), w przedziale domkniętym \(\langle -4,-2\rangle \) jest równa \(12\). Wyznacz najmniejszą wartość funkcji \(f\) w przedziale \(\langle -4,-2\rangle \).
Funkcja kwadratowa \(f\) przyjmuje w przedziale \(\langle 0,3\rangle \) największą wartość dla argumentów \(0\) i \(3\). Uzasadnij, że w przedziale \(\langle -2,5\rangle \) funkcja \(f\) przyjmuje największą wartość dla argumentów \(-2\) i \(5\).
Funkcja kwadratowa \(f\) jest określona dla wszystkich liczb rzeczywistych \(x\) wzorem \(f(x)=ax^2+bx+c.\) Największa wartość funkcji \(f\) jest równa \(6\) oraz \(f(-6)=f(0)=\frac{3}{2}\). Oblicz wartość współczynnika \(a\).
Funkcja \(f(x)=(m+3)x^2+16x+5\) osiąga wartość największą dla \(x=2\). Oznacza to, że największa wartość tej funkcji jest równa:
A.\( -7 \)
B.\( -14 \)
C.\( 14 \)
D.\( 21 \)
Największą wartością funkcji \(y = -(x-2)^2 + 4\) w przedziale \(\langle 3, 5\rangle\) jest
A.\( 0 \)
B.\( 5 \)
C.\( 4 \)
D.\( 3 \)
Najmniejszą wartością funkcji \(f(x) = (1-x)(x-5)\) w przedziale \(\langle -1, 5\rangle\) jest
A.\( 6 \)
B.\( 0 \)
C.\( -6 \)
D.\( -12 \)
Zadania optymalizacyjne
Producent latarek przeanalizował wpływ zmiany ceny latarki L25 na liczbę kupujących ten produkt. Z analizy wynika, że roczny zysk \(Z\) ze sprzedaży latarek L25 wyraża się wzorem \[ Z(x)=(500+50 x)(16-x) \] gdzie:
\(x\) - kwota obniżki ceny latarki L25 (wyrażona w pełnych złotych), spełniająca warunki \(x \geq 1\) i \(x \leq 14\),
\(Z\) - roczny zysk ze sprzedaży latarek L25 (wyrażony w złotych), liczony od momentu obniżenia ceny.
\(x\) - kwota obniżki ceny latarki L25 (wyrażona w pełnych złotych), spełniająca warunki \(x \geq 1\) i \(x \leq 14\),
\(Z\) - roczny zysk ze sprzedaży latarek L25 (wyrażony w złotych), liczony od momentu obniżenia ceny.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Roczny zysk \(Z\) ze sprzedaży latarek L25 będzie największy dla \(x\) równego A.\(3\)
B.\(4\)
C.\(7\)
D.\(14\)
Hotel ma do dyspozycji gości \(80\) pokoi jednoosobowych. Właściciel hotelu przeanalizował wpływ ceny za dobę hotelową na liczbę wynajętych pokoi i stwierdził, że:
- przy wyjściowej cenie wynoszącej \(120\) zł za jedną dobę hotelową wszystkie pokoje są wynajęte
- każdy wzrost ceny za dobę hotelową o \(5\) zł skutkuje spadkiem liczby wynajmowanych pokoi o \(1\).
Oblicz, jaka powinna być cena wynajęcia jednoosobowego pokoju (za dobę hotelową), aby dobowy przychód hotelu z wynajmowania pokoi był największy. Zapisz obliczenia.
Właściciel pewnej apteki przeanalizował dane dotyczące liczby obsługiwanych klientów z \(30\) kolejnych dni. Przyjmijmy, że liczbę \(L\) obsługiwanych klientów \(n\)-tego dnia opisuje funkcja \[L(n) = -n^2 + 22n + 279\] gdzie \(n\) jest liczbą naturalną spełniającą warunki \(n \ge 1\) i \(n \le 30\).
Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. | Łączna liczba klientów obsłużonych w czasie wszystkich analizowanych dni jest równa \(L(30)\). | P | F |
| W trzecim dniu analizowanego okresu obsłużono \(336\) klientów. | P | F |
Którego dnia analizowanego okresu w aptece obsłużono największą liczbę klientów? Oblicz liczbę klientów obsłużonych tego dnia. Zapisz obliczenia.
Zakład stolarski produkuje krzesła, które sprzedaje po \(196\) złotych za sztukę. Właściciel, na podstawie analizy rzeczywistych wpływów i wydatków, stwierdził, że:
- przychód \(P\) (w złotych) ze sprzedaży \(x\) krzeseł można opisać funkcją \(P(x) = 196x\)
- koszt \(K\) (w złotych) produkcji \(x\) krzeseł dziennie można opisać funkcją \[K(x) = 4x^2 + 4x + 240\]
Wskazówka: przyjmij, że zysk jest różnicą przychodu i kosztów.
Powierzchnia magazynowa będzie się składała z dwóch identycznych prostokątnych działek połączonych wspólnym bokiem. Całość ma być ogrodzona płotem, przy czym obie działki będzie rozdzielał wspólny płot. W ogrodzeniu będą zamontowane dwie bramy wjazdowe, każda o szerokości \(10\) m (zobacz rysunek poniżej). Łączna długość płotu ogradzającego oraz rozdzielającego obie działki wyniesie \(580\) metrów, przy czym szerokości obu bram wjazdowych nie wliczają się w długość płotu. 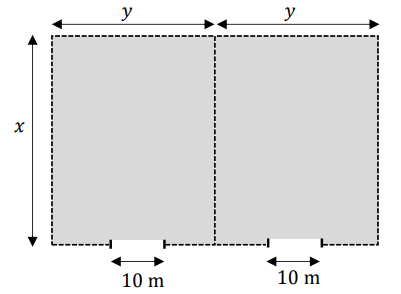

Oblicz wymiary \(x\) i \(y\) każdej z dwóch prostokątnych działek, tak aby całkowite pole powierzchni magazynowej było największe.
Rozważamy wszystkie równoległoboki o obwodzie równym \(200\) i kącie ostrym o mierze \(30^\circ\).
Podaj wzór i dziedzinę funkcji opisującej zależność pola takiego równoległoboku od długości \(x\) boku równoległoboku.
Oblicz wymiary tego z rozważanych równoległoboków, który ma największe pole, i oblicz to największe pole.
Zapisz obliczenia
Oblicz wymiary tego z rozważanych równoległoboków, który ma największe pole, i oblicz to największe pole.
Zapisz obliczenia
Działka ma kształt trapezu. Podstawy \(AB\) i \(CD\) tego trapezu mają długości \(|AB| = 400\) m oraz \(|CD| = 100\) m. Wysokość trapezu jest równa \(75\) m, a jego kąty \(DAB\) i \(ABC\) są ostre.
Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie \(AB\) tego trapezu, a dwa pozostałe - \(E\) oraz \(F\) - na ramionach \(AD\) i \(BC\) trapezu (zobacz rysunek).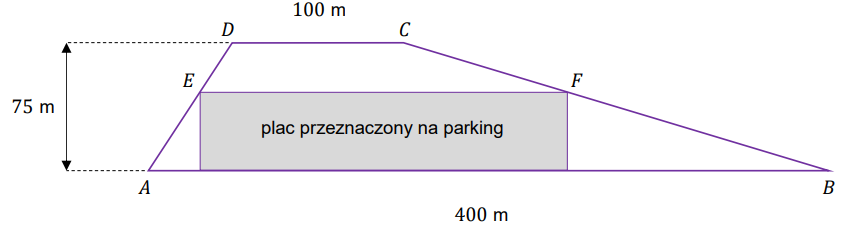
Aby powiązać ze sobą wymiary prostokąta, skorzystaj z tego, że pole trapezu \(ABCD\) jest sumą pól trapezów \(ABFE\) oraz \(EFCD\): \[P_{ABCD}=P_{ABFE}+P_{EFCD}\]
Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie \(AB\) tego trapezu, a dwa pozostałe - \(E\) oraz \(F\) - na ramionach \(AD\) i \(BC\) trapezu (zobacz rysunek).

Wyznacz długości boków prostokąta, dla których powierzchnia wydzielonego placu będzie największa. Wyznacz tę największą powierzchnię. Zapisz obliczenia.
Wskazówka:Aby powiązać ze sobą wymiary prostokąta, skorzystaj z tego, że pole trapezu \(ABCD\) jest sumą pól trapezów \(ABFE\) oraz \(EFCD\): \[P_{ABCD}=P_{ABFE}+P_{EFCD}\]
Rozważamy wszystkie prostopadłościany \(ABCDEFGH\), w których krawędź \(AE\) jest \(3\) razy dłuższa od krawędzi \(A B\), a suma długości wszystkich dwunastu krawędzi prostopadłościanu jest równa \(48\) (zobacz rysunek). Niech \(P(x)\) oznacza funkcję pola powierzchni całkowitej takiego prostopadłościanu w zależności od długości \(x\) krawędzi \(AB\). 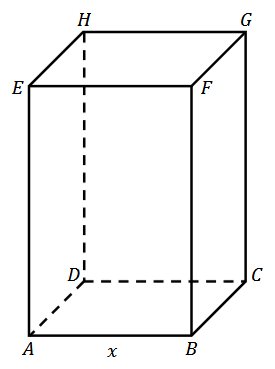

Wyznacz wzór i dziedzinę funkcji \(P\). Oblicz długość \(x\) krawędzi \(AB\) tego z rozważanych prostopadłościanów, którego pole powierzchni całkowitej jest największe. Zapisz obliczenia.
Rozważamy wszystkie prostopadłościany \(A B C D E F G H\), w których krawędź \(BC\) ma długość \(4\) oraz suma długości wszystkich krawędzi wychodzących z wierzchołka \(B\) jest równa \(15\) (zobacz rysunek). 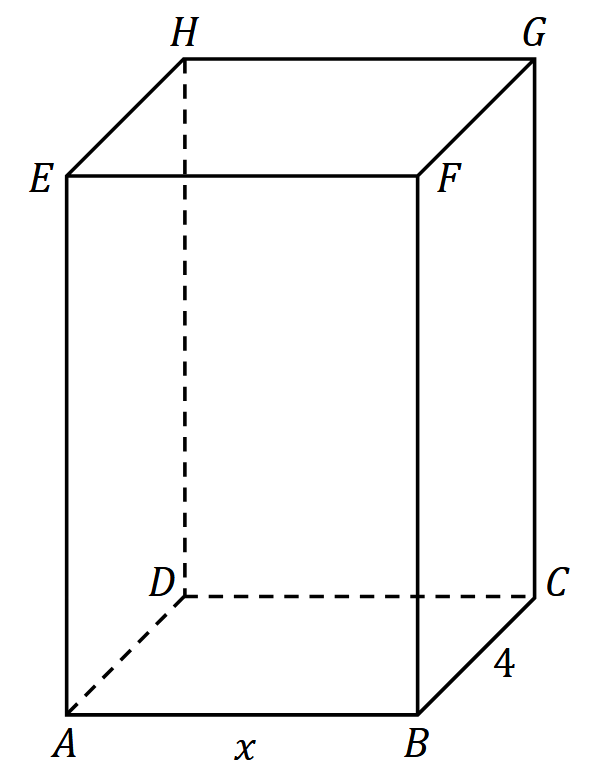 Niech \(P(x)\) oznacza funkcję pola powierzchni całkowitej takiego prostopadłościanu w zależności od długości \(x\) krawędzi \(AB\).
Niech \(P(x)\) oznacza funkcję pola powierzchni całkowitej takiego prostopadłościanu w zależności od długości \(x\) krawędzi \(AB\).
 Niech \(P(x)\) oznacza funkcję pola powierzchni całkowitej takiego prostopadłościanu w zależności od długości \(x\) krawędzi \(AB\).
Niech \(P(x)\) oznacza funkcję pola powierzchni całkowitej takiego prostopadłościanu w zależności od długości \(x\) krawędzi \(AB\). Wyznacz wzór i dziedzinę funkcji \(P\). Oblicz długość \(x\) krawędzi \(AB\) tego z rozważanych prostopadłościanów, którego pole powierzchni całkowitej jest największe. Zapisz obliczenia.
Tematy nadrzędne