Dwa okręgi o promieniach \(r = 2\) i \(R = 6\) są styczne zewnętrznie i są styczne do wspólnej prostej \(k\). Wykaż, że prosta \(l\) przechodząca przez środki \(S\) i \(P\) tych okręgów przecina prostą \(k\) pod kątem \(\alpha = 30^\circ \) (zobacz rysunek). 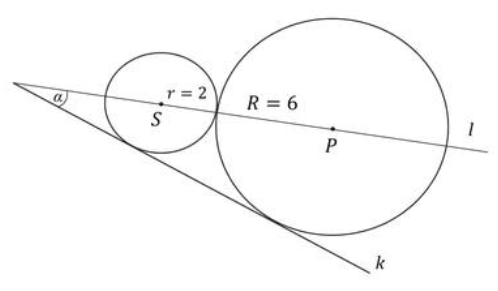

Strony z tym zadaniem
Matura 2020 sierpieńMatura podstawowa - zbiór zadań - promienie, cięciwy i średnice w okręguSąsiednie zadania
Zadanie 3277Zadanie 3278Zadanie 3279 (tu jesteś)
Zadanie 3280Zadanie 3281