Do wzoru funkcji \(f(x) =\sqrt{x}\) nie możemy podstawić pod \(x\)-a liczby ujemnej, ponieważ nie istnieją pierwiastki z liczb ujemnych. Ta funkcja jest określona tylko dla liczb dodatnich oraz zera.

\(x\)	\(-3\)	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)	\(3\)
\(f(x)=\sqrt{x}\)	nie istnieje	nie istnieje	nie istnieje	\(0\)	\(1\)	\(\sqrt{2}\)	\(\sqrt{3}\)

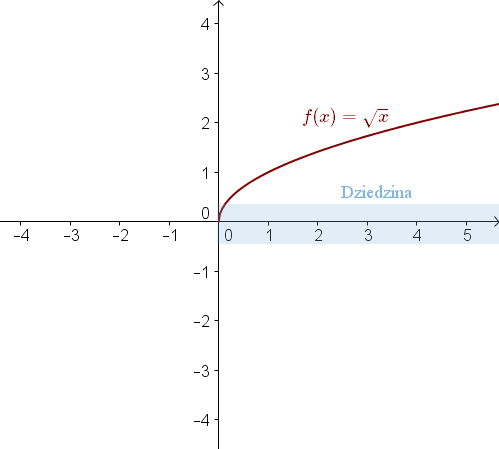
Wykres tej funkcji istnieje tylko dla \(x\)-ów nieujemnych: Dziedzina: \(x\in \langle 0; +\infty )\).
Poniżej podaję inny sposób zapisania tej samej dziedziny.
Dziedzina: \(x\ge 0\).