Różne zadania z funkcji
Dana jest funkcja \(f(x)=\frac{x^2+2}{1-b}\). Oblicz współczynnik \(b\) jeżeli wiadomo, że \(f(2) = -3\).
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{2x-b}{x-9}\) dla \(x \ne 9\). Ponadto wiemy, że \(f(4)=-1\). Oblicz współczynnik \(b\).
Funkcja liniowa \(f(x)=(m+2)x+2m\) jest rosnąca, gdy
A.\( m<-2 \)
B.\( m\lt 2 \)
C.\( m>-2 \)
D.\( m>-4 \)
Punkt \(P=(a+1,2)\) należy do wykresu funkcji \(f(x)=\frac{4}{x}\). Liczba \(a\) jest równa
A.\( 0 \)
B.\( -1 \)
C.\( 2 \)
D.\( 1 \)
Na rysunku przedstawiono wykres funkcji \(f\).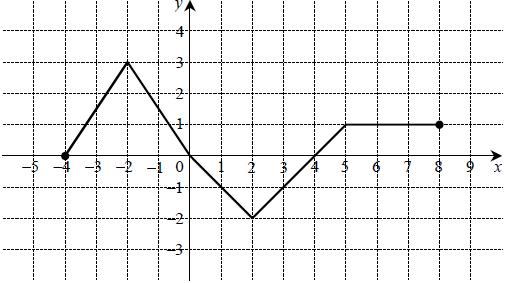 
Odczytaj z wykresu i zapisz:
Odczytaj z wykresu i zapisz: - zbiór wartości funkcji \(f\),
- przedział maksymalnej długości, w którym \(f\) jest malejąca.
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{2x}{x-1}\) dla \(x\ne 1\). Wartość funkcji \(f\) dla argumentu \(x=2\) jest równa
A.\( 2 \)
B.\( -4 \)
C.\( 4 \)
D.\( -2 \)
Dana jest funkcja \(h(x)=\left ( -\frac{1}{3}m+2 \right)x+\frac{3}{2}m-1\). Funkcja ta dla argumentu \(0\) przyjmuje wartość \(5\). Wówczas:
A.\( m=9 \)
B.\( m=6 \)
C.\( m=4 \)
D.\( m=2 \)
Na rysunku przedstawiono fragment wykresu funkcji \( f \), który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem \( y=\frac{1}{x} \) dla każdej liczby rzeczywistej \( x\ne 0 \).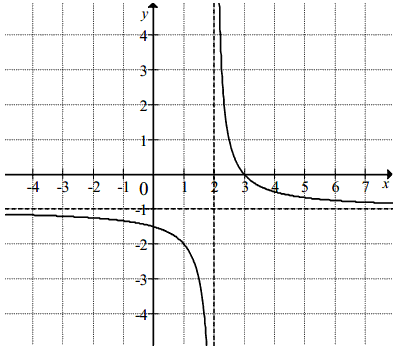 
a) Odczytaj z wykresu i zapisz zbiór tych wszystkich argumentów, dla których wartości funkcji \( f \) są większe od \( 0 \).
b) Podaj miejsce zerowe funkcji \( g \) określonej wzorem \( g(x)=f(x-3) \).
b) Podaj miejsce zerowe funkcji \( g \) określonej wzorem \( g(x)=f(x-3) \).
Funkcja \( f \) określona dla wszystkich liczb całkowitych dodatnich, przyporządkowuje liczbie \( x \) ostatnią cyfrę jej kwadratu. Zbiór wartości funkcji \( f \) zawiera dokładnie
A.\( 5 \) elementów
B.\( 6 \) elementów
C.\( 9 \) elementów
D.\( 10 \) elementów
Funkcja \(f\) przyporządkowuje każdej liczbie naturalnej większej od \(1\) jej największy dzielnik będący liczbą pierwszą. Spośród liczb: \(f(42\)), \(f(44)\), \(f(45)\), \(f(48)\) największa to
A.\( f(42) \)
B.\( f(44) \)
C.\( f(45) \)
D.\( f(48) \)
Funkcja \(f\) określona jest wzorem \(f(x)=\sqrt{x+2\sqrt{6}}\). Wartość funkcji \(f\) dla argumentu \(x=(\sqrt{3}-\sqrt{2})^2\) jest równa
A.\( \sqrt{2} \)
B.\( \sqrt{3} \)
C.\( \sqrt{5} \)
D.\( \sqrt{6} \)
Do wykresu funkcji \(f(x)=(m-1)x+m^2+1\) należy punkt \(P=(0,5)\). Parametr \(m\) może być równy
A.\( 0 \)
B.\( 1 \)
C.\( 2 \)
D.\( \sqrt{6} \)
Do wykresu funkcji \(f(x)=\frac{a}{x-3}\) należy punkt \(A=(1,2)\). Wobec tego:
A.\( a=-4 \)
B.\( a=-3 \)
C.\( a=-2 \)
D.\( a=-1 \)
Znajdź wszystkie argumenty \(x\) dla których funkcje \(f(x)=x-3\) oraz \(g(x)=-\frac{2}{x}\) przyjmują tę samą wartość.
Dana jest funkcja \(f\) określona wzorem \(f(x)=\begin{cases} x-2\quad \text{dla } x\le 0 \\ \Bigl ||x+3|-4 \Bigl |\quad \text{dla } x\gt 0 \end{cases} \). Równanie \(f(x)=1\) ma dokładnie
A.jedno rozwiązanie
B.dwa rozwiązania
C.cztery rozwiązania
D.pięć rozwiązań
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{2x-8}{x}\) dla każdej liczby rzeczywistej \(x \ne 0\). Wówczas wartość funkcji \(f(\sqrt{2})\) jest równa
A.\( 2-4\sqrt{2} \)
B.\( 1-2\sqrt{2} \)
C.\( 1+2\sqrt{2} \)
D.\( 2+4\sqrt{2} \)
Na rysunku przedstawiony jest wykres funkcji \(f\).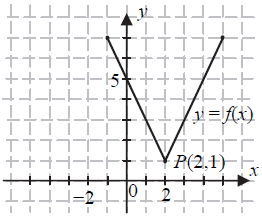 
Wskaż wzór funkcji, której wykres jest symetryczny do wykresu funkcji \(f\) względem osi \(Oy\) układu współrzędnych.
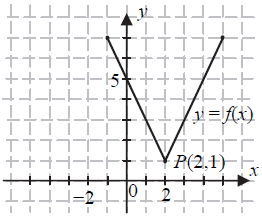Wskaż wzór funkcji, której wykres jest symetryczny do wykresu funkcji \(f\) względem osi \(Oy\) układu współrzędnych. A.\( y=f(x-4) \)
B.\( y=f(x)-4 \)
C.\( y=f(x+4) \)
D.\( y=f(x)+4 \)