Równanie okręgu

Drukuj

Poziom podstawowy

Twierdzenie

Okrąg o środku w punkcie \((a,b)\) i promieniu \(r\gt0\), jest zbiorem wszystkich punktów płaszczyzny \((x,y)\) spełniających równanie: \[(x-a)^2 + (y-b)^2 = r^2\] Powyższe równanie nazywamy równaniem okręgu w postaci kanonicznej.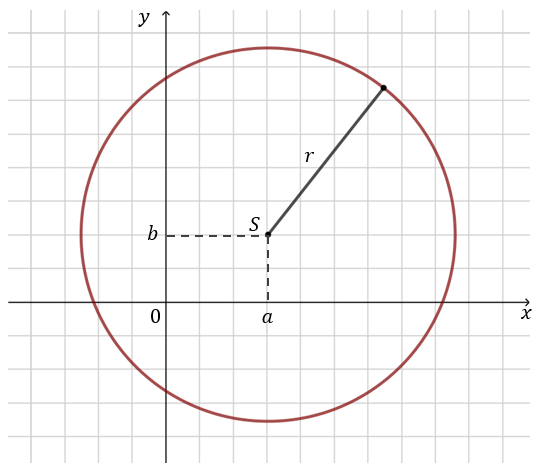

Szybka nawigacja do zadania numer: 5 10 15 20 25 30 .

Dany jest okrąg o równaniu \((x+3)^2+(y-4)^2=25\) . Środkiem \(S\) tego okręgu jest punkt:

A.\( S=(-3,-4) \)

B.\( S=(3,4) \)

C.\( S=(3,-4) \)

D.\( S=(-3,4) \)

Odległość między środkami okręgów o równaniach \((x+1)^2+(y-2)^2=9\) oraz \(x^2+y^2=10\) jest równa

A.\( \sqrt{5} \)

B.\( \sqrt{10}-3 \)

C.\( 3 \)

D.\( 5 \)

Okrąg o równaniu \((x+2)^2+(y-1)^2=13\) ma promień równy

A.\( \sqrt{13} \)

B.\( 13 \)

C.\( 8 \)

D.\( 2\sqrt{2} \)

Dane są punkty \(S=(2, 1)\), \(M=(6, 4)\). Równanie okręgu o środku \(S\) i przechodzącego przez punkt \(M\) ma postać

A.\( (x-2)^2+(y-1)^2=5 \)

B.\( (x-2)^2+(y-1)^2=25 \)

C.\( (x-6)^2+(y-4)^2=5 \)

D.\( (x-6)^2+(y-4)^2=25 \)

Równanie \((x+6)^2+y^2=4\) opisuje okrąg o środku w punkcie \(S\) i promieniu \(r\). Wówczas:

A.\( S=(-6,0),\ r=4 \)

B.\( S=(6,0),\ r=4 \)

C.\( S=(6,0),\ r=2 \)

D.\( S=(-6,0),\ r=2 \)

Okrąg o równaniu \((x+5)^2+(y-9)^2=4\) ma środek \(S\) i promień \(r\). Wówczas:

A.\( S=(5,-9), r=2 \)

B.\( S=(5,-9), r=4 \)

C.\( S=(-5,9), r=2 \)

D.\( S=(-5,9), r=4 \)

Dany jest okrąg o równaniu \((x+4)^2+(y-6)^2=100\) . Środek tego okręgu ma współrzędne

A.\( (-4,-6) \)

B.\( (4,6) \)

C.\( (4,-6) \)

D.\( (-4,6) \)

Punkt \(O\) jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać: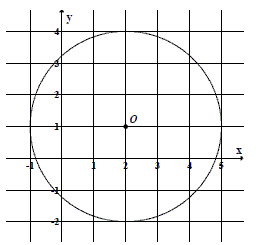

A.\( (x-2)^2+(y-1)^2=9 \)

B.\( (x-2)^2+(y-1)^2=3 \)

C.\( (x+2)^2+(y+1)^2=9 \)

D.\( (x+2)^2+(y+1)^2=3 \)

Wskaż równanie okręgu o promieniu \(6\).

A.\( x^2+y^2=3 \)

B.\( x^2+y^2=6 \)

C.\( x^2+y^2=12 \)

D.\( x^2+y^2=36 \)

Na okręgu o równaniu \( (x-2)^2+(y+7)^2=4 \) leży punkt

A.\(A=(-2,5) \)

B.\(B=(2,-5) \)

C.\(C=(2,-7) \)

D.\(D=(7,-2) \)

Wskaż równanie okręgu o środku \(S = (1,- 2)\) i promieniu \(r = 2\)

A.\( (x-1)^2+(y+2)^2=2 \)

B.\( (x+1)^2+(y-2)^2=2 \)

C.\( (x-1)^2+(y+2)^2=4 \)

D.\( (x+1)^2+(y-2)^2=4 \)

Liczba punktów wspólnych okręgu o równaniu \( (x+3)^2+(y-1)^2=4 \) z osiami układu współrzędnych jest równa

A.\(0 \)

B.\(1 \)

C.\(2 \)

D.\(4 \)

Środek \( S \) okręgu o równaniu \( x^2+y^2+4x-6y-221=0 \) ma współrzędne

A.\(S=(-2,3) \)

B.\(S=(2,-3) \)

C.\(S=(-4,6) \)

D.\(S=(4,-6) \)

Liczba punktów wspólnych okręgu o równaniu \((x-1)^2+y^2=4\) z prostą \(y=-1\) jest równa

A.\( 0 \)

B.\( 1 \)

C.\( 2 \)

D.\( 3 \)

Ile punktów wspólnych ma prosta o równaniu \(y=-x+2\) z okręgiem o środku w początku układu współrzędnych i promieniu \(2\)?

A.\( 0 \)

B.\( 1 \)

C.\( 2 \)

D.\( 3 \)

Ile punktów wspólnych ma prosta o równaniu \(y = 3\) z okręgiem o środku w punkcie \(S(1, 2)\) i promieniu \(1\)?

A.\( 0 \)

B.\( 1 \)

C.\( 2 \)

D.\( 3 \)

Ile punktów wspólnych ma prosta o równaniu \(y=2x+1\) z okręgiem o środku w punkcie \(S=(2, -2)\) i promieniu \(1\)?

A.\( 0 \)

B.\( 1 \)

C.\( 2 \)

D.\( 3 \)

Styczną do okręgu \((x - 1)^2 + y^2 - 4 = 0\) jest prosta równaniu

A.\( x=1 \)

B.\( x=3 \)

C.\( y=0 \)

D.\( y=4 \)

Wyznacz równanie okręgu o środku w punkcie \(S=(4, −2)\) i przechodzącego przez punkt \(O=(0, 0)\).

\((x-4)^2+(y+2)^2=20\)

Wyznacz równanie okręgu stycznego do osi \(Oy\), którego środkiem jest punkt \(S=(3, -5)\).

\((x-3)^2+(y+5)^2=9\)

Wyznacz równanie okręgu o środku w punkcie \(S = (3, -5)\) przechodzącego przez początek układu współrzędnych.

\((x-3)^2+(y+5)^3=34\)

Prosta o równaniu \(3x - 4y - 36 = 0\) przecina okrąg o środku \(S = (3, 12)\) w punktach \(A\) i \(B\). Długość odcinka \(AB\) jest równa \(40\). Wyznacz równanie tego okręgu.

\((x-3)^2+(y-12)^2=625\)

Prosta o równaniu \(y = x + 2\) przecina okrąg o równaniu \((x - 3)^2 + (y - 5)^2 = 25\) w punktach \(A\) i \(B\). Oblicz współrzędne punktów \(A\) i \(B\) oraz wyznacz równanie stycznej do danego okręgu przechodzącej przez jeden z tych punktów.

\(y=-x+8-5\sqrt{2}\)

Wyznacz równanie okręgu przechodzącego przez punkt \(A = (2, 1)\) i stycznego do obu osi układu współrzędnych. Rozważ wszystkie przypadki.

\((x-1)^2+(y-1)^2=1\) lub \((x-5)^2+(y-5)^2=25\)

Okrąg o środku w punkcie \(S=(3,7)\) jest styczny do prostej o równaniu \(y=2x-3\). Oblicz współrzędne punktu styczności.

\(\left(\frac{23}{5}; \frac{31}{5}\right)\)

Prosta \(y = x + 4\) przecina okrąg o równaniu \((x + 1)^2 + (y - 2)^2 = 25\) w punktach \(A\) i \(B\). Oblicz współrzędne punktów \(A\) i \(B\), a następnie oblicz obwód trójkąta \(ABS\), gdzie \(S\) jest środkiem danego okręgu.

\(A=(-5,1)\), \(B=(2,6)\), \(Ob=10+7\sqrt{2}\)

Długość okręgu opisanego równaniem \(x^2-4x+y^2-4=0\) jest równa:

A.\( 4\sqrt{2}\pi \)

B.\( 4\pi \)

C.\( 2\sqrt{2}\pi \)

D.\( 8\sqrt{2}\pi \)

Środkiem okręgu o równaniu \( (x+2)^2+(y-3)^2=16 \) jest punkt:

A.\(S=(2,3) \)

B.\(S=(-2,3) \)

C.\(S=(2,-3) \)

D.\(S=(-2,-3) \)

Liczba punktów wspólnych okręgu o równaniu \( (x+2)^2+(y-3)^2=4\ \) z osiami układu współrzędnych jest równa

A.\(0 \)

B.\(1 \)

C.\(2 \)

D.\(4 \)

Punkt \( P=(-1,0) \) leży na okręgu o promieniu \( 3 \). Równanie tego okręgu może mieć postać

A.\((x+1)^2+y^2=9 \)

B.\(x^2+\left ( y-\sqrt{2} \right )^2=3 \)

C.\((x+1)^2+(y+3)^2=9 \)

D.\((x+1)^2+y^2=3 \)

Okrąg przedstawiony na rysunku ma środek w punkcie \(O=(3,1)\) i przechodzi przez punkty \(S=(0,4)\) i \(T=(0,-2)\). Okrąg ten jest opisany przez równanie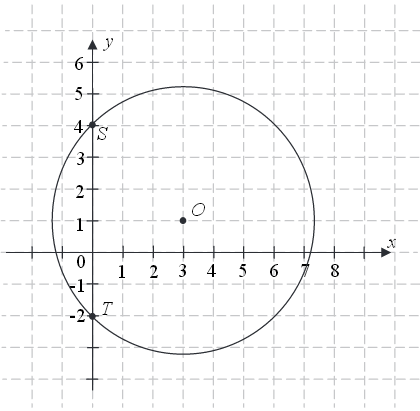

A.\( (x+3)^2+(y+1)^2=18 \)

B.\( (x-3)^2+(y+1)^2=18 \)

C.\( (x-3)^2+(y-1)^2=18 \)

D.\( (x+3)^2+(y-1)^2=18 \)

Okrąg opisany równaniem \((x−3)^2 + (y + 2)^2 = r^2\) jest styczny do osi \(Oy\). Promień \(r\) tego okręgu jest równy

A.\( \sqrt{13} \)

B.\( \sqrt{5} \)

C.\( 3 \)

D.\( 2 \)