Poziom rozszerzony - dodatkowe zadania
Poniżej zamieściłem playlistę z różnymi zadaniami z mojej strony, które wchodzą w zakres poziomu rozszerzonego.
W tym nagraniu wideo omawiam metodę rozwiązywania równań trygonometrycznych i pokazuję jak najlepiej rysować wykresy sinusa i cosinusa.
Czas lekcji: 25 min.
Rozwiąż nierówność \(|2x - 5| - |x + 4| \le 2 - 2x\).
Dana jest funkcja \( f \) określona wzorem \( f(x)=\frac{\vert{x+3}\vert+\vert{x-3}\vert}{x} \) dla każdej liczby rzeczywistej \( x\ne 0 \). Wyznacz zbiór wartości tej funkcji.
Rozwiąż nierówność \(x^4 + x^2 \ge 2x\).
Rozwiąż równanie \( \sqrt{3}\cdot \cos x=1+\sin x \) w przedziale \( \langle 0, 2\pi \rangle \) .
Rozwiąż równanie \(\sin x|\cos x|=0,25\), gdzie \(x\in \langle 0; 2\pi \rangle\).
Rozwiąż równanie \(\cos 2x + \cos x + 1 = 0\) dla \(x\in \langle 0,2\pi \rangle\).
Rozwiąż równanie \(\cos2x + 2 = 3\cos x\).
Wyznacz wszystkie wartości parametru \(m\), dla których równanie \(x^2 + 2(1 - m)x + m^2 - m = 0\) ma dwa różne rozwiązania rzeczywiste \(x_1\), \(x_2\) spełniające warunek \(x_1 \cdot x_2 \le 6m \le x_1^2 + x_2^2\) .
Oblicz wszystkie wartości parametru \(m\), dla których równanie \(x^2 - (m + 2)x + m + 4 = 0\) ma dwa różne pierwiastki rzeczywiste \(x_1\), \(x_2\) takie, że \({x_1}^4 + {x_2}^4 = 4m^3 + 6m^2 - 32m + 12\).
Wyznacz wszystkie wartości parametru \( m \), dla których funkcja kwadratowa \( f(x)=x^2-(2m+2)x+2m+5 \) ma dwa różne pierwiastki \( \ x_1, x_2 \) takie, że suma kwadratów odległości punktów \( A=(x_1, 0)\ \text{i}\ B=(x_2, 0) \) od prostej o równaniu \( x+y+1=0 \) jest równa \( 6 \).
Wyznacz wszystkie całkowite wartości parametru \( m \), dla których równanie \[ \left (x^3+2x^2+2x+1 \right) \left [ x^2-(2m+1)x+m^2+m \right]=0 \] ma trzy, parami różne, pierwiastki rzeczywiste, takie że jeden z nich jest średnią arytmetyczną dwóch pozostałych.
Reszta z dzielenia wielomianu \(W(x) = 4x^3 - 5x^2 - 23x + m\) przez dwumian \(x + 1\) jest równa \(20\). Oblicz wartość współczynnika \(m\) oraz pierwiastki tego wielomianu.
Wykaż, że dla dowolnej wartości parametru \(m\) równanie: \(-x^2+(2m^2+3)x-m^4-1=0\) ma dwa różne pierwiastki dodatnie.
Ciąg liczbowy \((a, b, c)\) jest arytmetyczny i \(a + b + c = 33\), natomiast ciąg \((a - 1, b + 5, c + 19)\) jest geometryczny. Oblicz \(a, b, c\).
Trzy liczby tworzą ciąg geometryczny. Jeżeli do drugiej liczby dodamy \(8\), to ciąg ten zmieni się w arytmetyczny. Jeżeli zaś do ostatniej liczby nowego ciągu arytmetycznego dodamy \(64\), to tak otrzymany ciąg będzie znów geometryczny. Znajdź te liczby. Uwzględnij wszystkie możliwości.
Liczby \(a, b, c\) tworzą w podanej kolejności ciąg geometryczny. Suma tych liczb jest równa \(93\). Te same liczby, w podanej kolejności są pierwszym, drugim i siódmym wyrazem ciągu arytmetycznego. Oblicz \(a, b\) i \(c\).
Wyznacz wzór na \(n\)-ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa \(10\), a wyrazy trzeci, piąty i trzynasty tworzą w podanej kolejności ciąg geometryczny.
Trójkąt \( ABC\ \) jest wpisany w okrąg o środku \( S \). Kąty wewnętrzne \( CAB, ABC \) i \( BCA \) tego trójkąta są równe, odpowiednio, \( \alpha , 2\alpha \) i \( 4\alpha \). Wykaż, że trójkąt \( ABC \) jest rozwartokątny, i udowodnij, że miary wypukłych kątów środkowych \( ASB, ASC \) i \( BSC\ \) tworzą w podanej kolejności ciąg arytmetyczny.
Ciąg geometryczny \( (a_n) \) ma \( 100 \) wyrazów i są one liczbami dodatnimi. Suma wszystkich wyrazów o numerach nieparzystych jest sto razy większa od sumy wszystkich wyrazów o numerach parzystych oraz \( \log a_1+\log a_2+\log a_3+...+\log a_{100}=100 \). Oblicz \( a_1 \).
Wiedząc, że ciąg \((a_n)\) jest ciągiem arytmetycznym oraz wyraz ogólny ciągu \((b_n)\) określony jest wzorem \(b_n = 5^{a_n}\), wykaż, że ciąg \((b_n)\) jest ciągiem geometrycznym. Wyznacz, w zależności od \(n\), iloczyn \(b_1\cdot b_2\cdot b_3\cdot ...\cdot b_n\), przyjmując, że pierwszy wyraz ciągu \((a_n)\) jest równy \(1\), a jego różnica jest równa \(3\).
Rzucamy cztery razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb oczek otrzymanych we wszystkich czterech rzutach będzie równy \(60\).
Oblicz, ile jest liczb naturalnych sześciocyfrowych, w zapisie których występuje dokładnie trzy razy cyfra \(0\) i dokładnie raz występuje cyfra \(5\).
Prosta o równaniu \(3x - 4y - 36 = 0\) przecina okrąg o środku \(S = (3, 12)\) w punktach \(A\) i \(B\). Długość odcinka \(AB\) jest równa \(40\). Wyznacz równanie tego okręgu.
W układzie współrzędnych rozważmy wszystkie punkty \(P\) postaci: \(P = \left (\frac{1}{2}m + \frac{5}{2}, m \right )\) gdzie \(m\in \langle -1,7 \rangle\). Oblicz najmniejszą i największą wartość \(|PQ|^2\), gdzie \(Q = \left (\frac{55}{2}, 0 \right )\).
Dany jest trójkąt \(ABC\), w którym \(|AC| = 17\) i \(|BC| = 10\). Na boku \(AB\) leży punkt \(D\) taki, że \(|AD|:|DB|=3:4\) oraz \(|DC| = 10\). Oblicz pole trójkąta \(ABC\).
Dany jest trójkąt prostokątny \(ABC\), w którym \(|BC| = 30\), \(|AC| = 40\), \(|AB| = 50\). Punkt \(W\) jest środkiem okręgu wpisanego w ten trójkąt. Okrąg wpisany w trójkąt \(ABC\) jest styczny do boku \(AB\) w punkcie \(M\). Oblicz długość odcinka \(CM\). 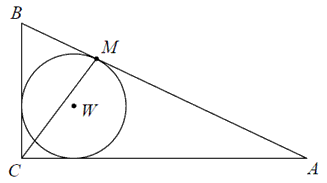

Na zewnątrz trójkąta prostokątnego \(ABC\), w którym \(|\sphericalangle ACB| = 90\) oraz \(|AC| = 5\), \(|BC| = 12\) zbudowano kwadrat \(ACDE\) (patrz rysunek). Punkt \(H\) leży na prostej \(AB\) i kąt \(|\sphericalangle EHA| = 90^\circ\). Oblicz pole trójkąta \(HAE\). 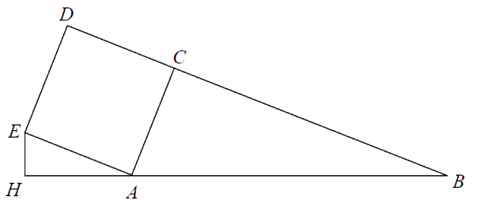

Na rysunku przedstawiony jest fragment wykresu funkcji logarytmicznej \(f\) określonej wzorem \(f(x)=\log_2 (x-p)\). 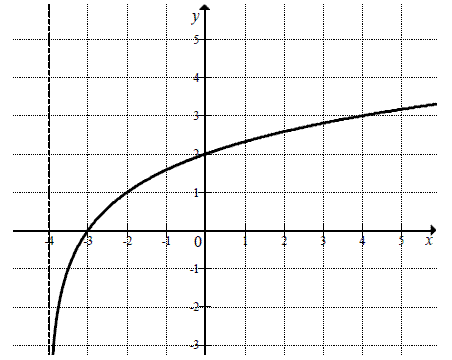 a) Podaj wartość \(p\).
a) Podaj wartość \(p\).
b) Narysuj wykres funkcji określonej wzorem \(y = |f(x)|\).
c) Podaj wszystkie wartości parametru \(m\), dla których równanie \(|f(x)| = m\) ma dwa rozwiązania o przeciwnych znakach.
 a) Podaj wartość \(p\).
a) Podaj wartość \(p\).b) Narysuj wykres funkcji określonej wzorem \(y = |f(x)|\).
c) Podaj wszystkie wartości parametru \(m\), dla których równanie \(|f(x)| = m\) ma dwa rozwiązania o przeciwnych znakach.
W ostrosłupie \(ABCS\) podstawa \(ABC\) jest trójkątem równobocznym o boku długości \(a\). Krawędź \(AS\) jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka \(A\) od ściany \(BCS\) jest równa \(d\). Wyznacz objętość tego ostrosłupa.
Wyznacz cztery kolejne liczby całkowite takie, że największa z nich jest równa sumie kwadratów trzech pozostałych liczb.
Udowodnij, że jeżeli \(a + b \ge 0\), to prawdziwa jest nierówność \(a^3 + b^3 \ge a^2b + ab^2\).
Wykaż, że prawdziwa jest nierówność \(\sqrt{2^{50} + 1} + \sqrt{2^{50} - 1} \lt 2^{26}\).
Trapez równoramienny \(ABCD\) o podstawach \(AB\) i \(CD\) jest opisany na okręgu o promieniu \(r\). Wykaż, że \(4r^2 = |AB| \cdot |CD|\).
Udowodnij, że jeśli:
a) \(x, y\) są liczbami rzeczywistymi, to \(x^2 + y^2 \ge 2xy\).
b) \(x, y, z\) są liczbami rzeczywistymi takimi, że \(x + y + z = 1\), to \(x^2 + y^2 + z^2 \ge 1/3\).
b) \(x, y, z\) są liczbami rzeczywistymi takimi, że \(x + y + z = 1\), to \(x^2 + y^2 + z^2 \ge 1/3\).
Udowodnij, że dla każdych dwóch liczb rzeczywistych dodatnich \( x, y \) prawdziwa jest nierówność \((x+1)\frac{x}{y}+(y+1)\frac{y}{x}>2 \).
Dane są trzy okręgi o środkach \( A, B, C \) i promieniach równych odpowiednio \( r, 2r, 3r \). Każde dwa z tych okręgów są zewnętrznie styczne: pierwszy z drugim w punkcie \( K \), drugi z trzecim w punkcie \( L \) i trzeci z pierwszym w punkcie \( M \). Oblicz stosunek pola trójkąta \( KLM \) do pola trójkąta \( ABC \).
Punkty \( A, B, C, D, E, F \) są kolejnymi wierzchołkami sześciokąta foremnego, przy czym \( A=(0, 2\sqrt{3}),B=(2,0) \), a \( C \) leży na osi \( \ Ox \). Wyznacz równanie stycznej do okręgu opisanego na tym sześciokącie przechodzącej przez wierzchołek \(E \).
Oblicz objętość ostrosłupa trójkątnego \( ABCS \), którego siatkę przedstawiono na rysunku. 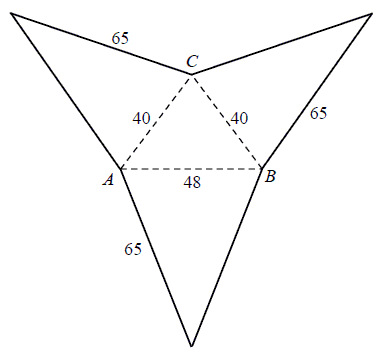

Z urny zawierającej \(10\) kul ponumerowanych kolejnymi liczbami od \(1\) do \(10\) losujemy jednocześnie trzy kule. Oblicz prawdopodobieństwo zdarzenia \( A \) polegającego na tym, że numer jednej z wylosowanych kul jest równy sumie numerów dwóch pozostałych kul.
Narysuj wykres funkcji: \[ f(x)=\begin{cases} -2^{x+1}+2,\quad \text{dla } x\le 0\\ -|x-4|+4,\quad \text{dla } x> 0 \end{cases} \] Określ liczbę rozwiązań równania \(|f(x)|=m\) w zależności od parametru \(m\).
O wielomianie \(W(x)=2x^3+ax^2+bx+c\) wiadomo, że liczba \(1\) jest jego pierwiastkiem dwukrotnym oraz że \(W(x)\) jest podzielny przez dwumian \(x + 2\). Oblicz współczynniki \(a, b, c\). Dla obliczonych wartości \(a, b, c\) rozwiąż nierówność \(W(x+1)\lt 0\).
Liczby \(a\), \(b\), \(k\) są całkowite i \(k\) jest różna od zera. Wykaż, że jeśli liczby \(a+b\) oraz \(a\cdot b\) są podzielne przez \(k\), to liczba \(a^3-b^3\) też jest podzielna przez \(k\).
Określ dziedzinę funkcji: \(f(x)=\sqrt{\text{log}_{2}(\text{log}_{\frac{1}{3}}(x+1))}\).
Okrąg o środku \(A\) i promieniu długości \(r\) jest styczny zewnętrznie do okręgu o środku \(B\) i promieniu długości \(R\) (\(R> r\)). Prosta \(k\) jest styczna jednocześnie do obu okręgów i tworzy z prostą \(AB\) kąt ostry \(\alpha \). Wyznacz \(\sin \alpha \) w zależności od \(r\) i \(R\).
W trójkącie \(ABC\) punkty \(K = (2, 2), L = (-2, 1)\) i \(M = (-1,-1)\) są odpowiednio środkami boków \(AB, BC, AC\). Wyznacz współrzędne wierzchołków trójkąta \(A' B' C'\), który jest obrazem trójkąta \(ABC\) w symetrii środkowej względem początku układu współrzędnych.
W trójkącie \(ABC\) kąt przy wierzchołku \(B\) jest ostry, długość promienia okręgu opisanego na tym trójkącie jest równa \(5\) oraz \(|AC|=6, |AB|=10\). Na boku \(BC\) wybrano taki punkt \(K\), że \(|BK|=2\). Oblicz długość odcinka \(AK\).
W zielonym pudełku jest 10 monet pięciozłotowych i 5 monet dwuzłotowych, a w białym pudełku są 2 monety pięciozłotowe i 3 monety dwuzłotowe. Z zielonego pudełka losujemy jedną monetę i wrzucamy ją do białego pudełka. Następnie z białego pudełka losujemy jednocześnie 2 monety. Oblicz prawdopodobieństwo, że z białego pudełka wylosujemy w sumie 7 złotych.
W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość \(a\). Ostrosłup ten przecięto płaszczyzną przechodzącą przez środki dwóch sąsiednich krawędzi podstawy i wierzchołek ostrosłupa. Płaszczyzna tego przekroju tworzy z płaszczyzną podstawy kąt o mierze \(\alpha\). Oblicz objętość tego ostrosłupa.
Oblicz \(\left(\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\right)^2\).
Miary dwóch kątów trójkąta wynoszą \(\frac{\pi }{6}\) i \(\frac{\pi }{5}\). Oblicz miarę trzeciego kąta. Odpowiedź podaj w stopniach.
Dane jest równanie \(\sin x = a^2 + 1\), z niewiadomą \(x\). Wyznacz wszystkie wartości parametru \(a\), dla których dane równanie nie ma rozwiązań.
Funkcja f jest określona wzorem \(f(x)=\begin{cases} x+5 &\text{ dla } x\lt -5 \\ -x+2 &\text{ dla } -5\le x\lt 5 \\ x-6 &\text{ dla } x\ge 5 \end{cases} \). Wyznacz miejsca zerowe tej funkcji.
W kolejce do kasy biletowej ustawiły się cztery dziewczynki, a za nimi pięciu chłopców. Oblicz liczbę wszystkich możliwych ustawień osób w tej kolejce.
Rozwiąż równanie \(\log_5(\log_4(\log_2x))=0\).
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{1}{x+1}-1\) dla wszystkich liczb rzeczywistych \(x\ne -1\). Rozwiąż nierówność \(f(x)\gt f(2-x)\).
Narysuj wykres funkcji f określonej w przedziale 〈-2, 2〉 wzorem:
a) f(x) = 2x - 1 b) f(x) = 2x - 1.
a) f(x) = 2x - 1 b) f(x) = 2x - 1.
Pole wycinka koła o promieniu 3 cm jest równe 2 cm2. Oblicz miarę łukową kąta środkowego tego wycinka.
Punkty A = (1, 1), B = (5, 5), C = (3, 5) są wierzchołkami trapezu równoramiennego ABCD niebędącego równoległobokiem, w którym AB || CD.
a) Wyznacz równanie osi symetrii tego trapezu.
b) Oblicz pole tego trapezu.
a) Wyznacz równanie osi symetrii tego trapezu.
b) Oblicz pole tego trapezu.
Na okręgu zaznaczono sześć różnych punktów. Ile różnych wielokątów wypukłych o wszystkich wierzchołkach w tych punktach można narysować?
Dla jakich wartości parametru \(m\) reszta z dzielenia wielomianu \(x^{17}-m x^{15}+(m-2) x^{10}+2 x+m^2-2\) przez dwumian \(x-1\) jest równa 3?
Wyznacz równanie okręgu o środku A = (2, 3), stycznego do prostej o równaniu x - 2y + 1 = 0.
Niech \(A\) będzie zbiorem wszystkich liczb \(x\), które spełniają równość \(|x - 1| + |x - 3| = 2\). Niech \(B\) będzie zbiorem wszystkich punktów na osi liczbowej, których suma odległości od punktów \(4\) i \(6\) jest niewiększa niż \(4\). Zaznacz na osi liczbowej zbiory \(A\) i \(B\) oraz wszystkie punkty, które należą jednocześnie do \(A\) i do \(B\).
Przedział \(\left (-\frac{3}{2}, 0 \right )\) jest zbiorem wszystkich rozwiązań nierówności \(\frac{2}{x} \lt m\) z niewiadomą \(x\). Oblicz \(m\).
Rozpatrujemy wszystkie prostokąty o polu równym 6, których dwa sąsiednie boki zawarte są w osiach Ox i Oy układu współrzędnych. Wyznacz równanie krzywej będącej zbiorem tych wierzchołków rozpatrywanych prostokątów, które nie leżą na żadnej z osi układu współrzędnych. Narysuj tę krzywą.