Postać ogólna, kanoniczna i iloczynowa funkcji kwadratowej
Wzór funkcji kwadratowej można często zapisać na wiele różnych sposobów. Najważniejsze z nich to postać ogólna, postać kanoniczna i postać iloczynowa.
Funkcja kwadratowa dana wzorem ogólnym: \[f(x)=x^2+5x+6\] może być zapisana w innej postaci:
- \(f(x)=(x+2)(x+3)\) - postać iloczynowa
- \(f(x)=\left ( x+\frac{5}{2} \right )^2-\frac{1}{4}\) - postać kanoniczna
- \(f(x)=x(x+5)+6\)
- \(f(x)=x^2+5(x+1)+1\)
Definicja
Postać ogólna funkcji kwadratowej to: \[ f(x)=ax^2+bx+c \] gdzie \(a, b, c\) są współczynnikami liczbowymi i \(a \ne 0\).- Czy ramiona paraboli są skierowane do góry (\(a > 0\)), czy do dołu (\(a < 0\)).
- Punkt przecięcia paraboli z osią \(y\)-ów, który ma współrzędne \((0, c)\).
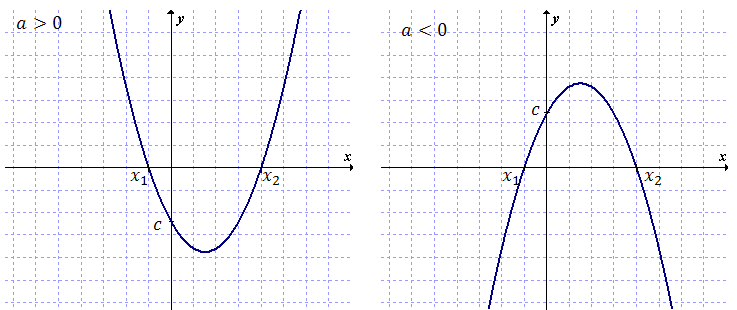 Na powyższych wykresach zaznaczono również miejsca zerowe obu funkcji kwadratowych (oznaczone symbolami \(x_1\) oraz \(x_2\)). Mając wzór ogólnym funkcji kwadratowej możemy łatwo obliczyć miejsca zerowe \(x_1\) i \(x_2\). Wystarczy najpierw obliczyć deltę, korzystając ze wzoru: \[ \Delta =b^2-4ac \] Jeżeli delta wyszła większa od zera, to miejsca zerowe istnieją i możemy je obliczyć korzystając ze wzorów: \[ \begin{split} {x}_{1}&=\frac{-b-\sqrt{\Delta }}{2a}\\[6pt] {x}_{2}&=\frac{-b+\sqrt{\Delta }}{2a} \end{split} \] Chcąc policzyć współrzędne wierzchołka W funkcji kwadratowej danej w postaci ogólnej, skorzystamy ze wzorów: \[ W=\left ( \frac{-b}{2a}, \frac{-\Delta }{4a} \right ) \]
Na powyższych wykresach zaznaczono również miejsca zerowe obu funkcji kwadratowych (oznaczone symbolami \(x_1\) oraz \(x_2\)). Mając wzór ogólnym funkcji kwadratowej możemy łatwo obliczyć miejsca zerowe \(x_1\) i \(x_2\). Wystarczy najpierw obliczyć deltę, korzystając ze wzoru: \[ \Delta =b^2-4ac \] Jeżeli delta wyszła większa od zera, to miejsca zerowe istnieją i możemy je obliczyć korzystając ze wzorów: \[ \begin{split} {x}_{1}&=\frac{-b-\sqrt{\Delta }}{2a}\\[6pt] {x}_{2}&=\frac{-b+\sqrt{\Delta }}{2a} \end{split} \] Chcąc policzyć współrzędne wierzchołka W funkcji kwadratowej danej w postaci ogólnej, skorzystamy ze wzorów: \[ W=\left ( \frac{-b}{2a}, \frac{-\Delta }{4a} \right ) \]W tym nagraniu wideo omawiam postać ogólną, kanoniczną i iloczynową funkcji kwadratowej.