Objętość bryły ograniczonej powierzchniami
Poziom studiów
Oblicz objętość bryły ograniczonej ograniczonej paraboloidą \(z = x^2 + y^2\), płaszczyzną \(z = 0\) i walcem \(x^2+y^2=r^2\).
Jeżeli płaszczyznę \(z = 0\) ograniczymy walcem \(x^2+y^2=r^2\), to otrzymamy koło o równaniu: \(x^2+y^2\le r^2\): Zatem obszar ograniczony danymi płaszczyznami, możemy zapisać tak: \[V=\{(x,y,z)\in \mathbb{R}^3: z\ge0,\ z\le x^2+y^2,\ x^2+y^2\le r^2 \}\]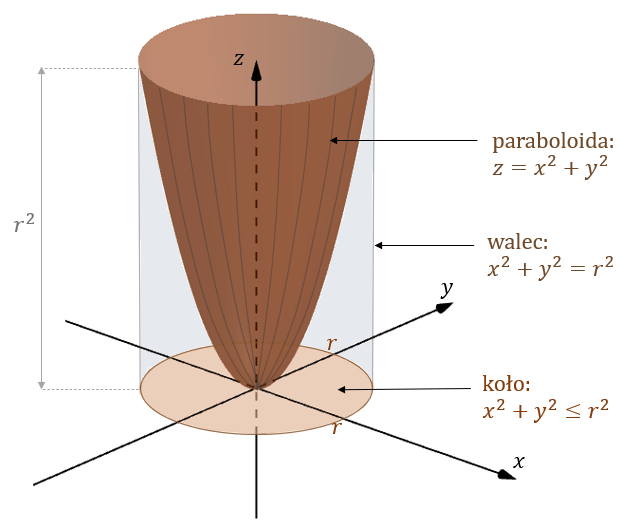 
Aby wyznaczyć objętość szukanej bryły, należy scałkować obszar \(V\) po wszystkich trzech zmiennych: \[\iiint\limits_V dx\,dy\,dz\] Możemy łatwo przejść na całkę podwójną, wprowadzamy obszar całkowania na płaszczyźnie \(XY\): \[D=\{(x,y)\in \mathbb{R}^2: x^2+y^2\le r^2\}\] (obszar \(D\), to oczywiście nasze koło, powstałe z ograniczenia płaszczyzny \(z=0\) walcem \(x^2+y^2=r^2\)).
Teraz możemy zapisać: \[ \begin{split} &\iiint\limits_V dx\,dy\,dz=\\[6pt] =&\iint\limits_D \left(\int\limits_{0}^{x^2+y^2}dz \right) dx\,dy=\\[6pt] =&\iint\limits_D \left(z \vert_0^{x^2+y^2}\right) dx\,dy=\\[6pt] =&\iint\limits_D (x^2+y^2 - 0)\ dx\,dy=\\[6pt] =&\iint\limits_D (x^2+y^2)\ dx\,dy \end{split} \]
Aby wyznaczyć objętość szukanej bryły, należy scałkować obszar \(V\) po wszystkich trzech zmiennych: \[\iiint\limits_V dx\,dy\,dz\] Możemy łatwo przejść na całkę podwójną, wprowadzamy obszar całkowania na płaszczyźnie \(XY\): \[D=\{(x,y)\in \mathbb{R}^2: x^2+y^2\le r^2\}\] (obszar \(D\), to oczywiście nasze koło, powstałe z ograniczenia płaszczyzny \(z=0\) walcem \(x^2+y^2=r^2\)).Teraz możemy zapisać: \[ \begin{split} &\iiint\limits_V dx\,dy\,dz=\\[6pt] =&\iint\limits_D \left(\int\limits_{0}^{x^2+y^2}dz \right) dx\,dy=\\[6pt] =&\iint\limits_D \left(z \vert_0^{x^2+y^2}\right) dx\,dy=\\[6pt] =&\iint\limits_D (x^2+y^2 - 0)\ dx\,dy=\\[6pt] =&\iint\limits_D (x^2+y^2)\ dx\,dy \end{split} \]
Powyższe rachunki zapisałem po to, aby dokładnie pokazać skąd wzięła się całka \(\iint\limits_D (x^2+y^2)\ dx\,dy\). Przy odrobinie wprawy można byłoby zacząć rozwiązanie zadania od razu od zapisania tej całki.
W celu policzenia tej całki warto wykonać zamianę zmiennych na współrzędne biegunowe: \[\begin{cases} x=R\cos \varphi \\ y=R\sin \varphi \end{cases} \] gdzie \(R\in \langle0,r \rangle\) oraz \(\varphi\in \langle 0,2\pi \rangle\). Jakobian (wyznacznik macierzy, zbudowanej z pierwszych pochodnych cząstkowych), tego podstawienia to: \[J=\begin{vmatrix} \cos\varphi & -R\sin\varphi \\ \sin\varphi & R\cos\varphi \end{vmatrix}=R \] Możemy teraz zdefiniować nowy obszar całkowania dla współrzędnych biegunowych: \[\Delta=\{(R,\varphi)\in \mathbb{R}^2: 0\le R\le r,\ 0\le \varphi\le 2\pi \}\] i dalej na nim liczyć całkę: \[ \begin{split} &\iint\limits_D (x^2+y^2)dx\,dy=\\[6pt] =&\iint\limits_\Delta (R^2\cos^2\varphi +R^2\sin^2\varphi)\cdot RdR\,d\varphi =\\[6pt] =&\iint\limits_\Delta (R^2(\cos^2\varphi +\sin^2\varphi))\cdot RdR\,d\varphi =\\[6pt] =&\iint\limits_\Delta (R^2)\cdot RdR\,d\varphi =\\[6pt] =&\iint\limits_\Delta R^3 dR\,d\varphi =\\[6pt] =&\int\limits_{0}^{2\pi}\left(\int\limits_{0}^{2}R^3 dR \right)d\varphi= \\[6pt] =&\int\limits_{0}^{2\pi}\left.\left( \frac{R^4}{4}\right)\right\vert_0^r d\varphi= \\[6pt] =&\int\limits_{0}^{2\pi} \frac{r^4}{4} d\varphi= \\[6pt] =&\left.\frac{r^4}{4}\varphi\right\vert_0^{2\pi}= \frac{r^4}{4}\cdot 2\pi-0 = \frac{\pi r^4}{2} \end{split} \] Zatem szukana objętość bryły wynosi \(\frac{\pi r^4}{2}\). Zauważmy, że objętość wyliczona w powyższym przykładzie jest równa dokładnie połowie objętości walca ograniczającego naszą bryłę. Walec ma wysokość \(r^2\), zatem jego objętość to: \[\pi r^2 \cdot r^2=\pi r^4\]
Można łatwo sprawdzić, że dla paraboloidy danej wzorem: \(z = a(x^2 + y^2)\), gdzie \(a\in \mathbb{R}\backslash \{0\} \) sytuacja będzie analogiczna - objętość bryły pod paraboloidą będzie równa połowie objętości walca opisanego na tej paraboloidzie.
Oblicz objętość bryły ograniczonej płaszczyznami: \(z=0\), \(z=x^2+y^2+2\) oraz \(x^2+y^2=4\).
Płaszczyzny ograniczają obszar całkowania, który możemy zapisać tak: \[V=\{(x,y,z)\in \mathbb{R}^3: z\ge0,\ z\le x^2+y^2+2,\ x^2+y^2\le 4 \}\] Czyli mamy do obliczenia objętość między paraboloidą: \(z=x^2+y^2+2\), a kołem: \(x^2+y^2\le 4\):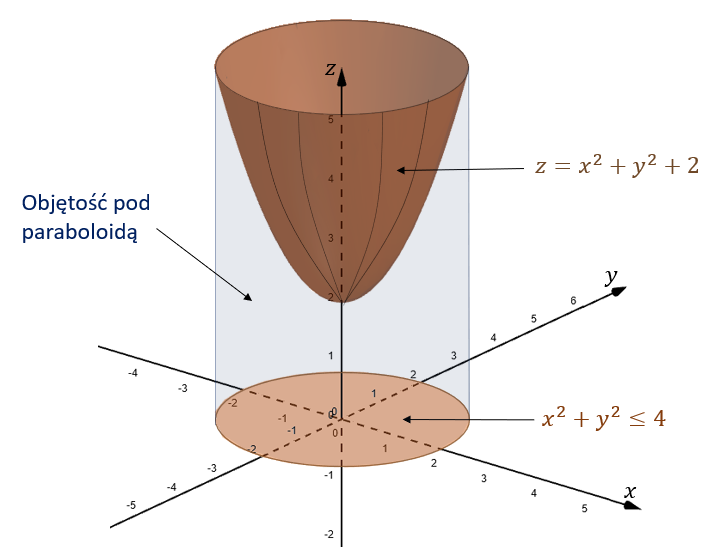 
Objętość liczymy jako całkę potrójną po wszystkich trzech zmiennych: \[\iiint\limits_V dx\,dy\,dz\] Żeby przejść na całkę podwójną, wprowadzamy obszar całkowania na płaszczyźnie \(XY\): \[D=\{(x,y)\in \mathbb{R}^2: x^2+y^2\le 4\}\] Teraz możemy zapisać: \[ \begin{split} &\iiint\limits_V dx\,dy\,dz=\\[6pt] =&\iint\limits_D \left(\int\limits_{0}^{x^2+y^2+2}dz \right) dx\,dy=\\[6pt] =&\iint\limits_D (x^2+y^2+2)dx\,dy \end{split} \] Obszar \(D\) jest kołem o promieniu \(2\), zatem możemy wykonać podstawienie na współrzędne biegunowe: \[\begin{cases} x=r\cos \varphi \\ y=r\sin \varphi \end{cases} \] gdzie \(r\in \langle0,2 \rangle\) oraz \(\varphi\in \langle 0,2\pi \rangle\). Jakobian tego przekształcenia to: \[J=\begin{vmatrix} \cos\varphi & -r\sin\varphi \\ \sin\varphi & r\cos\varphi \end{vmatrix}=r \] Możemy teraz zdefiniować nowy obszar całkowania: \[\Delta=\{(r,\varphi)\in \mathbb{R}^2: 0\le r\le 2,\ 0\le \varphi\le 2\pi \}\] i dalej na nim liczyć całkę: \[ \begin{split} &\iint\limits_D (x^2+y^2+2)dx\,dy=\\[6pt] =&\iint\limits_\Delta (r^2\cos^2\varphi +r^2\sin^2\varphi+2)\cdot rdr\,d\varphi =\\[6pt] =&\iint\limits_\Delta (r^2(\cos^2\varphi +\sin^2\varphi)+2)\cdot rdr\,d\varphi =\\[6pt] =&\iint\limits_\Delta (r^2+2)\cdot rdr\,d\varphi =\\[6pt] =&\iint\limits_\Delta (r^3+2r)dr\,d\varphi =\\[6pt] =&\int\limits_{0}^{2\pi}\left(\int\limits_{0}^{2}(r^3+2r)dr \right)d\varphi= \\[6pt] =&\int\limits_{0}^{2\pi}\left.\left( \frac{r^4}{4}+r^2 \right)\right\vert_0^2 d\varphi= \\[6pt] =&\int\limits_{0}^{2\pi} (4+4-0-0) d\varphi= \\[6pt] =&\int\limits_{0}^{2\pi} 8 d\varphi= \left.8\varphi\right\vert_0^{2\pi}= 8\cdot 2\pi-0 = 16\pi \end{split} \] Zatem szukana objętość bryły wynosi \(16\pi\).
Objętość liczymy jako całkę potrójną po wszystkich trzech zmiennych: \[\iiint\limits_V dx\,dy\,dz\] Żeby przejść na całkę podwójną, wprowadzamy obszar całkowania na płaszczyźnie \(XY\): \[D=\{(x,y)\in \mathbb{R}^2: x^2+y^2\le 4\}\] Teraz możemy zapisać: \[ \begin{split} &\iiint\limits_V dx\,dy\,dz=\\[6pt] =&\iint\limits_D \left(\int\limits_{0}^{x^2+y^2+2}dz \right) dx\,dy=\\[6pt] =&\iint\limits_D (x^2+y^2+2)dx\,dy \end{split} \] Obszar \(D\) jest kołem o promieniu \(2\), zatem możemy wykonać podstawienie na współrzędne biegunowe: \[\begin{cases} x=r\cos \varphi \\ y=r\sin \varphi \end{cases} \] gdzie \(r\in \langle0,2 \rangle\) oraz \(\varphi\in \langle 0,2\pi \rangle\). Jakobian tego przekształcenia to: \[J=\begin{vmatrix} \cos\varphi & -r\sin\varphi \\ \sin\varphi & r\cos\varphi \end{vmatrix}=r \] Możemy teraz zdefiniować nowy obszar całkowania: \[\Delta=\{(r,\varphi)\in \mathbb{R}^2: 0\le r\le 2,\ 0\le \varphi\le 2\pi \}\] i dalej na nim liczyć całkę: \[ \begin{split} &\iint\limits_D (x^2+y^2+2)dx\,dy=\\[6pt] =&\iint\limits_\Delta (r^2\cos^2\varphi +r^2\sin^2\varphi+2)\cdot rdr\,d\varphi =\\[6pt] =&\iint\limits_\Delta (r^2(\cos^2\varphi +\sin^2\varphi)+2)\cdot rdr\,d\varphi =\\[6pt] =&\iint\limits_\Delta (r^2+2)\cdot rdr\,d\varphi =\\[6pt] =&\iint\limits_\Delta (r^3+2r)dr\,d\varphi =\\[6pt] =&\int\limits_{0}^{2\pi}\left(\int\limits_{0}^{2}(r^3+2r)dr \right)d\varphi= \\[6pt] =&\int\limits_{0}^{2\pi}\left.\left( \frac{r^4}{4}+r^2 \right)\right\vert_0^2 d\varphi= \\[6pt] =&\int\limits_{0}^{2\pi} (4+4-0-0) d\varphi= \\[6pt] =&\int\limits_{0}^{2\pi} 8 d\varphi= \left.8\varphi\right\vert_0^{2\pi}= 8\cdot 2\pi-0 = 16\pi \end{split} \] Zatem szukana objętość bryły wynosi \(16\pi\). Oblicz objętość bryły ograniczonej płaszczyznami: \(z=4-x^2-y^2\) oraz \(2z=2+x^2+y^2\).
Płaszczyzny ograniczają obszar całkowania, który możemy zapisać tak: \[V=\{(x,y,z)\in \mathbb{R}^3: z=4-(x^2+y^2), z=1+\frac{1}{2}(x^2+y^2) \}\] Wyznaczmy część wspólną obu płaszczyzn: \[\begin{split} 4-(x^2+y^2)&=1+\frac{1}{2}(x^2+y^2)\\[6pt] \frac{3}{2}(x^2+y^2)&=3\\[6pt] x^2+y^2&=2 \end{split}\] Otrzymaliśmy równanie okręgu o promieniu \(\sqrt{2}\). Czyli mamy do obliczenia objętość bryły między dwiema paraboloidami, których przecięciem jest okrąg o równaniu \(x^2+y^2=2\). Korzystając z tego równania można dodatkowo wyliczyć dla jakiego parametru \(z\) powierzchnie przecinają się: \[z=4-(x^2+y^2)=4-2=2\] Możemy jeszcze łatwo wyznaczyć ekstrema obu paraboloid. Powierzchnia \(z=4-(x^2+y^2)\) największą wartość przyjmuje w punkcie \((0,0,4)\), a paraboloida \(z=1+\frac{1}{2}(x^2+y^2)\) przyjmuje wartość najmniejszą w punkcie \((0,0,1)\). Te informacje nie są potrzebne do rozwiązania zadania, ale ułatwią narysowanie dokładnego rysunku: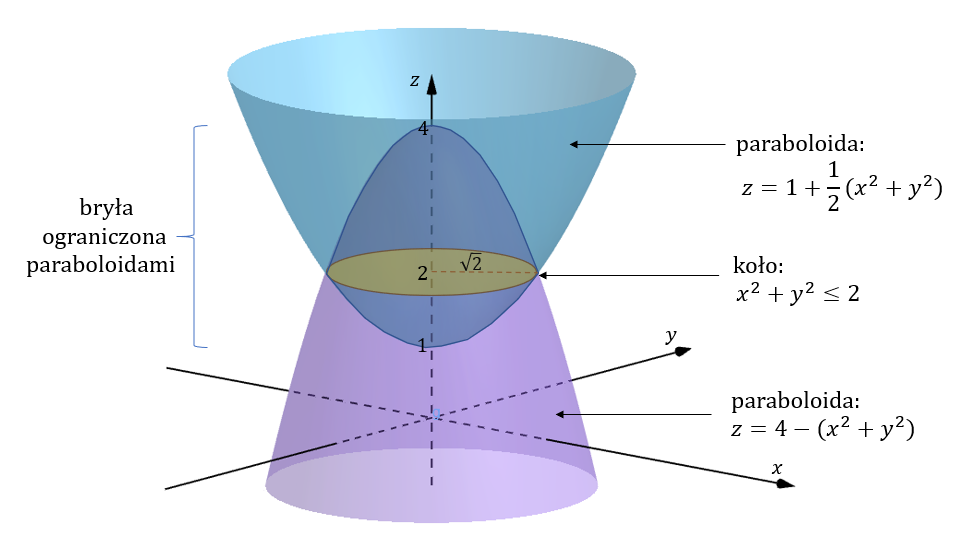 
Szukaną objętość bryły możemy tradycyjnie zapisać jako całkę potrójną po wszystkich trzech zmiennych: \[\iiint\limits_V dx\,dy\,dz\] Następnie przechodzimy na całkę podwójną, wprowadzając nowy obszar całkowania (wyznaczony przez nasz okrąg): \[D=\{(x,y)\in \mathbb{R}^2: x^2+y^2\le 2\}\] Teraz możemy zapisać: \[ \begin{split} &\iiint\limits_V dx\,dy\,dz=\\[6pt] =&\iint\limits_D \left(\int\limits_{1+\frac{1}{2}(x^2+y^2)}^{4-(x^2+y^2)}dz \right) dx\,dy=\\[6pt] =&\iint\limits_D \left(\left(4-(x^2+y^2)\right) - 1+\frac{1}{2}(x^2+y^2)\right)dx\,dy=\\[6pt] =&\iint\limits_D \left(3-\frac{3}{2}(x^2+y^2)\right)dx\,dy \end{split} \] Obszar \(D\) jest kołem o promieniu \(\sqrt{2}\), zatem możemy wykonać podstawienie na współrzędne biegunowe: \[\begin{cases} x=r\cos \varphi \\ y=r\sin \varphi \end{cases} \] gdzie \(r\in \langle0,\sqrt{2} \rangle\) oraz \(\varphi\in \langle 0,2\pi \rangle\). Jakobian tego przekształcenia, to tak samo jak w poprzednich przykładach: \[J=r\] Możemy teraz zdefiniować nowy obszar całkowania: \[\Delta=\{(r,\varphi)\in \mathbb{R}^2: 0\le r\le \sqrt{2},\ 0\le \varphi\le 2\pi \}\] i dalej na nim liczyć całkę: \[ \begin{split} &\iint\limits_D \left(3-\frac{3}{2}(x^2+y^2)\right)dx\,dy=\\[6pt] =&\iint\limits_\Delta (3 - \frac{3}{2} r^2\cos^2\varphi +r^2\sin^2\varphi)\cdot rdr\,d\varphi =\\[6pt] =&\iint\limits_\Delta (3 - \frac{3}{2} r^2)\cdot rdr\,d\varphi =\\[6pt] =&\int\limits_{0}^{2\pi}\left(\int\limits_{0}^{\sqrt{2}}\left(3r - \frac{3}{2} r^3\right)dr \right)d\varphi= \\[6pt] =&\int\limits_{0}^{2\pi}\left( \left.\left(\frac{3}{2}r^2-\frac{3}{8}r^4\right)\right\vert_0^{\sqrt{2}} \right)d\varphi= \\[6pt] =&\int\limits_{0}^{2\pi}\left( 3-\frac{3}{2} \right)d\varphi= \\[6pt] =&\int\limits_{0}^{2\pi}\left( \frac{3}{2} \right)d\varphi= \\[6pt] =&\left.\frac{3}{2}\varphi\right\vert_0^{2\pi}=\frac{3}{2}\cdot 2\pi-0=3\pi. \end{split} \] Zatem szukana objętość wynosi \(3\pi\).
Szukaną objętość bryły możemy tradycyjnie zapisać jako całkę potrójną po wszystkich trzech zmiennych: \[\iiint\limits_V dx\,dy\,dz\] Następnie przechodzimy na całkę podwójną, wprowadzając nowy obszar całkowania (wyznaczony przez nasz okrąg): \[D=\{(x,y)\in \mathbb{R}^2: x^2+y^2\le 2\}\] Teraz możemy zapisać: \[ \begin{split} &\iiint\limits_V dx\,dy\,dz=\\[6pt] =&\iint\limits_D \left(\int\limits_{1+\frac{1}{2}(x^2+y^2)}^{4-(x^2+y^2)}dz \right) dx\,dy=\\[6pt] =&\iint\limits_D \left(\left(4-(x^2+y^2)\right) - 1+\frac{1}{2}(x^2+y^2)\right)dx\,dy=\\[6pt] =&\iint\limits_D \left(3-\frac{3}{2}(x^2+y^2)\right)dx\,dy \end{split} \] Obszar \(D\) jest kołem o promieniu \(\sqrt{2}\), zatem możemy wykonać podstawienie na współrzędne biegunowe: \[\begin{cases} x=r\cos \varphi \\ y=r\sin \varphi \end{cases} \] gdzie \(r\in \langle0,\sqrt{2} \rangle\) oraz \(\varphi\in \langle 0,2\pi \rangle\). Jakobian tego przekształcenia, to tak samo jak w poprzednich przykładach: \[J=r\] Możemy teraz zdefiniować nowy obszar całkowania: \[\Delta=\{(r,\varphi)\in \mathbb{R}^2: 0\le r\le \sqrt{2},\ 0\le \varphi\le 2\pi \}\] i dalej na nim liczyć całkę: \[ \begin{split} &\iint\limits_D \left(3-\frac{3}{2}(x^2+y^2)\right)dx\,dy=\\[6pt] =&\iint\limits_\Delta (3 - \frac{3}{2} r^2\cos^2\varphi +r^2\sin^2\varphi)\cdot rdr\,d\varphi =\\[6pt] =&\iint\limits_\Delta (3 - \frac{3}{2} r^2)\cdot rdr\,d\varphi =\\[6pt] =&\int\limits_{0}^{2\pi}\left(\int\limits_{0}^{\sqrt{2}}\left(3r - \frac{3}{2} r^3\right)dr \right)d\varphi= \\[6pt] =&\int\limits_{0}^{2\pi}\left( \left.\left(\frac{3}{2}r^2-\frac{3}{8}r^4\right)\right\vert_0^{\sqrt{2}} \right)d\varphi= \\[6pt] =&\int\limits_{0}^{2\pi}\left( 3-\frac{3}{2} \right)d\varphi= \\[6pt] =&\int\limits_{0}^{2\pi}\left( \frac{3}{2} \right)d\varphi= \\[6pt] =&\left.\frac{3}{2}\varphi\right\vert_0^{2\pi}=\frac{3}{2}\cdot 2\pi-0=3\pi. \end{split} \] Zatem szukana objętość wynosi \(3\pi\). Można łatwo sprawdzić poprawność otrzymanego wyniku, korzystając z obserwacji, którą poczyniliśmy pod koniec przykładu pierwszego. Dzięki wyznaczonym ekstremom paraboloid możemy obliczyć objętość walca, w który wpisana jest nasza bryła: \[(4-1)\cdot (\sqrt{2})^2\pi=6\pi\] Objętość takiego walca powinna być dwukrotnie większa od szukanej objętości bryły i faktycznie tak jest, co potwierdza poprawność naszego wyniku.
Tematy nadrzędne i sąsiednie