Najnowsze filmy
Na tej stronie umieszczam moje najnowsze filmy.
Podczas pewnego turnieju piłkarskiego rozegrano \(50\) meczów. Na diagramie kołowym przedstawiono informacje o liczbie goli strzelonych w tych meczach. 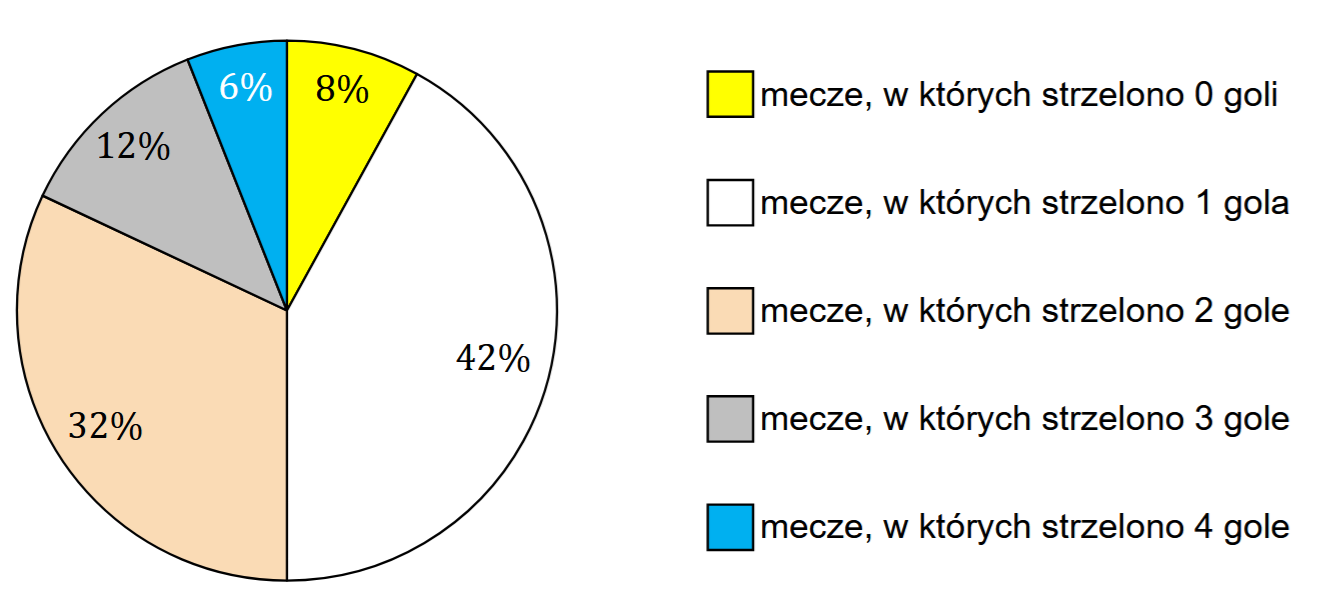

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Mediana liczb goli strzelonych w meczach tego turnieju jest równa A.\(1\)
B.\(1{,}5\)
C.\(2\)
D.\(2{,}5\)
Wykładowca akademicki, aby ustalić oceny semestralne, oblicza średnie ważone ocen otrzymanych przez studentów. Ocenom przypisano następujące wagi: 
- ocena z kartkówki – waga \(2\)
- ocena z projektu – waga \(3\)
- ocena za aktywność – waga \(4\)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Średnia ważona ocen uzyskanych przez Karolinę jest równa A.\(3{,}85\)
B.\(3{,}9\)
C.\(3{,}95\)
D.\(4\)
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Zdarzenie \(A\) polega na tym, że wylosujemy liczbę, która jest wielokrotnością liczby \(34\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Prawdopodobieństwo zdarzenia \(A\) jest równe A.\(\frac{1}{89}\)
B.\(\frac{2}{89}\)
C.\(\frac{1}{90}\)
D.\(\frac{2}{90}\)
Rysunek drwala składa się z sześciu obszarów ponumerowanych liczbami od 1 do 6. Każdy z tych obszarów należy pokolorować jednym z siedmiu kolorów w taki sposób, aby każde dwa obszary graniczące ze sobą miały różny kolor. 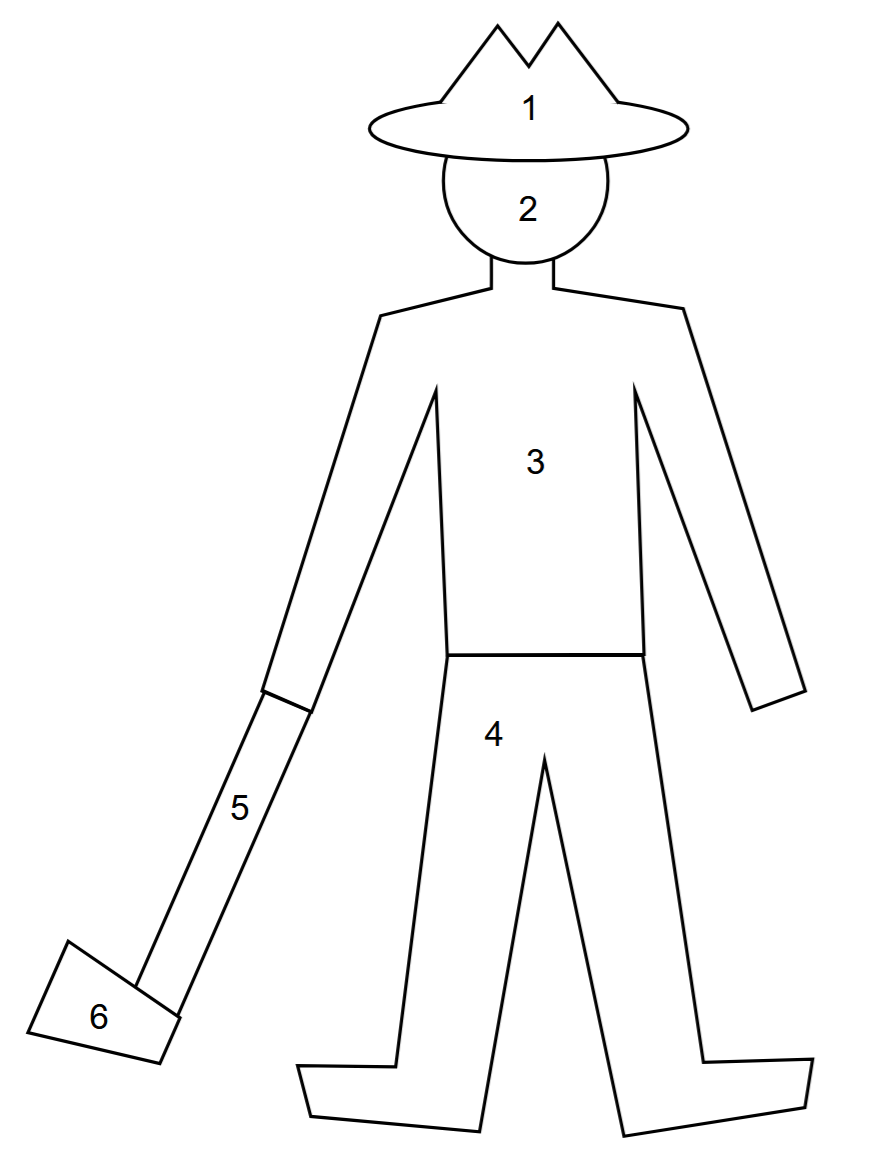

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wszystkich takich sposobów pokolorowania drwala jest A.\(7\cdot 6^5\)
B.\(7^3\cdot 6^3\)
C.\(7\cdot 6\)
D.\(7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\)
Pole powierzchni całkowitej walca \(C_1\) jest równe \(12\pi\), a objętość tego walca jest równa \(4\pi\). Walec \(C_2\) jest podobny do walca \(C_1\) w skali \(k=2\).
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Pole powierzchni całkowitej walca \(C_2\) jest równe \(48\pi\). | P | F |
| Objętość walca \(C_2\) jest równa \(32\pi\). | P | F |
W kartezjańskim układzie współrzędnych \((x,y)\) punkty \(A=(-3,0)\) oraz \(C=(5,6)\) są końcami przekątnej kwadratu \(ABCD\). Kwadrat \(A'B'C'D'\) jest obrazem kwadratu \(ABCD\) w symetrii osiowej względem osi \(Oy\).
Wyznacz równanie okręgu opisanego na kwadracie \(A'B'C'D'\). Zapisz obliczenia.
Dany jest sześcian \(ABCDEFGH\). Pole trójkąta \(ACH\) jest równe \(4\sqrt{3}\). 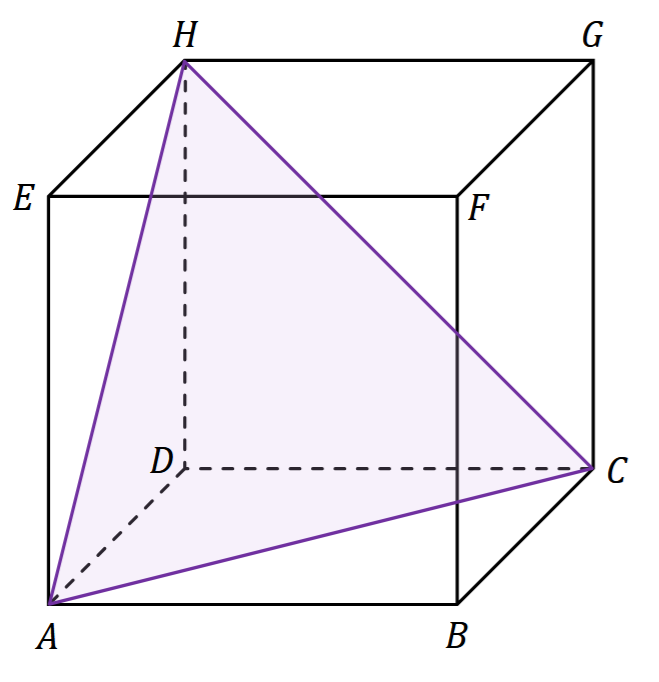

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość krawędzi tego sześcianu jest równa A.\(2\)
B.\(2\sqrt{2}\)
C.\(4\)
D.\(4\sqrt{2}\)
Dany jest ostrosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość \(12\). Ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze \(30^\circ\).
Oblicz objętość tego ostrosłupa. Zapisz obliczenia.
Sześciokąt foremny wpisano w koło o promieniu \(1\). 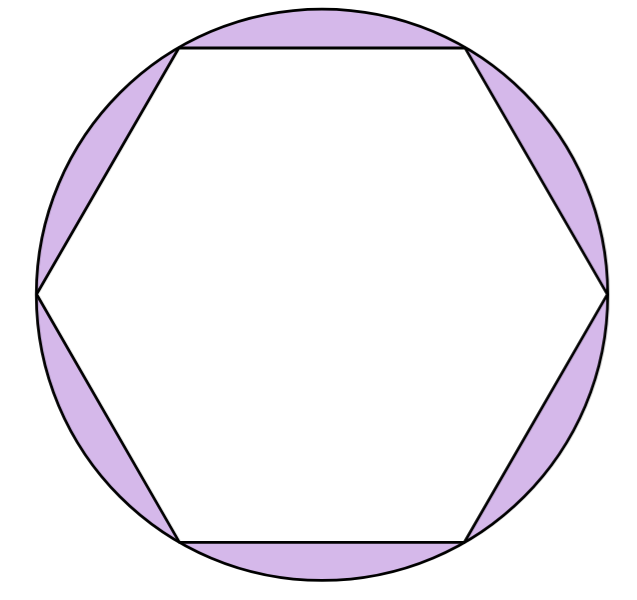

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole zacieniowanej figury jest równe A.\(\pi-\frac{\sqrt{3}}{4}\)
B.\(\pi-\frac{3\sqrt{3}}{2}\)
C.\(\frac{\pi-\sqrt{3}}{4}\)
D.\(\frac{\pi-3\sqrt{3}}{2}\)
W kartezjańskim układzie współrzędnych \((x,y)\) proste \(k\) oraz \(l\) są określone równaniami \[ k:(m-1)x+3y+5=0,\qquad l:6x+y+7=0. \]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Proste \(k\) oraz \(l\) są równoległe, gdy liczba \(m\) jest równa A.\(6\)
B.\(7\)
C.\(18\)
D.\(19\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
W każdym trójkącie środek okręgu wpisanego w ten trójkąt leży w punkcie przecięcia się A.dwusiecznych kątów tego trójkąta.
B.symetralnych boków tego trójkąta.
C.środkowych tego trójkąta.
D.wysokości tego trójkąta.
Punkty \(A,B,C,D\) leżą na okręgu o środku w punkcie \(O\). Punkt \(K\) jest punktem przecięcia cięciwy \(AC\) i średnicy \(BD\). Kąt \(COB\) jest prosty, a kąt \(AKD\) ma miarę \(78^\circ\). 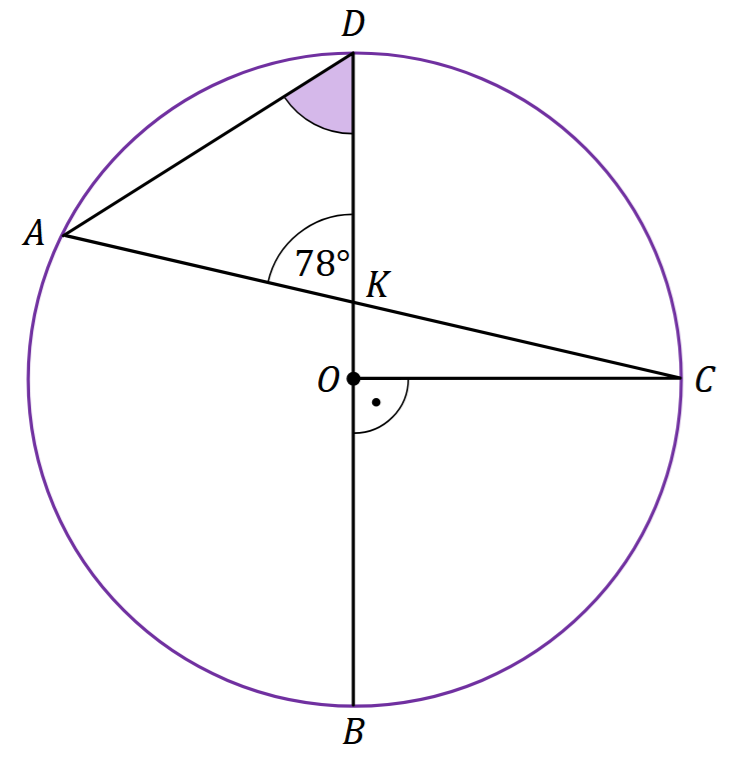

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miara kąta ostrego \(BDA\) jest równa A.\(45^\circ\)
B.\(51^\circ\)
C.\(57^\circ\)
D.\(78^\circ\)
Dany jest trapez równoramienny \(ABCD\) o podstawach \(AB\) i \(CD\), w którym \(|AB|=2\cdot|CD|\). Przekątna \(AC\) tego trapezu jest zawarta w dwusiecznej kąta \(DAB\).
Wykaż, że w tym trapezie miara kąta \(DAB\) jest równa \(60^\circ\).
Ciąg geometryczny \((a_n)\), określony dla każdej liczby naturalnej \(n\ge 1\), jest malejący. Wyrazy tego ciągu spełniają warunek \(a_6=25\cdot a_8\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Iloraz ciągu \((a_n)\) jest równy A.\(\frac{1}{5}\)
B.\(\left(-\frac{1}{5}\right)\)
C.\(5\)
D.\((-5)\)
Kąt o mierze \(\alpha\) jest rozwarty oraz \(\sin\alpha=\frac{1}{\sqrt{3}}\).
Oblicz wartość wyrażenia \(\frac{3\sin\alpha}{\operatorname{tg} \alpha}\). Zapisz obliczenia.
Zadanie 18. (0–1)
Dany jest trójkąt prostokątny \(ABC\), w którym bok \(BC\) jest przeciwprostokątną oraz \(|AC|=6\). Tangens kąta \(BCA\) jest równy \(\frac{3}{2}\). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Odcinek \(AB\) ma długość A.\(3\)
B.\(4\)
C.\(9\)
D.\(\sqrt{117}\)
Ciąg \((a_n)\) jest określony wzorem \[ a_n=\frac{3n+9}{n+1} \] dla każdej liczby naturalnej \(n\ge 1\).
Wyznacz wszystkie wartości \(x\), dla których trzywyrazowy ciąg \((a_5,\;2x^2,\;3x^2+5)\) jest arytmetyczny. Zapisz obliczenia.
Ciąg \((a_n)\) jest określony następująco: \[ \begin{cases} a_1=5\\ a_{n+1}=a_n+2 \quad \text{dla } n\ge 1 \end{cases} \]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Suma stu początkowych kolejnych wyrazów ciągu \((a_n)\) jest równa A.\(203\)
B.\(205\)
C.\(10400\)
D.\(10500\)
Funkcja kwadratowa \(f\) jest określona wzorem \(f(x)=-16x^2+40x+11\). W kartezjańskim układzie współrzędnych \((x,y)\) wykresem funkcji \(f\) jest parabola o wierzchołku w punkcie \(C\). Ta parabola przecina oś \(Ox\) w punktach \(A\) oraz \(B\). Oblicz pole trójkąta \(ABC\). Zapisz obliczenia.
Wielkości \(x\) oraz \(y\) zestawione w tabeli poniżej są odwrotnie proporcjonalne.
| \(x\) | 18 | 24 |
| \(y\) | 9 | \(a\) |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(a\) jest równa A.\(3\)
B.\(6{,}75\)
C.\(12\)
D.\(15\)
Rozwiązaniem układu równań \[ \begin{cases} 20x+20y=1\\ 26x-26y=1 \end{cases} \] jest para liczb: \(x=x_0,\;y=y_0\).
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Suma \(x_0+y_0\) jest liczbą dodatnią. | P | F |
| Iloczyn \(x_0\cdot y_0\) jest liczbą dodatnią. | P | F |
Funkcja liniowa \(f\) jest określona wzorem \(f(x)=(k+2)x+(k-3)\), gdzie \(k\) jest liczbą rzeczywistą. Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Funkcja \(f\) jest malejąca dla każdej liczby \(k\) należącej do przedziału \((-\infty,2)\). | P | F |
| W kartezjańskim układzie współrzędnych \((x,y)\) wykres funkcji \(f\) przechodzi przez punkt \((0,1)\) dla \(k=4\). | P | F |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Równanie \(2x(x^2-3)(x^2+2x+3)=0\) w zbiorze liczb rzeczywistych ma dokładnie A.jedno rozwiązanie.
B.dwa rozwiązania.
C.trzy rozwiązania.
D.pięć rozwiązań.
Rozwiąż nierówność \((x-3)(x+5)>9\). Zapisz obliczenia.
Wykaż, że liczba \(2501^4-2499^4\) jest podzielna przez \(10000\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdej liczby rzeczywistej \(x\) różnej od \((-10)\) oraz różnej od \(0\) wartość wyrażenia \(\frac{x^2+20x+100}{x^3}\cdot\frac{x^2}{x+10}\) jest równa wartości wyrażenia A.\(20x+10\)
B.\(\frac{1}{x}\)
C.\(\frac{x+10}{x}\)
D.\(\frac{x^2+30}{x}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\log_{8}\sqrt[5]{2}\) jest równa A.\(\frac{1}{15}\)
B.\((-15)\)
C.\(\frac{3}{5}\)
D.\(\frac{5}{3}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\frac{3^{10}\cdot 9^{20}}{27^{15}}\) jest równa A.\(1\)
B.\(3^5\)
C.\(3^{15}\)
D.\(3^{45}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\frac{\sqrt[3]{50}\cdot\sqrt[3]{-15}}{\sqrt[3]{2}\cdot\sqrt[3]{3}}\) jest równa A.\(5\)
B.\((-5)\)
C.\(5\sqrt[3]{5}\)
D.\((-5\sqrt[3]{5})\)
Liczby \(x\) oraz \(y\) są całkowite i dodatnie. W wyniku dzielenia liczby \(x\) przez liczbę \(y\) otrzymano iloraz \(20\) i resztę \(26\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\frac{x}{y}\) jest równa A.\(26+\frac{20}{x}\)
B.\(26+\frac{20}{y}\)
C.\(20+\frac{26}{x}\)
D.\(20+\frac{26}{y}\)
Rozwiąż równanie \[ \log _{x}(27)=2+\log _{3}(x) \] gdzie \(x \in(0,1) \cup(1,+\infty)\). Zapisz obliczenia.
Zagadnienia CKE omawiane w lekcji:
- Definicja ciągu geometrycznego.
- Obliczanie wyrazów i ilorazu ciągu geometrycznego.
- Wyznaczanie wzoru na \(n\)-ty wyraz ciągu geometrycznego.
- 3 kolejne wyrazy ciągu geometrycznego.
- Wzór na sumę \(n\) początkowych wyrazów ciągu geometrycznego.
- Wykazywanie, że ciąg jest geometryczny.
Do zdobycia na maturze: 1-2 punkty.
Szansa pojawienia się na maturze: 90%.
Zagadnienia CKE omawiane w lekcji:
- Definicja ciągu arytmetycznego.
- Obliczanie wyrazów ciągu określonego wzorem ogólnym.
- Wzór na \(n\)-ty wyraz ciągu arytmetycznego.
- 3 kolejne wyrazy ciągu arytmetycznego
- Wzór na sumę \(n\) początkowych wyrazów ciągu arytmetycznego.
- Wykazywanie, że ciąg jest arytmetyczny
Do zdobycia na maturze: 1-4 punkty.
Szansa pojawienia się na maturze: 90%.
W tym materiale dokładnie analizuję i omawiam wszystkie najważniejsze zagadnienia jakie trzeba umieć do matury rozszerzonej z matematyki. W materiale znajdziesz:
- Zestawienie wszystkich ostatnich oficjalnych arkuszy z lat 2023, 2024 i 2025 z oznaczeniem jaki typ zadania pojawił się w którym arkuszu.
- Ocenę szansy pojawiania się danego typu zadania na najbliższej maturze.
- Tier listę wszystkich zagadnień, czyli oznaczenie z których zagadnień możesz zdobyć najwięcej punktów najmniejszym wysiłkiem. Kolejność od najlepszy do najgorszych, to: S+, S, A, B, C.
W tym materiale dokładnie analizuję i omawiam wszystkie najważniejsze zagadnienia jakie trzeba umieć do matury podstawowej z matematyki. W materiale znajdziesz:
- Zestawienie wszystkich ostatnich oficjalnych arkuszy z lat 2024 i 2025 z oznaczeniem jaki typ zadania pojawił się w którym arkuszu
- Ocenę szansy pojawiania się danego typu zadania na najbliższej maturze
- Tier listę wszystkich zagadnień, czyli oznaczenie z których zagadnień możesz zdobyć najwięcej punktów najmniejszym wysiłkiem. Kolejność od najlepszy do najgorszych, to: S+, S, A, B, C
W tej lekcji pokazuję jak szybko znajdować postać iloczynową wielomianu na przykładach:
- \(x^3+x^2-16 x+20=0\)
- \(2 x^3+5 x^2-x-6=0\)
Kąt dwuścienny zawarty między sąsiednimi ścianami bocznymi ostrosłupa prawidłowego czworokątnego ma miarę \(2\alpha\). Wyznacz sinus kąta nachylenia ściany bocznej tego ostrosłupa do jego podstawy.
W wyniku przeprowadzonej analizy pewnego przedsiębiorstwa ustalono, że zysk z produkcji jest zależny od liczby zatrudnionych pracowników i wyraża się następującym wzorem: \[ Z(x)=\frac{17}{29}x(130-x) \] gdzie:
\(x\) - liczba zatrudnionych pracowników
\(Z\) - miesięczny zysk z produkcji przedsiębiorstwa
\(x\) - liczba zatrudnionych pracowników
\(Z\) - miesięczny zysk z produkcji przedsiębiorstwa
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miesięczny zysk z produkcji przedsiębiorstwa będzie największy, jeżeli liczba zatrudnionych pracowników wyniesie A.\(58\)
B.\(65\)
C.\(70\)
D.\(87\)
Program komputerowy wykonał \(99\) losowań liczb, za każdym razem losując jedną liczbę ze zbioru \(\{0, 1, 2, 3\}\). Wyniki losowań zebrano w tabeli: 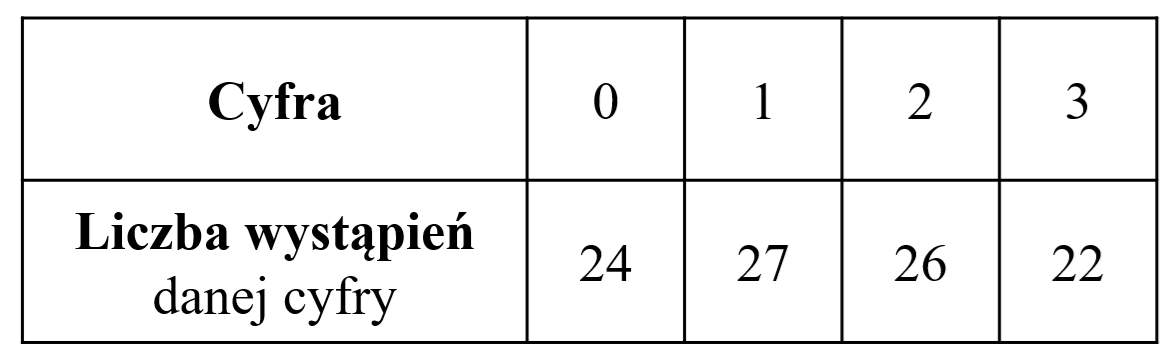 Mediana zbioru wylosowanych liczb jest równa
Mediana zbioru wylosowanych liczb jest równa
 Mediana zbioru wylosowanych liczb jest równa
Mediana zbioru wylosowanych liczb jest równa A.\( 1 \)
B.\( 1,5 \)
C.\( 2 \)
D.\( 2,5 \)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Doświadczenie losowe polega na trzykrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od 1 do 6. Zdarzenie \(A\) polega na tym, że iloczyn liczb wyrzuconych oczek jest równy \(8\). Prawdopodobieństwo zdarzenia \(A\) jest równe A.\(\dfrac{1}{216}\)
B.\(\dfrac{6}{216}\)
C.\(\dfrac{7}{216}\)
D.\(\dfrac{8}{216}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wszystkich liczb naturalnych czterocyfrowych podzielnych przez \(5\), w zapisie których cyfry nie powtarzają się jest A.\( 2\cdot 9\cdot 8\cdot 7\)
B.\( 2\cdot 8\cdot 8\cdot 7\)
C.\( 9\cdot 8\cdot 7 + 8\cdot 7\cdot 6 \)
D.\( 9\cdot 8\cdot 7 + 8\cdot 8\cdot 7\)
Tworząca stożka ma długość \(10\). Kąt rozwarcia stożka ma miarę \(90^{\circ}\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Objętość tego stożka jest równa A.\(250\sqrt{2}\pi\)
B.\(\frac{250\sqrt{2}}{3}\pi\)
C.\(\frac{500\sqrt{2}}{3}\pi\)
D.\(500\sqrt{2}\pi\)
Pole podstawy ostrosłupa prawidłowego trójkątnego jest równe \(\frac{15\sqrt{3}}{4}\). Krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem \(\alpha \), takim, że \(\cos \alpha =\frac{1}{3}\).
Oblicz objętość tego ostrosłupa. Zapisz obliczenia.
W kartezjańskim układzie współrzędnych \((x, y)\) dane są cztery okręgi: \(o_{1}, o_{2}, o_{3}, o_{4}\), o równaniach: \[ \begin{aligned} & o_{1}:(x-1)^{2}+(y-2)^{2}=2 \\[6pt] & o_{2}:(x+3)^{2}+(y+1)^{2}=8 \\[6pt] & o_{3}:(x-3)^{2}+(y-2)^{2}=9 \\[6pt] & o_{4}:(x-2)^{2}+(y+3)^{2}=10 \end{aligned} \]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Okręgiem, który ma dokładnie \(3\) punkty wspólne z osiami układu współrzędnych \((x, y)\), jest A.\(o_{1}\)
B.\(o_{2}\)
C.\(o_{3}\)
D.\(o_{4}\)
W kartezjańskim układzie współrzędnych \((x, y)\) dane są dwa punkty \(A=(1, 0)\) oraz \(B=(-2, 1)\), które są wierzchołkami rombu \(ABCD\). Osią symetrii rombu \(ABCD\) jest oś \(OX\) układu współrzędnych.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole tego rombu jest równe A.\( 6 \)
B.\( 9 \)
C.\( 12 \)
D.\( 18 \)
W trójkącie prostokątnym \(ABC\) poprowadzono wysokość \(CD\) z wierzchołka kąta prostego, która podzieliła przeciwprostokątną \(BC\) na odcinki długości \(9\) i \(3\) (zobacz rysunek). 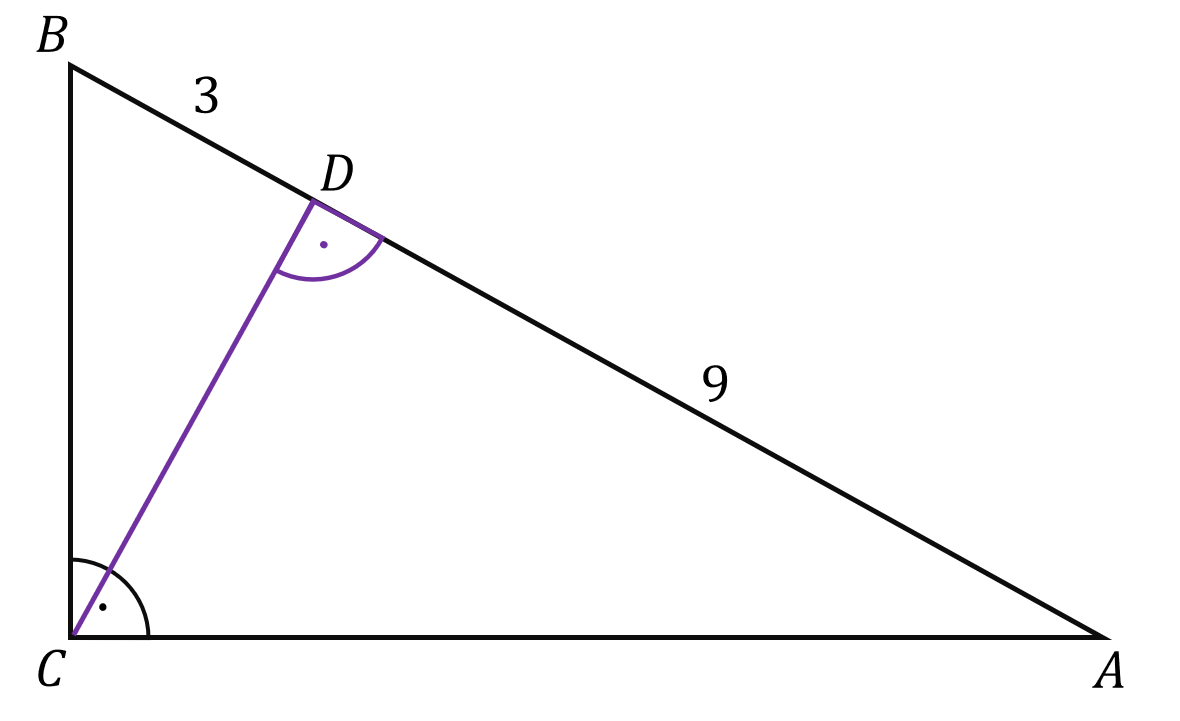

Oblicz pole i obwód trójkąta \(ABC\). Zapisz obliczenia.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
W kartezjańskim układzie współrzędnych \((x, y)\) proste \(k\) oraz \(l\) są określone równaniami \[ \begin{aligned} k:&\; y=(2m+1)\,x+m\\ l:&\; y=(m^2+1)x-m \end{aligned} \] Proste \(k\) oraz \(l\) nie mają punktów wspólnych, gdy liczba \(m\) jest równa A.\((-2)\)
B.\(0\)
C.\(1\)
D.\(2\)
Pole koła wpisanego w trójkąt równoboczny \(ABC\) jest równe \(36\pi\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole trójkąta \(ABC\) jest równe A.\( 27\sqrt{3} \)
B.\( 54\sqrt{3} \)
C.\( 108\sqrt{3} \)
D.\( 216\sqrt{3} \)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Kąt \(\alpha\) jest ostry i spełnia warunek \[\,\mathrm{tg}\,\alpha - \cos^{2} \alpha = \frac{1}{3\cos \alpha }+\sin^2\alpha-1\] Sinus kąta \(\alpha\) jest równy A.\(\dfrac{1}{3}\)
B.\(\dfrac{\sqrt{3}}{2}\)
C.\(\dfrac{1}{4}\)
D.\(\dfrac{\sqrt{3}}{5}\)
Dany jest ciąg arytmetyczny \(\left(a_{n}\right)\) określony dla każdej liczby naturalnej \(n \geq 1\), w którym \(a_{4}=\sqrt{2}\) oraz \(a_{8}=5\sqrt{2}\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Szósty wyraz ciągu \(\left(a_{n}\right)\) jest równy A.\(2\)
B.\(2\sqrt{2}\)
C.\(3\sqrt{2}\)
D.\(\frac{\sqrt{2}}{2}\)
Wyznacz wszystkie wartości parametru \(m\), dla którego trzywyrazowy ciąg \[ \left(2m-1,\ m,\ 2m+1\right) \] jest geometryczny. Zapisz obliczenia.
Ciąg \(\left(a_{n}\right)\) jest określony następująco: \[ \left\{\begin{array}{l} a_{1}=-1 \\ a_{n+1}=n^2+a_{n} \end{array} \right. \] dla każdej liczby naturalnej \(n \geq 1\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Suma trzech pierwszych wyrazów tego ciągu jest równa A.\(0\)
B.\(1\)
C.\(2\)
D.\(3\)
Funkcja liniowa \(f\) jest określona wzorem \(f(x)=(10-2k)x+\frac{k}{5}\), gdzie \(k\) jest liczbą rzeczywistą. Funkcja \(f\) jest malejąca.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(k\) należy do przedziału A.\((-\infty,-5)\)
B.\((-5,5)\)
C.\(\left(-\frac{1}{5}, \frac{1}{5}\right)\)
D.\((5,+\infty)\)
Rozwiąż równanie \[\frac{x}{2x-1}=1-\frac{3-x}{3+x}\] Zapisz konieczne założenie i obliczenia.
Funkcja \(f\) jest określona następująco: \[ f(x)= \begin{cases} 4 & \text{dla } x\in[-5,-2)\\ -2x & \text{dla } x\in[-2,1]\\ x-\frac{5}{2} & \text{dla } x\in(1,4) \end{cases} \] Wykres funkcji \(y=f(x)\) przedstawiono w kartezjańskim układzie współrzędnych \((x, y)\) na rysunku poniżej. 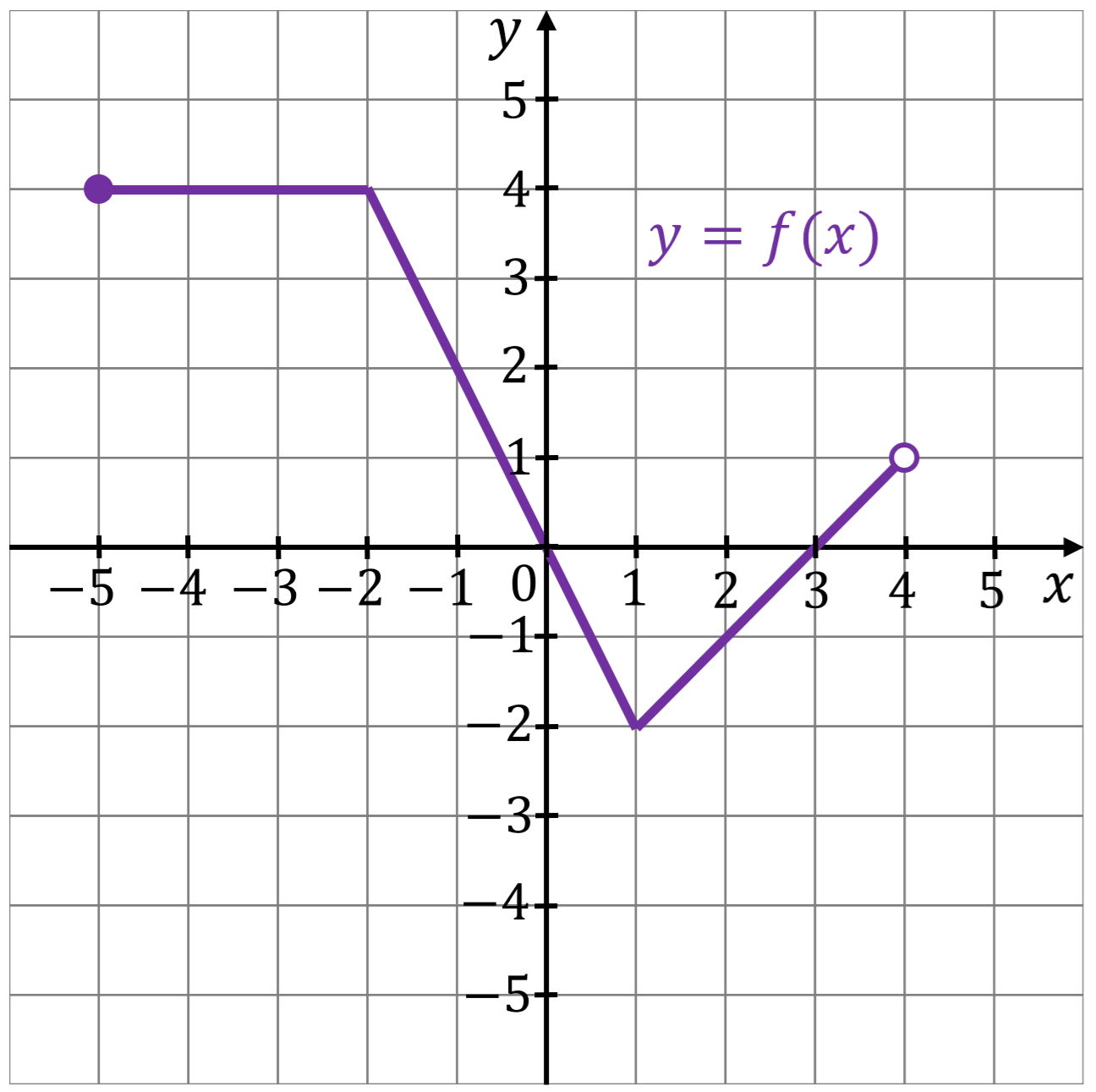

Uzupełnij zdania. Wpisz odpowiednie przedziały w wykropkowanych miejscach, aby zdania były prawdziwe.
- Dziedziną funkcji \(f\) jest przedział …………………… .
- Zbiorem wszystkich argumentów, dla których funkcja \(f\) jest stała, jest przedział …………………… .
- Suma miejsc zerowych funkcji \(f\) jest równa …………………… .
- Liczba rozwiązań równania \(f(x)=-1,(3)\) jest równa …………………… .
Serwis streamingowy wypłacił dwóm artystom łącznie \(180\ 000\) złotych za odtworzenia ich utworów 2024 roku. W roku 2025 wynagrodzenie jednego artysty wzrosło o \(20\%\), drugiego spadło o \(30\%\), ale ich łączne wynagrodzenie wyniosło tyle samo co w roku poprzednim.
Oblicz, jakie wynagrodzenia otrzymali obaj artyści w 2025 roku. Zapisz obliczenia.
Rozwiąż nierówność \[ x(x+11)\le x-25 \] Zapisz obliczenia.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zbiorem wszystkich rozwiązań nierówności \[ \frac{2-x}{4}>\;x-\frac{1}{2} \] jest przedział A.\(\left(-\infty,\,\frac{4}{5}\right)\)
B.\(\left(-\infty,\,\frac{2}{3}\right)\)
C.\(\left(\frac{2}{3},\,+\infty\right)\)
D.\(\left(\frac{4}{5},\,+\infty\right)\)
Wykaż, że dla każdej liczby całkowitej \(a\), która przy dzieleniu przez \(7\) daje resztę \(2\), oraz dla każdej liczby całkowitej \(b\), która przy dzieleniu przez \(7\) daje resztę \(5\), liczba \(a^{2}+2b^{2}+2\) jest podzielna przez \(7\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Średnia arytmetyczna wszystkich rozwiązań równania \((2x+2)(3x-6)(5x+15)=0\) jest równa A.\(\left(-\frac{2}{3}\right)\)
B.\(\left(-\frac{1}{3}\right)\)
C.\(0\)
D.\(\frac{1}{3}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\log_{5}105-3\log_{5}\sqrt[3]{21}\) jest równa A.\(-1\)
B.\(0\)
C.\(1\)
D.\(\log_{5}\frac{105}{\sqrt[3]{21}}\)
Dane są liczby \(a=|1+\sqrt{2}|\) oraz \(b=|1-\sqrt{2}|\).
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Liczba \(a+b\) jest liczbą całkowitą. | P | F |
| Liczba \(a\cdot b\) jest liczbą całkowitą. | P | F |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\frac{(5\sqrt{2}+\sqrt{18})^2}{4^{4}\cdot 8^8}\) jest równa A.\(2^{-30}\)
B.\(2^{-25}\)
C.\(2^{-15}\)
D.\(2^{-10}\)
Zagadnienia CKE omawiane w lekcji:
- Prawdopodobieństwo warunkowe
- Prawdopodobieństwo całkowite
Do zdobycia na maturze: 3 punkty.
Szansa pojawienia się na maturze: 30%.
Zagadnienia CKE omawiane w lekcji:
- Prawdopodobieństwo w modelu klasycznym.
- Obliczenia prawdopodobieństwa z wykorzystaniem zdarzenia przeciwnego.
- Zastosowania wzoru na prawdopodobieństwo sumy zdarzeń.
- Powtórka i rozszerzenie sytuacji z kombinatoryki.
Do zdobycia na maturze: 3 punkty.
Szansa pojawienia się na maturze: 30%.
Materiał dodatkowy z kombinatoryki o wzorze Stirlinga i zasadzie włączeń i wyłączeń.
Znajomość technik prezentowanych w tym materiale nie powinna być obecnie potrzebna na maturze rozszerzonej.
Materiał dla chętnych.
Znajomość technik prezentowanych w tym materiale nie powinna być obecnie potrzebna na maturze rozszerzonej.
Materiał dla chętnych.
Szansa pojawienia się na maturze: 0%.
Zagadnienia CKE omawiane w lekcji:
- Reguła mnożenia i dodawania, permutacje, kombinacje i wariacje.
- Rozwiązywanie przypadków wymagających rozważenia złożonego modelu zliczania elementów.
- Zastosowanie współczynnika dwumianowego (symbol Newtona) i jego własności przy rozwiązywaniu problemów kombinatorycznych.
- Omówienie ponad 30 sytuacji kombinatorycznych i różnych sposobów rozwiązywania problemów, a także prezentacja sprytnych technik z poziomu ponadrozszerzonego (matematyka dyskretna).
Do zdobycia na maturze: 4 punkty.
Szansa pojawienia się na maturze: 50%.
Zagadnienia CKE omawiane w lekcji:
- wyznaczanie przekrojów sześcianu i ostrosłupów prawidłowych oraz obliczanie ich pól, także z wykorzystaniem trygonometrii.
Do zdobycia na maturze: 5 punktów.
Szansa pojawienia się na maturze: 60%.
Omówienie wszystkich zadań z arkusza matury próbnej od wydawnictwa Operon 2025/2026.
Omówienie wszystkich zadań z arkusza rozszerzonego matury próbnej od wydawnictwa Operon 2025/2026.
Czas lekcji: 60 min.
Tematy nadrzędne i sąsiednie