Matura 2019 maj PR

Dla dowolnych liczb \(x\gt 0,\ x\ne 1,\ y\gt 0,\ y\ne 1\) wartość wyrażenia \(\left(\log_{\frac{1}{x}}y\right)\cdot \left(\log_{\frac{1}{y}}x\right)\) jest równa

Liczba \(\cos^{2}105^\circ -\sin^{2} 105^\circ \) jest równa

Na rysunku przedstawiono fragment wykresu funkcji \(y = f(x)\), który jest złożony z dwóch półprostych \(AD\) i \(CE\) oraz dwóch odcinków \(AB\) i \(BC\), gdzie \(A = (-1, 0)\), \(B = (1, 2)\), \(C = (3, 0)\), \(D = (-4, 3)\), \(E = (6, 3)\). 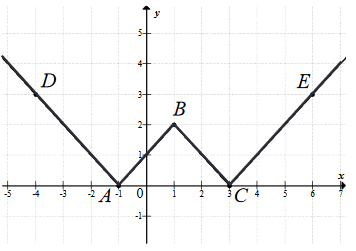Wzór funkcji \(f\) to

Zdarzenia losowe \(A\) i \(B\) zawarte w \(\Omega\) są takie, że prawdopodobieństwo \(P(B')\) zdarzenia \(B'\), przeciwnego do zdarzenia \(B\), jest równe \(\frac{1}{4}\). Ponadto prawdopodobieństwo warunkowe \(P(A|B) = \frac{1}{5}\). Wynika stąd, że

Oblicz granicę \(\lim_{n \to \infty} \Biggl( \frac{9n^3 + 11n^2}{7n^3 + 5n^2 + 3n + 1} - \frac{n^2}{3n^2 + 1}\Biggl)\) Wpisz w poniższe kratki – od lewej do prawej – trzy kolejne cyfry po przecinku rozwinięcia dziesiętnego otrzymanego wyniku.

Rozważamy wszystkie liczby naturalne pięciocyfrowe zapisane przy użyciu cyfr \(1\), \(3\), \(5\), \(7\), \(9\), bez powtarzania jakiejkolwiek cyfry. Oblicz sumę wszystkich takich liczb.

Punkt \(P = (10, 2429)\) leży na paraboli o równaniu \(y = 2x^2 + x + 2219\). Prosta o równaniu kierunkowym \(y = ax + b\) jest styczna do tej paraboli w punkcie \(P\). Oblicz współczynnik \(b\).

Udowodnij, że dla dowolnych dodatnich liczb rzeczywistych \(x\) i \(y\), takich że \(x \lt y\), i dowolnej dodatniej liczby rzeczywistej \(a\), prawdziwa jest nierówność \(\frac{x + a}{y + a} + \frac{y}{x} \gt 2\).

Dany jest trójkąt równoramienny \(ABC\), w którym \(|AC| = |BC|\). Na ramieniu \(AC\) tego trójkąta wybrano punkt \(M (M \ne A\) i \(M \ne C)\), a na ramieniu \(BC\) wybrano punkt \(N\), w taki sposób, że \(|AM| = |CN|\). Przez punkty \(M\) i \(N\) poprowadzono proste prostopadłe do podstawy \(AB\) tego trójkąta, które wyznaczają na niej punkty \(S\) i \(T\). Udowodnij, że \(|ST| = \frac{1}{2}|AB|\).

Punkt \(D\) leży na boku \(AB\) trójkąta \(ABC\) oraz \(|AC| = 16\), \(|AD| = 6\), \(|CD| = 14\) i \(|BC| = |BD|\). Oblicz obwód trójkąta \(ABC\).

Dane są okręgi o równaniach \(x^2 + y^2 - 12x - 8y + 43 = 0\) i \(x^2 + y^2 - 2ax + 4y + a^2 - 77 = 0\). Wyznacz wszystkie wartości parametru \(a\), dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.

Trzywyrazowy ciąg \((a, b, c)\) o wyrazach dodatnich jest arytmetyczny, natomiast ciąg \(\Biggl(\frac{1}{a}, \frac{2}{3b}, \frac{1}{2a + 2b + c}\Biggl)\) jest geometryczny. Oblicz iloraz ciągu geometrycznego.

Wielomian określony wzorem \(W(x) = 2x^3 + (m^3 + 2)x^2 - 11x - 2(2m + 1)\) jest podzielny przez dwumian \((x - 2)\) oraz przy dzieleniu przez dwumian \((x + 1)\) daje resztę \(6\). Oblicz \(m\) i dla wyznaczonej wartości \(m\) rozwiąż nierówność \(W(x) \le 0\).

Rozwiąż równanie \((\cos x) \Biggl[ \sin \biggl(x - \frac{\pi}{3} \biggl) + \sin \biggl(x + \frac{\pi}{3} \biggl)\Biggl] = \frac{1}{2}\sin x\).

Rozważmy wszystkie graniastosłupy prawidłowe trójkątne o objętości \(V = 2\). Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.