Matura 2017 listopad

Drukuj

Poziom podstawowy

Na tej znajdują się rozwiązania zadań matury próbnej organizowanej przez Wydawnictwo Operon 22 listopada 2017.

Szybka nawigacja do zadania numer: 5 10 15 20 25 30 .

Liczba \(\log_2\frac{1}{\sqrt{8}}\) jest równa:

A.\( -\frac{3}{2} \)

B.\( \frac{3}{2} \)

C.\( \frac{1}{3} \)

D.\( -\frac{1}{3} \)

Liczba \(a=\frac{14\sqrt{2}}{\sqrt{2}-3}\) należy do przedziału:

A.\( (-\infty ,-13) \)

B.\( \langle -13,-12) \)

C.\( (12,13\rangle \)

D.\( (13,+\infty ) \)

Reszta z dzielenia liczby naturalnej \(x\) przez \(9\) jest równa \(7\). Reszta z dzielenia kwadratu tej liczby przez \(9\) jest równa:

A.\( 2 \)

B.\( 4 \)

C.\( 6 \)

D.\( 8 \)

Prosta \(l\) przechodzi przez punkty \(A=(6,-7), B=(-10,3)\). Prosta \(k\) jest symetralną odcinka \(AB\). Współczynnik kierunkowy prostej \(k\) jest równy:

A.\( -\frac{8}{5} \)

B.\( \frac{8}{5} \)

C.\( \frac{5}{8} \)

D.\( -\frac{5}{8} \)

Dany jest ciąg \((a_n)\) o wyrazie ogólnym \(a_n=\frac{2n+1}{n+3}\). Liczby \(a_3,a_5\) są wyrazami tego ciągu, a liczby \((a_3,x,a_5)\) tworzą ciąg arytmetyczny. Liczba \(x\) jest równa:

A.\( x=\frac{61}{48} \)

B.\( x=\frac{61}{96} \)

C.\( x=\frac{69}{96} \)

D.\( x=\frac{69}{48} \)

Dana jest funkcja określona wzorem \(y=x^2-4\sqrt{3}x+12\). Trzecia potęga jedynego miejsca zerowego tej funkcji to liczba:

A.\( 8\sqrt{3} \)

B.\( 24 \)

C.\( 24\sqrt{3} \)

D.\( 12 \)

Do wykresu funkcji wykładniczej \(f(x)=\left(\frac{1}{4}\right)^x\) należy punkt

A.\( A=\left(-\frac{1}{2},-2\right) \)

B.\( A=\left(-\frac{1}{2},2\right) \)

C.\( A=\left(2,\frac{1}{2}\right) \)

D.\( A=\left(2,-\frac{1}{2}\right) \)

Dany jest ciąg geometryczny o wyrazach różnych od \(0\). Suma siódmego i ósmego wyrazu tego ciągu jest równa \(0\). Oznacza to, że suma tysiąca początkowych wyrazów tego ciągu jest równa:

A.\( 1000a_1 \)

B.\( 1001a_1 \)

C.\( 10 \)

D.\( 0 \)

Punkty \(A,B,C,D\) należą do okręgu o środku \(O\). Jeśli kąt \(ABC\) ma miarę \(70^\circ \), to kąt \(DAC\) ma miarę: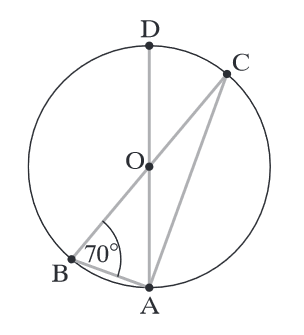

A.\( 70^\circ \)

B.\( 50^\circ \)

C.\( 40^\circ \)

D.\( 20^\circ \)

Trójkąty \(ABC\) i \(DEF\) są podobne. Obwód trójkąta \(ABC\) jest równy \(16\), a jego pole \(12\). Pole trójkąta \(DEF\) jest równe \(60\). Zatem obwód trójkąta \(DEF\) jest równy:

A.\( 80 \)

B.\( 16\sqrt{5} \)

C.\( \frac{16\sqrt{5}}{5} \)

D.\( \frac{16}{5} \)

Wykres funkcji \(f(x)=(4m-2)x+k-3\) przechodzi tylko przez II i IV ćwiartkę układu współrzędnych. Oznacza to, że:

A.\( \begin{cases} m\gt \frac{1}{2} \\ k=-3 \end{cases} \)

B.\( \begin{cases} m\lt \frac{1}{2} \\ k=-3 \end{cases} \)

C.\( \begin{cases} m\lt \frac{1}{2} \\ k=3 \end{cases} \)

D.\( \begin{cases} m\gt \frac{1}{2} \\ k=3 \end{cases} \)

Wzór funkcji, której wykres powstaje przez symetrię osiową względem osi \(OX\) wykresu funkcji \(f(x)=x^2-4\), to:

A.\( f(x)=(x+4)^2 \)

B.\( f(x)=-x^2-4\ \)

C.\( f(x)=-x^2+4\ \)

D.\( f(x)=(x-4)^2 \)

Wyrażenie wymierne \(W=\frac{x-3}{x^2-4x+4}\) jest określone dla

A.\( x\in \mathbb{R} \)

B.\( x\in \mathbb{R}\backslash \{3\} \)

C.\( x\in \mathbb{R}\backslash \{2\} \)

D.\( x\in \mathbb{R}\backslash \{-2,2\} \)

W trójkącie prostokątnym \(ABC\) przyprostokątne różnią się o \(4\), a jeden z kątów ma miarę \(30^\circ \). Krótsza przyprostokątna tego trójkąta ma długość:

A.\( \frac{2\sqrt{3}}{3} \)

B.\( \frac{2\sqrt{3}}{6} \)

C.\( 2\sqrt{3}-2 \)

D.\( 2\sqrt{3}+2 \)

Rozwiązaniem nierówności \((3x+9)^2\gt 0\) jest:

A.zbiór \( \mathbb{R} \)

B.zbiór pusty

C.zbiór \( \mathbb{R}\backslash \{-3\} \)

D.zbiór \( \mathbb{R}\backslash \{-9\} \)

Jeśli \(A=(-\infty,0)\) i \(B=\langle 0,5 \rangle \) to różnica przedziałów \(B\) i \(A\) jest równa:

A.\( (-\infty,0) \)

B.\( (-\infty,0\rangle \)

C.\( (0,5\rangle \)

D.\( \langle 0,5\rangle \)

\[B\backslash A=?\]

Dany jest trójkąt \(ABC\) o bokach długości \(4\) i \(6\) . Pole tego trójkąta jest równe \(3\sqrt{15}\). Oznacza to, że jeśli kąt między bokami o długościach \(4\) i \(6\) ma miarę \(\alpha \gt 90^\circ \), to:

A.\( \cos \alpha =\frac{\sqrt{15}}{4} \)

B.\( \cos \alpha =\frac{1}{4} \)

C.\( \cos \alpha =-\frac{\sqrt{15}}{4} \)

D.\( \cos \alpha =-\frac{1}{4} \)

Rzucono cztery razy monetą. Prawdopodobieństwo tego, że wypadnie co najwyżej \(1\) orzeł, jest równe:

A.\( \frac{2}{8} \)

B.\( \frac{5}{16} \)

C.\( \frac{4}{8} \)

D.\( \frac{4}{16} \)

Przekrój osiowy stożka jest trójkątem prostokątnym o przeciwprostokątnej długości \(12\). Pole powierzchni całkowitej stożka jest równe:

A.\( 6\pi (1+\sqrt{2}) \)

B.\( 36\pi (1+\sqrt{2}) \)

C.\( 24\pi \)

D.\( 36\pi \)

Suma \(n\) początkowych wyrazów ciągu arytmetycznego wyraża się wzorem \(S_n=3n^2+4n\). Piąty wyraz tego ciągu jest równy:

A.\( 45 \)

B.\( 31 \)

C.\( 21 \)

D.\( 11 \)

\[a_5=?\]

Funkcja \(f(x)=(m+3)x^2+16x+5\) osiąga wartość największą dla \(x=2\). Oznacza to, że największa wartość tej funkcji jest równa:

A.\( -7 \)

B.\( -14 \)

C.\( 14 \)

D.\( 21 \)

Sześcian \(ABCDA'B'C'D'\) przecięto płaszczyzną przechodzącą przez przekątną \(BD\) dolnej podstawy i wierzchołek \(C'\) górnej podstawy. Jeśli \(a\) jest krawędzią tego sześcianu, to pole otrzymanego przekroju jest równe:

A.\( \frac{1}{2}a^2\sqrt{2} \)

B.\( \frac{1}{2}a^2\sqrt{3} \)

C.\( \frac{1}{2}a^2\sqrt{5} \)

D.\( \frac{1}{2}a^2\sqrt{6} \)

Jeśli \(x+\frac{1}{x}=6\), to:

A.\( x^2+\frac{1}{x^2}=2\sqrt{6} \)

B.\( x^2+\frac{1}{x^2}=\sqrt{6} \)

C.\( x^2+\frac{1}{x^2}=36 \)

D.\( x^2+\frac{1}{x^2}=34 \)

Rozwiąż nierówność \((4x-1)^2\lt (2-5x)^2\).

\(x\epsilon \left(-\infty ,\frac{1}{3}\right)\cup (1,+\infty )\)

Narysuj wykres funkcji \(f(x)=2^x-3\). Podaj zbiór wartości tej funkcji.

\(ZW=(-3,+\infty )\)

Wykaż, że jeśli liczba rzeczywista \(a\) spełnia warunek \(a\lt 1\), to \(\frac{1}{1-a}\ge 4a\).

Wyznacz współczynniki \(b,c\) we wzorze funkcji \(f(x)=x^2+bx+c\), jeśli wiesz, że miejsca zerowe tej funkcji są równe \((-4)\) i \(2\). \[x_1 = -4\ x_2=2\ b=?\ c=?\]

\(b=2, c=-8\)

Wykaż, że jeśli liczby \((3^a,3^b,3^c)\) tworzą ciąg geometryczny, to liczby \((a,b,c)\) tworzą ciąg arytmetyczny.

Rzucono trzy razy sześcienną kostką do gry. Oblicz prawdopodobieństwo tego, że suma wyrzuconych oczek jest równa co najmniej \(16\).

\(\frac{5}{108}\)

Wyznacz długość boku kwadratu wpisanego w trójkąt równoboczny o boku \(a\) w ten sposób, że jeden bok kwadratu jest zawarty w boku trójkąta, a dwa wierzchołki kwadratu należą do pozostałych boków trójkąta.

\(a(2\sqrt{3}-3)\)

Dane są punkty \(A=(4,2)\) i \(B=(1,-3)\). Wyznacz współrzędne punktu \(C\) należącego do osi \(OY\), tak aby \(|\sphericalangle ACB|=90^\circ \).

\(C=(0,-2)\) lub \(C=(0,1)\)

Dany jest graniastosłup prawidłowy trójkątny o dolnej podstawie \(ABC\) i górnej \(A'B'C'\). Przekątna ściany bocznej tworzy z krawędzią podstawy kąt \(60^\circ \). Pole ściany bocznej graniastosłupa jest równe \(2\sqrt{3}\). Oblicz pole trójkąta \(ABC'\).

\(\frac{\sqrt{15}}{2}\)