Matura 2015 kwiecień PR

Drukuj

Poziom rozszerzony

Na tej stronie umieściłem kilka zadań treningowych do matury rozszerzonej.

Na rysunku przedstawiono fragment wykresu pochodnej funkcji \(f\)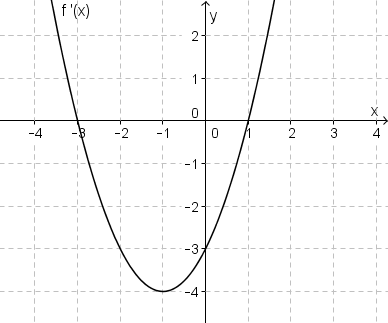

Minimum lokalne funkcja \(f\) osiąga w punkcie

A.\( x=-4 \)

B.\( x=-3 \)

C.\( x=-1 \)

D.\( x=1 \)

Leżeli \(\lim_{x \to \infty} \frac{(px+5)^3}{10x^3-5x^2+1}=-4\), to

A.\( p=-2\sqrt[3]{5} \)

B.\( p=-2\sqrt{10} \)

C.\( p=-\sqrt[3]{\frac{10}{4}} \)

D.\( p=-40 \)

Dana jest funkcja \(f(x)=\frac{x+1}{x-1}\). Rozwiąż równanie \(f'(x)=\frac{f(x)}{x}\).

\(x=-1-\sqrt{2}\) lub \(x=-1+\sqrt{2}\)

Funkcja \(f\) określona jest wzorem \(f(x)=x^3-4x\). Prosta o równaniu \(x=1\) przecina wykres funkcji \(f\) w punkcie \(P\). Znajdź równanie stycznej do wykresu funkcji \(f\) w punkcie \(P\).

\(y=-x-2\)

Wyznacz promień podstawy stożka o tworzącej długości \(5\), którego objętość jest największa.

\(r=\frac{5\sqrt{6}}{3}\)

Jednym z pierwiastków trójmianu kwadratowego \(y=ax^2+bx+c\) jest \(-\frac{1}{5}\). Liczby \(a\), \(b\), \(c\) tworzą ciąg arytmetyczny, a ich suma wynosi \(24\). Oblicz drugi pierwiastek tego trójmianu.

\(x=-\frac{1}{3}\)

Odcinek łączący środki dwóch skośnych krawędzi podstaw graniastosłupa prawidłowego czworokątnego ma długość \(10\). Jaką wysokość powinien mieć ten graniastosłup, aby pole jego powierzchni bocznej było maksymalne?

\(h=5\sqrt{2}\)