Granica funkcji w punkcie II

Drukuj

Poziom studiów

Definicja Cauchy'ego

Funkcja \(f(x)\) ma w punkcie \(x_0\) granicę \(g\), jeśli dla każdej liczby \(\epsilon \gt 0\) istnieje taka liczba \(\delta \gt 0\), że dla każdego \(x\) spełniającego: \(|x - x_0| \lt \delta\) zachodzi \(|f(x) - g| \lt \epsilon\).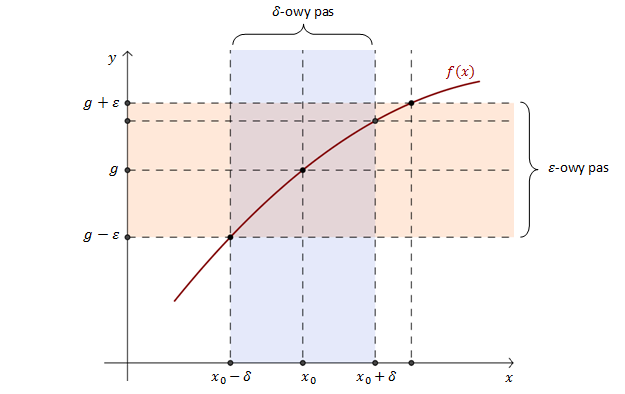

Ilustracja graficzna definicji Cauchy'ego granicy funkcji w punkcie.

Inne sformułowanie definicji Cauchy'ego:
Funkcja \(f(x)\) ma w punkcie \(x_0\) granicę \(g\), jeśli dla dowolnie małego pasa \(\epsilon\)-owego można znaleźć taki pas \(\delta\)-owy, że każdy punkt wykresu funkcji \(f(x)\) z pasa \(\delta\)-owego leży w pasie \(\epsilon\)-owym.

Zbadaj czy istnieje granica funkcji \(f(x)=e^{-\frac{1}{x}}\) w punkcie \(x_0=0\).

Granica nie istnieje - funkcja jest nieciągła.

Zbadaj czy istnieje granica funkcji \(f(x)=\frac{|x-1|}{x-1}-x\) w punkcie \(x_0=1\).

Granica nie istnieje - funkcja jest nieciągła.

Oblicz granice jednostronne funkcji \(f(x)=\frac{x}{x-2}\) w punkcie nienależącym do dziedziny.

\(\lim_{x \to 0^{-}}f(x)=-\infty \) i \(\lim_{x \to 0^{+}}f(x)=+\infty\)

Zbadaj czy istnieje Granica funkcji:

\(f(x)=x\sin \frac{1}{x}\) w punkcie \(x_0=0\)

\(f(x)=x\sin \frac{1}{x}-\cos \frac{1}{x}\) w punkcie \(x_0=0\)

a) istnieje i jest równa \(0\)
b) nie istnieje

Oblicz granicę: \(\lim_{x \to 1} \frac{1-\sqrt[3]{x}}{1-\sqrt[5]{x}}\).

\(\frac{5}{3}\)

Oblicz granicę \(\lim_{x \to 0} \frac{\cos px-\cos qx}{x^2}\), gdzie \(p,q\in \mathbb{R} \).

\(\frac{q^2-p^2}{2}\)