Grafy - definicje, własności, przykłady
Poziom studiów
Graf – to zbiór wierzchołków, które mogą być połączone krawędziami.
Przykładowy graf o \(6\) wierzchołkach i \(5\) krawędziach: 
Zbiór wierzchołków tego grafu to: \[V = \{1,2,3,4,5,6\}\] Zbiór krawędzi to: \[E = \{\{1,2\}, \{2,3\}, \{2,4\}, \{2,5\}, \{5,6\}\}\] Ten sam graf można też zilustrować graficznie np. w taki sposób: 
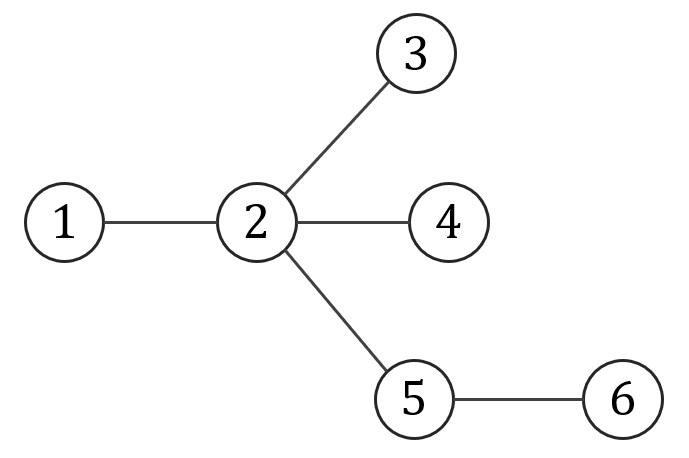Zbiór wierzchołków tego grafu to: \[V = \{1,2,3,4,5,6\}\] Zbiór krawędzi to: \[E = \{\{1,2\}, \{2,3\}, \{2,4\}, \{2,5\}, \{5,6\}\}\] Ten sam graf można też zilustrować graficznie np. w taki sposób: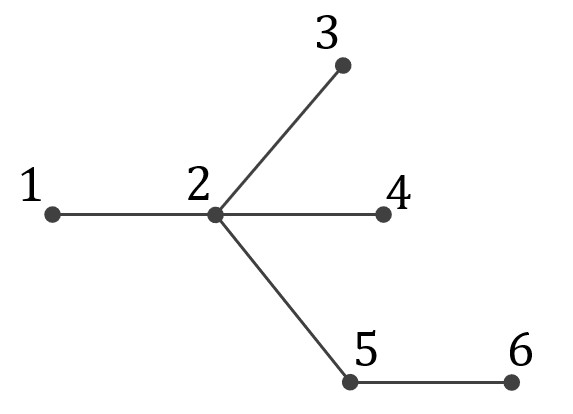 Definicja
Grafem nazywamy parę uporządkowaną \(G = (V, E)\), gdzie:- \(V\) – to niepusty zbiór wierzchołków.
- \(E\subset \bigl\{\{u,v\}: u,v\in V\bigr\}\) – to zbiór krawędzi, czyli dwuelementowych podzbiorów zbioru wierzchołków.
- Dla \(V = \{1,2,3\}\) i \(E = \{\{1,2\},\,\{2,3\}\}\) mamy graf o trzech wierzchołkach i dwóch krawędziach. Jedna krawędź łączy wierzchołek \(1\) z \(2\), a druga wierzchołek \(2\) z \(3\):
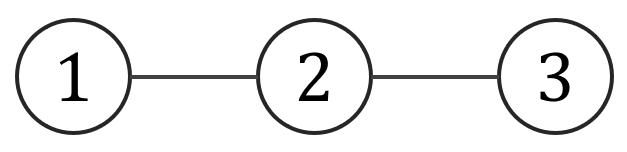
- Jeżeli \(V = \{a,b,c,d\}\) i \(E = \{\{a,b\},\,\{b,c\},\,\{c,d\},\,\{d,a\}\}\), to mamy graf o czterech wierzchołkach i czterech krawędziach:
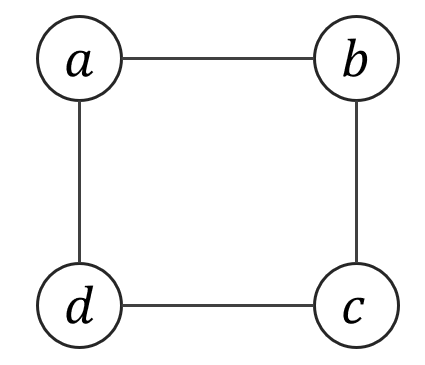
Definicja
Graf prosty – to taki graf, w którym nie ma pętli (krawędzi łączących wierzchołek z samym sobą) oraz nie ma krawędzi wielokrotnych (między tymi samymi parami wierzchołków jest najwyżej jedna krawędź).Definicja
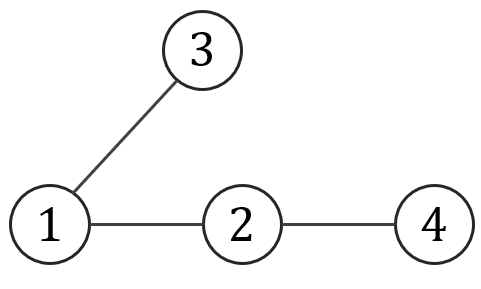
Stopień wierzchołka \(v\in V\) – to liczba krawędzi wychodzących z wierzchołka \(v\): \[ \deg(v)=\bigl|\{\,u\in V:\{v,u\}\in E\bigr\}\bigr|. \]- W grafie: \(V=\{1,2,3,4\}\), \(E=\{\{1,2\},\{1,3\},\{1,4\},\{2,3\}\}\) mamy: \[\deg(1)=3\] \[\deg(2)=2\] \[\deg(3)=2\] \[\deg(4)=1\]
Definicja
Macierz sąsiedztwa dla grafu o \(n\) wierzchołkach: \(V=\{v_1,v_2,\dots,v_n\}\) – to macierz kwadratowa \(n\times n\), w której:\(a_{ij} =\) liczba krawędzi między wierzchołkami \(v_i\) oraz \(v_j\).
Jeżeli graf jest nieskierowany, to macierz sąsiedztwa jest symetryczna.Jeżeli graf nie ma pętli, to na głównej przekątnej stoją zera.
Dla grafu \(G\) o wierzchołkach \(V=\{1,2,3,4\}\) i krawędziach \(E=\{\{1,2\},\{1,3\},\{2,4\}\}\): 
mamy macierz sąsiedztwa: \[ A(G)= \begin{pmatrix} 0 & 1 & 1 & 0\\ 1 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \end{pmatrix} \]
mamy macierz sąsiedztwa: \[ A(G)= \begin{pmatrix} 0 & 1 & 1 & 0\\ 1 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \end{pmatrix} \] Wyznaczyć graf \(G\) mający podaną poniżej macierz sąsiedztwa \[ M=\left(\begin{array}{lllll} 0 & 1 & 1 & 2 & 0 \\ 1 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 & 1 \\ 2 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 \end{array}\right) \]
Macierz jest wymiaru \(5\times 5\), czyli ma \(5\) wierzchołków. Z macierzy odczytujemy ile krawędzi łączy wierzchołek \(i\)-ty z \(j\)-tym. Przykładowo: \(a_{14}=2\), zatem między wierzchołkiem \(1\) i \(4\) są dwie krawędzie. 
Definicja
Graf pełny – to graf w którym każde dwa różne wierzchołki są połączone krawędzią.Graf pełny o \(n\) wierzchołkach oznaczamy \(K_n\), a liczba jego krawędzi to: \[\binom{n}{2} = \frac{n(n-1)}{2}\]
Definicja
Graf jest spójny jeżeli istnieje droga między każdymi dwoma wierzchołkami grafu.Definicja
Dopełnienie grafu \(G\) – to graf \({\overline {G}}\) w którym dwa wierzchołki są połączone krawędzią wtedy i tylko wtedy, gdy nie były połączone w grafie \(G\).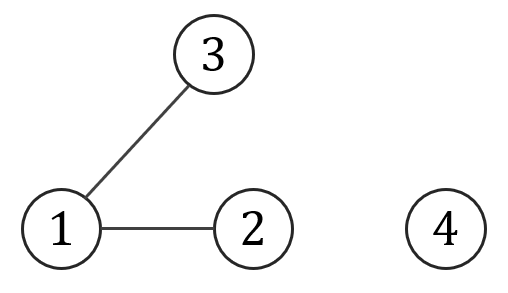 Oto przykład grafu \(G\), który nie jest spójny: 
Graf \(G\) nie jest spójny, ponieważ nie istnieje droga np. między wierzchołkiem \(1\) i \(4\).
Graf \(G\) nie jest spójny, ponieważ nie istnieje droga np. między wierzchołkiem \(1\) i \(4\). Dopełnienie \({\overline {G}}\) jest spójne i wygląda tak: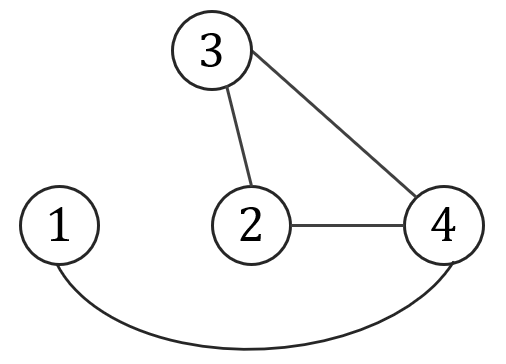 
Własności grafu pełnego \(K_n\)
- Stopień dowolnego wierzchołka wynosi \(n-1\).
- Macierz sąsiedztwa \(A(K_n)\) to macierz samych jedynek poza główną przekątną, gdzie są zera: \[ A(K_n)_{ij} = \begin{cases} 1, & i\neq j,\\ 0, & i=j. \end{cases} \]
- Graf \(K_n\) jest spójny.
- Dopełnienie grafu \(K_n\) jest grafem pustym (bez krawędzi) o \(n\) wierzchołkach.
\(K_4\) ma \(4\) wierzchołki i \(\binom{4}{2}=6\) krawędzi: 
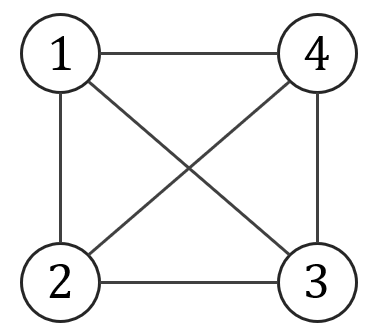Macierz sąsiedztwa: \[ A(K_4)= \begin{pmatrix} 0&1&1&1\\ 1&0&1&1\\ 1&1&0&1\\ 1&1&1&0 \end{pmatrix} \] Dopełnieniem grafu \(K_4\) jest graf pusty \({\overline {K_4}}\): 
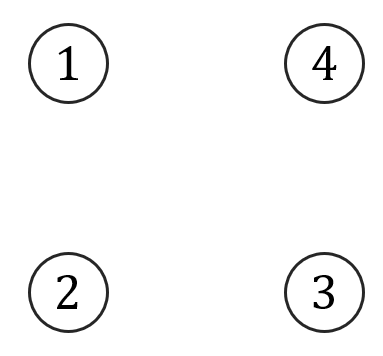Macierz sąsiedztwa: \[ A(\overline {K_4})= \begin{pmatrix} 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0 \end{pmatrix} \]
Macierz sąsiedztwa: \[ A(K_4)= \begin{pmatrix} 0&1&1&1\\ 1&0&1&1\\ 1&1&0&1\\ 1&1&1&0 \end{pmatrix} \] Dopełnieniem grafu \(K_4\) jest graf pusty \({\overline {K_4}}\): Macierz sąsiedztwa: \[ A(\overline {K_4})= \begin{pmatrix} 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0 \end{pmatrix} \] \(K_6\) ma \(6\) wierzchołków i \(\binom{6}{2}=15\) krawędzi: 
Macierz sąsiedztwa: \[ A(K_6)= \begin{pmatrix} 0&1&1&1&1&1\\ 1&0&1&1&1&1\\ 1&1&0&1&1&1\\ 1&1&1&0&1&1\\ 1&1&1&1&0&1\\ 1&1&1&1&1&0 \end{pmatrix} \] Dopełnieniem grafu \(K_6\) jest graf pusty \({\overline {K_6}}\) składający się z samych \(6\) wierzchołków, bez żadnej krawędzi.
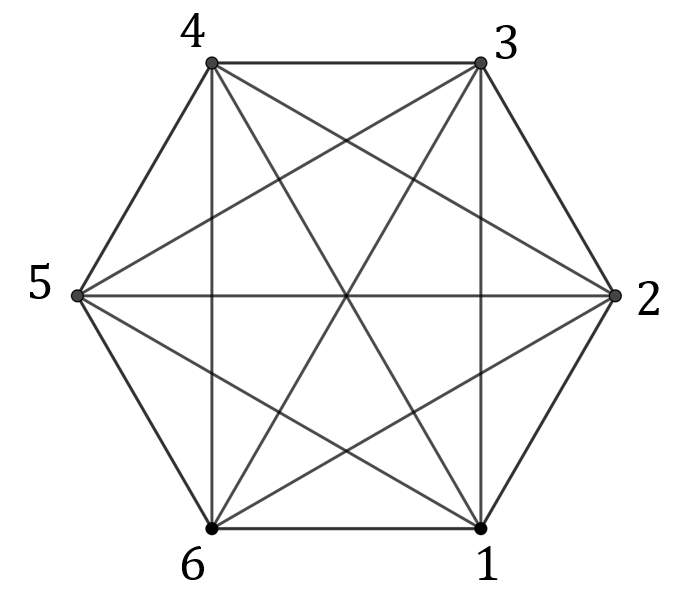Macierz sąsiedztwa: \[ A(K_6)= \begin{pmatrix} 0&1&1&1&1&1\\ 1&0&1&1&1&1\\ 1&1&0&1&1&1\\ 1&1&1&0&1&1\\ 1&1&1&1&0&1\\ 1&1&1&1&1&0 \end{pmatrix} \] Dopełnieniem grafu \(K_6\) jest graf pusty \({\overline {K_6}}\) składający się z samych \(6\) wierzchołków, bez żadnej krawędzi. Definicja
Graf dwudzielny \(K_{m,n}\) – to taki graf, którego wierzchołki dzielimy na dwie rozłączne zbiory: \[ X=\{x_1,x_2,\dots,x_m\},\quad Y=\{y_1,y_2,\dots,y_n\} \] i krawędzie mogą być tylko pomiędzy wierzchołkami z tych rozłącznych zbiorów. Nie ma krawędzi wewnątrz \(X\) ani wewnątrz \(Y\).Graf pełny dwudzielny \(K_{m,n}\) – to taki graf dwudzielny, w którym każdy wierzchołek z \(X\) jest połączony krawędzią z każdym wierzchołkiem z \(Y\). Wówczas liczba krawędzi takiego grafu wynosi: \[ \bigl|E(K_{m,n})\bigr| = m\cdot n. \]
Własności grafu pełnego \(K_{m,n}\)
- Stopień wierzchołka \(x_i\in X\) to \(n\), a stopień \(y_j\in Y\) to \(m\). Czyli: \[ \deg(x_i)=n,\quad \deg(y_j)=m. \]
- Graf jest spójny.
- Macierz sąsiedztwa w kolejności wierzchołków \((x_1,\dots,x_m,y_1,\dots,y_n)\) ma blokową postać: \[ A(K_{m,n}) = \begin{pmatrix} 0_{m\times m} & J_{m\times n}\\ J_{n\times m} & 0_{n\times n} \end{pmatrix}, \] gdzie \(0_{k\times k}\) to macierz zerowa stopnia \(k\), a \(J_{p\times q}\) to macierz samych jedynek wymiaru \(p\times q\).
- Dopełnieniem \(K_{m,n}\) jest suma grafu pełnego \(K_m\) o wierzchołkach \(X\) oraz grafu pełnego \(K_n\) o wierzchołkach \(Y\): \[\overline{K_{m,n}} = K_m \cup K_n\]
Graf pełny dwudzielny \(K_{2,4}\):
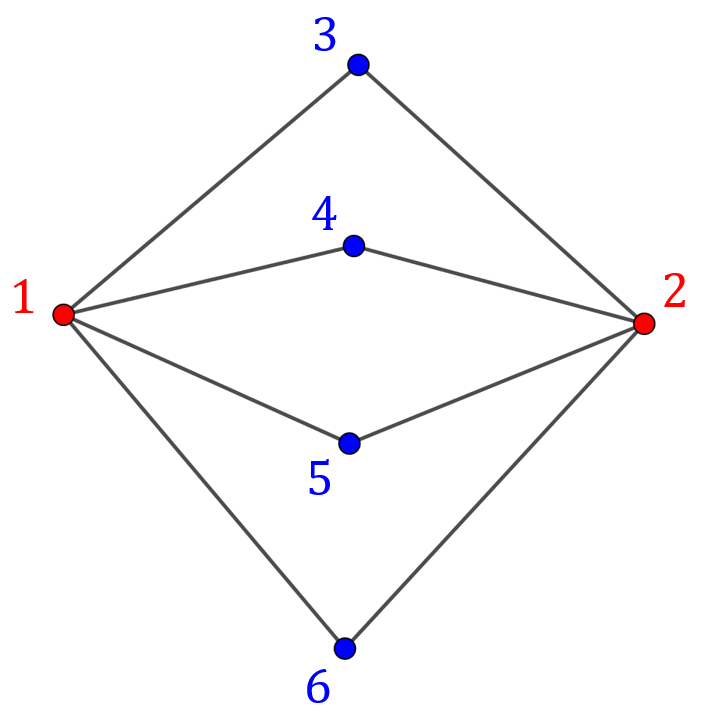
- \(X=\{1,2\},\;Y=\{3,4,5,6\}\).
- \(E=\{\{1,3\},\{1,4\},\{1,5\},\{1,6\},\{2,3\},\{2,4\},\{2,5\},\{2,6\}\}\)
- Macierz sąsiedztwa \(6\times6\) w kolejności \((1,2,3,4,5,6)\): \[ A(K_{2,4})= \begin{pmatrix} 0&0&1&1&1&1\\ 0&0&1&1&1&1\\ 1&1&0&0&0&0\\ 1&1&0&0&0&0\\ 1&1&0&0&0&0\\ 1&1&0&0&0&0 \end{pmatrix}. \]
- Ilustracja:
- Graf dopełniający \(\overline{K_{2,4}}\):
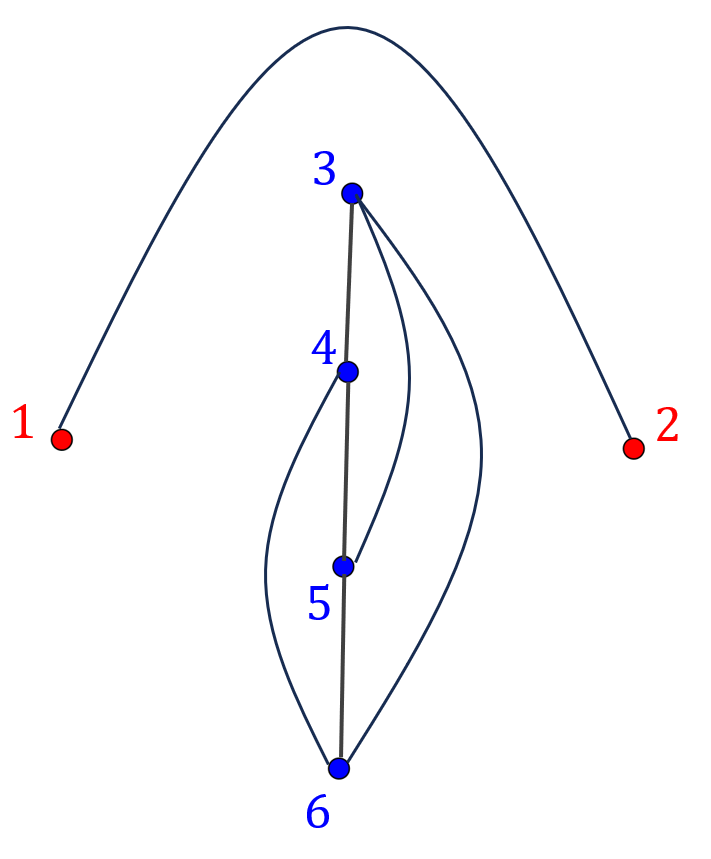Macierz sąsiedztwa grafu dopełniającego: \[ A\bigl(\overline{K_{2,4}}\bigr)= \begin{pmatrix} 0&1&0&0&0&0\\ 1&0&0&0&0&0\\ 0&0&0&1&1&1\\ 0&0&1&0&1&1\\ 0&0&1&1&0&1\\ 0&0&1&1&1&0 \end{pmatrix} \]
Graf pełny dwudzielny \(K_{1,7}\): 
- \(X=\{1\},\;Y=\{2,3,4,5,6,7,8\}\).
- \(E=\{\{1,2\},\{1,3\},\{1,4\},\{1,5\},\{1,6\},\{1,7\},\{1,8\}\}\).
- Macierz sąsiedztwa \(8\times8\) w kolejności \((1,2,3,4,5,6,7,8)\): \[ A(K_{1,7})= \begin{pmatrix} 0&1&1&1&1&1&1&1\\ 1&0&0&0&0&0&0&0\\ 1&0&0&0&0&0&0&0\\ 1&0&0&0&0&0&0&0\\ 1&0&0&0&0&0&0&0\\ 1&0&0&0&0&0&0&0\\ 1&0&0&0&0&0&0&0\\ 1&0&0&0&0&0&0&0 \end{pmatrix} \]
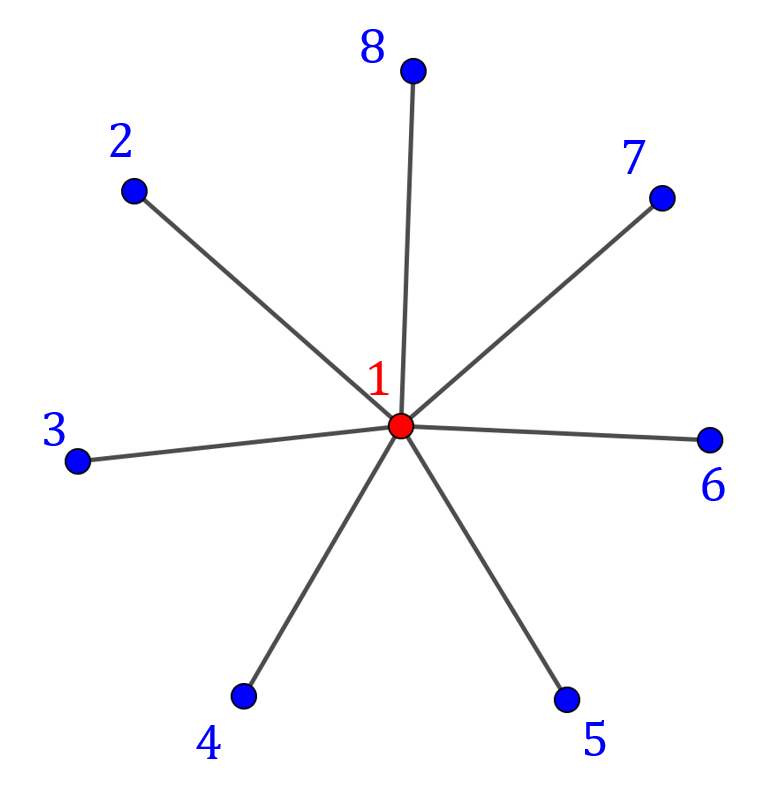
Definicja
Cykl \(C_n\) – to graf prosty o \(n\) wierzchołkach \(V=\{1,2,\dots,n\}\) i \(n\) krawędziach: \[ E = \bigl\{\{1,2\},\,\{2,3\},\,\dots,\,\{n-1,n\},\,\{n,1\}\bigr\}. \] Innymi słowy, wierzchołki są połączone kolejno i ostatni wraca do pierwszego.Własności cyklu \(C_n\)
- \(\bigl|E(C_n)\bigr| = n\), \(\bigl|V(C_n)\bigr| = n\).
- Stopień każdego wierzchołka jest równy \(2\) (czyli graf jest \(2\)-regularny).
- Graf jest spójny.
- Macierz sąsiedztwa w kolejności \((1,2,\dots,n)\): \[ A(C_n)_{i,j} = \begin{cases} 1, & \text{jeśli }j=i+1\text{ lub }j=i-1\\ 0, & \text{w przeciwnym razie}. \end{cases} \] Przykładowo dla \(n=6\): \[ A(C_6)= \begin{pmatrix} 0&1&0&0&0&1\\ 1&0&1&0&0&0\\ 0&1&0&1&0&0\\ 0&0&1&0&1&0\\ 0&0&0&1&0&1\\ 1&0&0&0&1&0 \end{pmatrix}. \]
Cykl \(C_6\):
- \(V=\{1,2,3,4,5,6\}\).
- \(E=\{\{1,2\},\{2,3\},\{3,4\},\{4,5\},\{5,6\},\{6,1\}\}\).
- Macierz sąsiedztwa \(6\times6\) w kolejności \((1,2,3,4,5,6)\): \[ A(C_6)= \begin{pmatrix} 0&1&0&0&0&1\\ 1&0&1&0&0&0\\ 0&1&0&1&0&0\\ 0&0&1&0&1&0\\ 0&0&0&1&0&1\\ 1&0&0&0&1&0 \end{pmatrix} \]
- Graf dla cyklu \(C_6\):
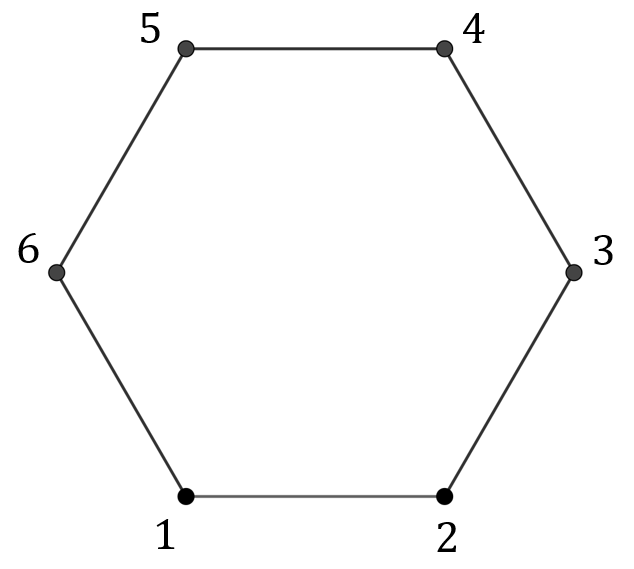
- Graf dopełniający \(\overline{C_6}\):
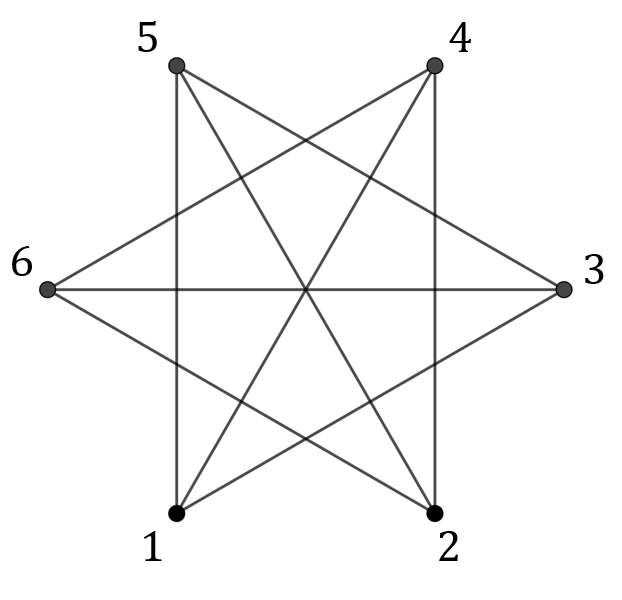Macierz sąsiedztwa grafu dopełniającego: \[ A\bigl(\overline{C_6}\bigr)= \begin{pmatrix} 0&0&1&1&1&0\\ 0&0&0&1&1&1\\ 1&0&0&0&1&1\\ 1&1&0&0&0&1\\ 1&1&1&0&0&0\\ 0&1&1&1&0&0 \end{pmatrix} \]
Definicja
Graf jest \(n\)-regularny jeżeli każdy jego wierzchołek jest stopnia \(n\).Definicja
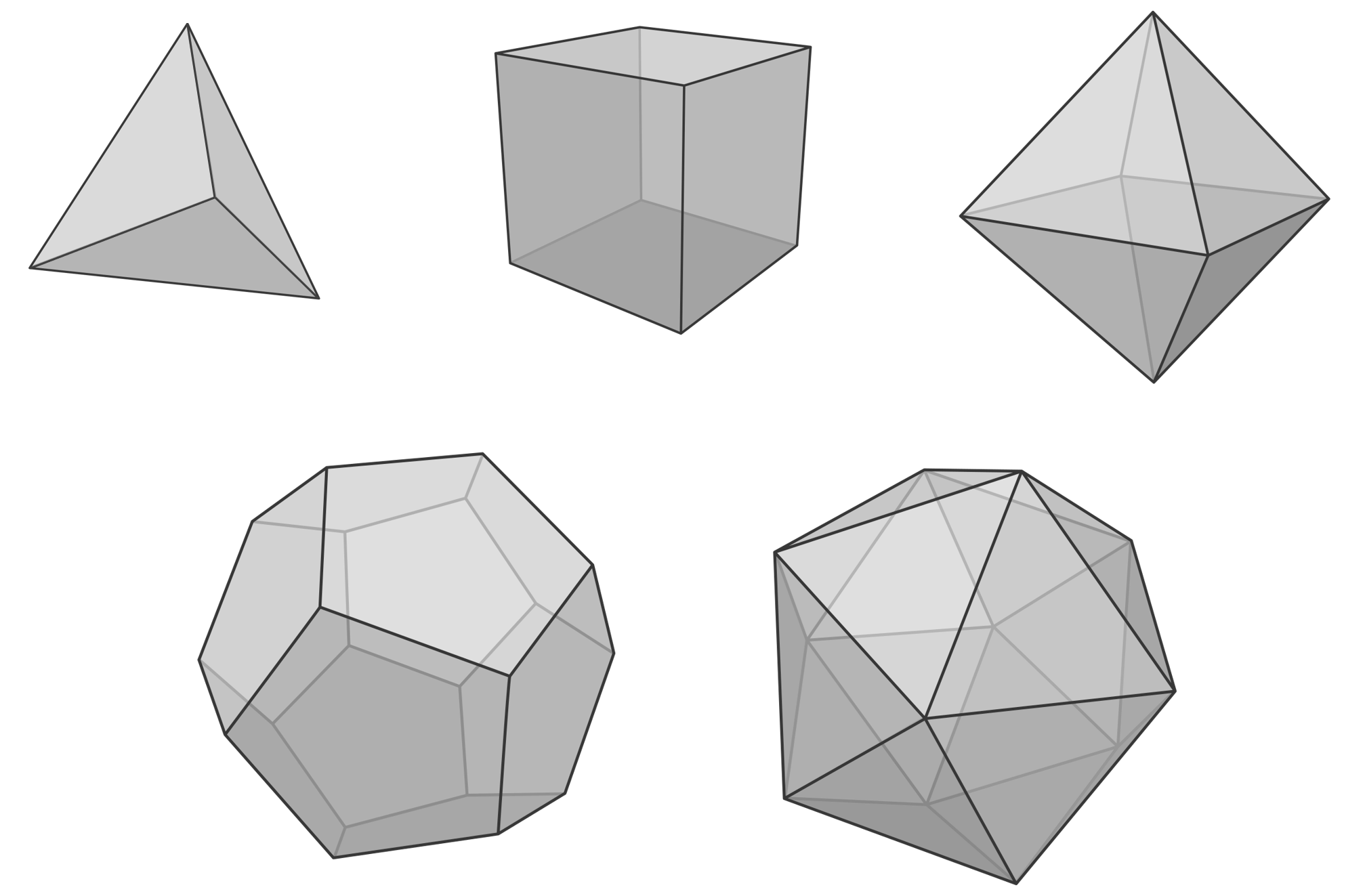
Graf platoński – to graf, utworzony z wierzchołków i krawędzi wielościanu foremnego. Istnieje dokładnie \(5\) wielościanów foremnych:- Czworościan foremny (graf \(K_4\)).
- Sześcian (graf o \(6\) wierzchołkach i \(12\) krawędziach, \(3\)-regularny).
- Ośmiościan foremny (graf o \(6\) wierzchołkach i \(12\) krawędziach, \(4\)-regularny).
- Dwunastościan foremny (graf o \(20\) wierzchołkach i \(30\) krawędziach, \(3\)-regularny).
- Dwudziestościan foremny (graf o \(12\) wierzchołkach i \(30\) krawędziach, \(5\)-regularny).
Izomorfizm grafów
Jeżeli dwa grafy mają taką samą liczbę wierzchołków i strukturę krawędzi między nimi, a różnią się jedynie położeniem wierzchołków, to powiemy, że są izomorficzne.Definicja
Dwa grafy \(G=(V,E)\) i \(G'=(V',E')\) nazywamy izomorficznymi, jeśli istnieje bijekcja (funkcja wzajemnie jednoznaczna) \(\varphi:V\to V'\) taka, że: \[ \{u,v\}\in E \;\Longleftrightarrow\; \{\varphi(u),\varphi(v)\}\in E'. \]Własności grafów izomorficznych
Grafy izomorficzne mają:- taką samą liczbę wierzchołków i krawędzi,
- odpowiednie wierzchołki mają te same stopnie.
Oto przykład dwóch grafów izomorficznych: 
Jeden graf powstał z drugiego przez przeniesienie jednego czerwonego wierzchołka na drugą stronę.
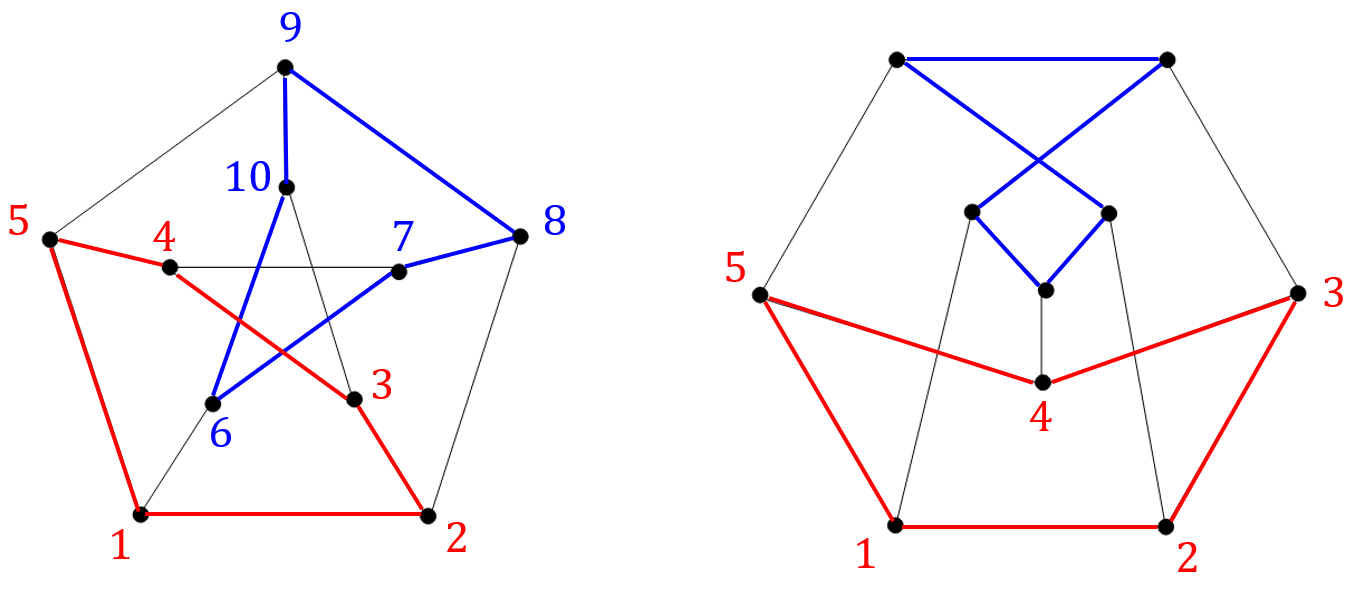
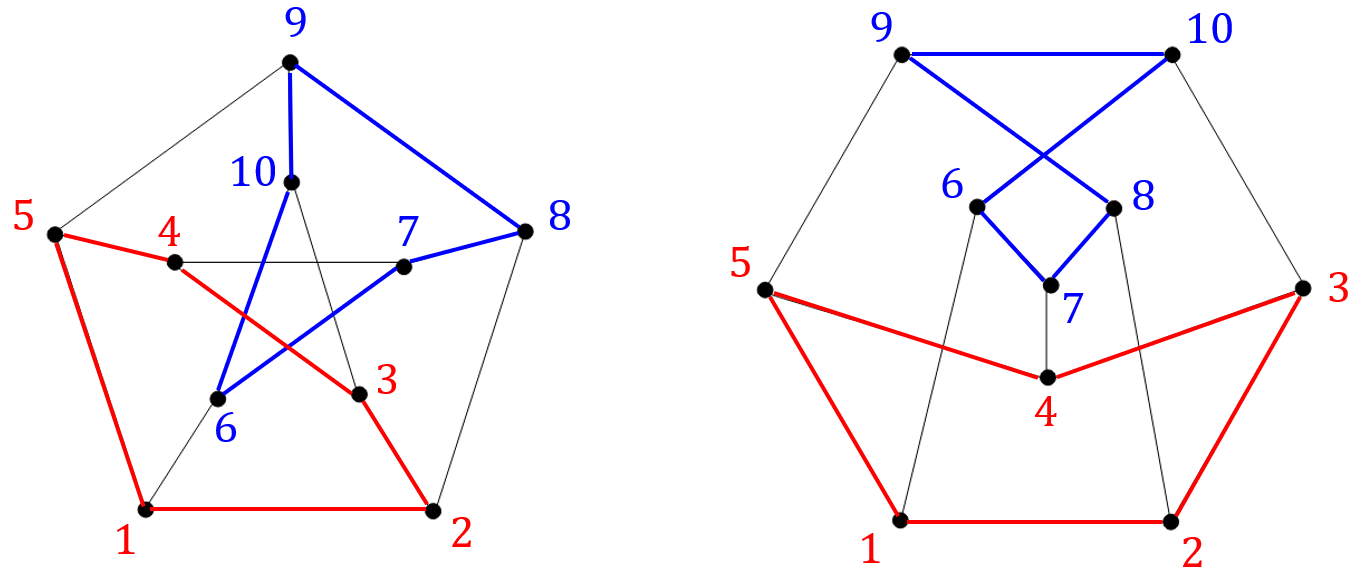
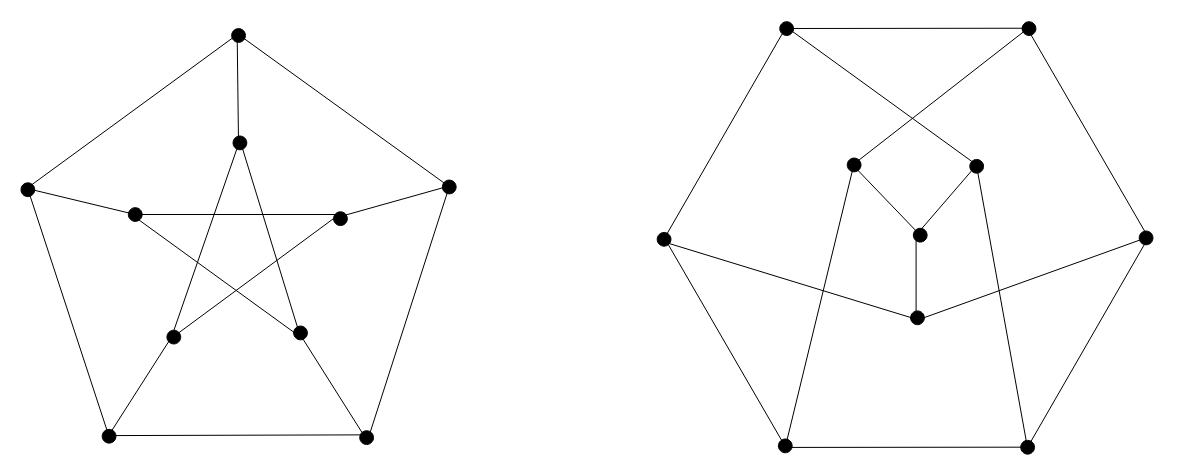
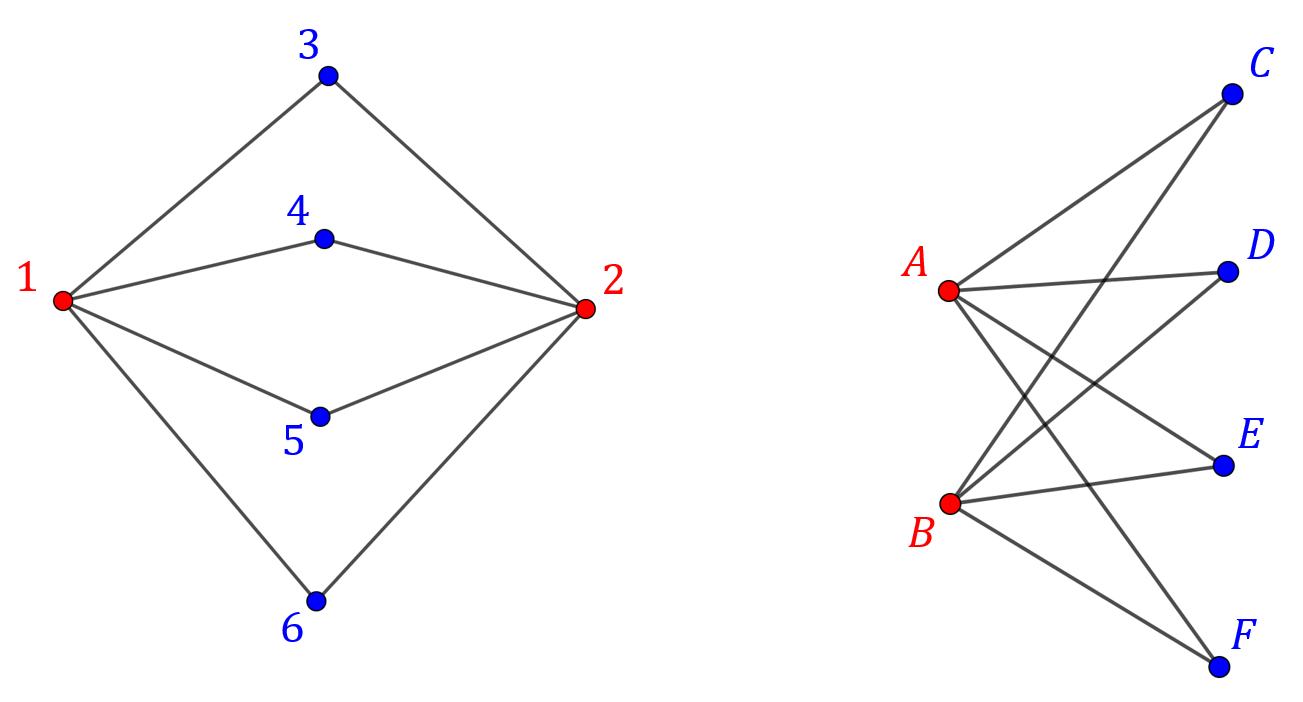Jeden graf powstał z drugiego przez przeniesienie jednego czerwonego wierzchołka na drugą stronę. Aby udowodnić, że grafy są izomorficzne, to należy zapisać formalnie bijekcję \(\varphi(v)\) przekształcającą jeden graf na drugi: \[\varphi(1)=A\] \[\varphi(2)=B\] \[\varphi(3)=C\] \[\varphi(4)=D\] \[\varphi(5)=E\] \[\varphi(6)=F\] Należy sprawdzić czy tak zdefiniowana bijekcja zachowuje krawędzie: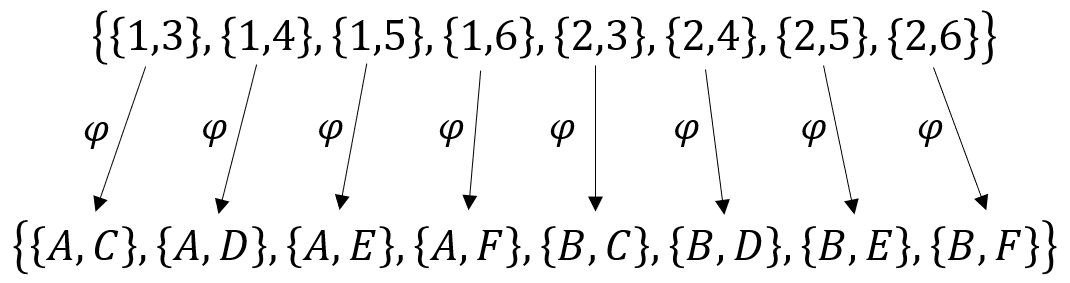 
Wszystkie krawędzie są przekształcone wzajemnie jednoznacznie, zatem grafy są izomorficzne.
Wykaż, że grafy:
- \(G_1\): \(V_1=\{1,2,3,4\}\), \(E_1=\{\{1,2\},\{1,3\},\{1,4\},\{2,3\}\}.\)
- \(G_2\): \(V_2=\{a,b,c,d\}\), \(E_2=\{\{a,b\},\{a,c\},\{a,d\},\{b,c\}\}.\)
Ustalmy bijekcję \(\varphi:V_1\to V_2\) następująco: \(\varphi(1)=a,\;\varphi(2)=b,\;\varphi(3)=c,\;\varphi(4)=d\).
Widać, że każda krawędź w \(G_1\) przechodzi na odpowiadającą krawędź w \(G_2\): \[\{1,2\}\xrightarrow{\varphi}\{a,b\}\] \[\{1,3\}\xrightarrow{\varphi}\{a,c\}\] \[\{1,4\}\xrightarrow{\varphi}\{a,d\}\] \[\{2,3\}\xrightarrow{\varphi}\{b,c\}\] Zatem grafy są izomorficzne.Definicja: Ścieżka i odległość
- Ścieżką w grafie \(G=(V,E)\) nazywamy ciąg kolejnych wierzchołków \((v_{i_0},v_{i_1},\dots,v_{i_k})\), taki że \(\{v_{i_j},v_{i_{j+1}}\}\in E\) dla \(j=0,1,\dots,k-1\).
- Długość ścieżki to liczba krawędzi, czyli \(k\).
- Graf jest spójny, jeśli dla każdej pary wierzchołków istnieje ścieżka między nimi.
- Odległością \(\mathrm{dist}(u,v)\) nazywamy najmniejszą długość ścieżki łączącej \(u\) z \(v\). Jeśli nie ma ścieżki, odległość jest nieskończona (lub ?brak połączenia?).
Dla grafu: odległość między \(1\) a \(6\) wynosi \(3\), bo ścieżka to \((1,2,5,6)\).
odległość między \(1\) a \(6\) wynosi \(3\), bo ścieżka to \((1,2,5,6)\). Definicja: Podgraf
Graf \(H=(W,F)\) jest podgrafem grafu \(G=(V,E)\), jeśli \(W\subset V\) i \(F\subset E\cap \bigl\{\{u,v\}:u,v\in W\bigr\}\). Jeżeli \(F = E\cap\bigl\{\{u,v\}:u,v\in W\bigr\}\), mówimy o podgrafie indukowanym przez \(W\).- W \(G=(\{1,2,3,4\},\{\{1,2\},\{2,3\},\{3,4\},\{1,4\}\})\) podgrafy indukowane przez \(\{1,2,3\}\) to \(H=(\{1,2,3\},\{\{1,2\},\{2,3\}\})\).
Definicja: Drzewo
Drzewem nazywamy spójny graf acykliczny (bez cykli). Alternatywnie graf prosty \(T=(V,E)\) jest drzewem wtedy i tylko wtedy, gdy liczba krawędzi \(|E| = |V| - 1\) i \(T\) jest spójny.Własności drzew
- Każdy wierzchołek o stopniu \(1\) to liść.
- Jeśli usuniemy dowolną krawędź z drzewa, graf się rozspójni (powstanie dwie składowe spójne).
- W drzewie istnieje dokładnie jedna ścieżka między dowolnymi dwoma wierzchołkami.
- Graf \(T=(\{1,2,3,4,5\},\{\{1,2\},\{1,3\},\{3,4\},\{3,5\}\})\) jest drzewem:
- Ma \(5\) wierzchołków i \(4\) krawędzie.
- Jest spójny i nie zawiera cykli.
Definicja: Spójność
Graf jest spójny, jeśli dla każdej pary wierzchołków \(u,v\in V\) istnieje ścieżka łącząca \(u\) z \(v\). Jeśli graf nie jest spójny, składa się z kilku składowych spójności.- Graf \(G=(\{1,2,3,4\},\{\{1,2\},\{3,4\}\})\) nie jest spójny ? ma dwie składowe: \(\{1,2\}\) i \(\{3,4\}\).
Definicja: Graf ważony i ścieżka najkrótsza
W grafie ważonym każda krawędź \(e\in E\) ma przypisaną wagę \(w(e)\in \mathbb{R}\). Wtedy długość ścieżki \((v_{i_0},v_{i_1},\dots,v_{i_k})\) obliczamy jako \[ \sum_{j=0}^{k-1} w\bigl(\{v_{i_j},v_{i_{j+1}}\}\bigr). \] Ścieżka najkrótsza to taka, która minimalizuje sumę wag.
- W grafie z wagami: \(V=\{1,2,3\}\), \(w(\{1,2\})=1,\;w(\{2,3\})=5,\;w(\{1,3\})=3\). Ścieżki z \(1\) do \(3\):
- \((1,3)\) o wadze \(3\).
- \((1,2,3)\) o wadze \(1+5=6\).
Definicja: Klika
Klika w grafie \(G=(V,E)\) to podgraf indukowany przez zbiór wierzchołków, który jest grafem pełnym. Mówiąc inaczej, zbiór \(U\subset V\) jest kliką, jeśli każda para wierzchołków w \(U\) jest połączona krawędzią.- W grafie \(G=(\{1,2,3,4\},\{\{1,2\},\{1,3\},\{2,3\},\{3,4\}\})\) klika to \(\{1,2,3\}\), ponieważ jest grafem \(K_3\). \(\{2,3,4\}\) nie jest kliką, bo brakuje krawędzi \(\{2,4\}\).
Definicja: Graf planarny
Graf \(G\) nazywamy planarnym, jeśli można go narysować na płaszczyźnie w taki sposób, że krawędzie się nie przecinają (poza wierzchołkami).Własności grafów planarnych
- Jeśli graf planarny \(G\) ma \(n\ge 3\) wierzchołków i \(m\) krawędzi, to: \[ m \le 3n - 6. \]
- W każdej takiej płaszczyznowej reprezentacji dziedzinę (obszary ograniczone krawędziami) nazywamy ścianami lub faces. Wzór Eulera: \(n - m + f = 2\), gdzie \(f\) to liczba ścian (wliczając ścianę zewnętrzną).
- Pełny graf \(K_5\) i pełny bipartytowy \(K_{3,3}\) nie są planarne (twierdzenie Kuratowskiego).
- Graf \(K_{3,3}\) to:
- \(X=\{1,2,3\},\;Y=\{4,5,6\}\).
- Krawędzie łączą każdą parę z \(X\) i \(Y\).\)
Definicja: Ścieżka Eulera i Ścieżka Hamiltona
- Ścieżka Eulera to ścieżka przechodząca dokładnie raz przez każdą krawędź grafu.
- Cykl Eulera to cykl (zwracający się do wierzchołka startowego), przechodzący każdą krawędź dokładnie raz.
- Ścieżka Hamiltona to ścieżka przechodząca przez każdy wierzchołek dokładnie raz.
- Cykl Hamiltona to cykl przechodzący przez wszystkie wierzchołki dokładnie raz.
Własności ścieżek Eulera
- Graf spójny ma cykl Eulera wtedy i tylko wtedy, gdy każdy wierzchołek ma parzysty stopień.
- Graf spójny ma ścieżkę Eulera (ale nie cykl) wtedy i tylko wtedy, gdy dokładnie dwa wierzchołki mają nieparzysty stopień, a pozostałe mają parzysty.
- Dla grafu \(G\) z \(V=\{1,2,3,4\}\), \(E=\{\{1,2\},\{2,3\},\{3,4\},\{4,1\}\}\) (cykl \(C_4\)) każdy wierzchołek ma stopień \(2\). Stąd istnieje cykl Eulera, np. \((1,2,3,4,1)\).
- Dla grafu \(G\) z \(V=\{1,2,3\}\), \(E=\{\{1,2\},\{2,3\}\}\): wierzchołki \(1,3\) mają stopień \(1\) (nieparzysty), wierzchołek \(2\) stopień \(2\). Istnieje ścieżka Eulera (ale nie cykl): \((1,2,3)\).
Definicja: Ścieżka Hamiltona ? przykład
Graf \(K_4\) (pełny graf na 4 wierzchołkach) ma cykl Hamiltona, np. \((1,2,3,4,1)\), oraz ścieżkę Hamiltona, np. \((1,3,2,4)\).
- Graf \(C_5\) (cykl pięciokąta) ma cykl Hamiltona (to sam cykl \(C_5\)) oraz ścieżki Hamiltona, np. \((1,2,3,4,5)\).
Definicja: Stopień minimalny i maksymalny
Dla grafu \(G=(V,E)\) definiujemy: \[ \delta(G) = \min_{v\in V} \deg(v), \quad \Delta(G) = \max_{v\in V} \deg(v). \]- W grafie \(G\) z \(V=\{1,2,3,4,5\}\), \(E=\{\{1,2\},\{2,3\},\{3,4\},\{4,5\}\}\): \(\deg(1)=\deg(5)=1,\;\deg(2)=\deg(3)=\deg(4)=2\). Stąd \(\delta(G)=1,\;\Delta(G)=2\).
Definicja: Graf skierowany (digraf)
Graf skierowany (digraf) to para \(D=(V,A)\), gdzie:- \(V\) to zbiór wierzchołków.
- \(A\subset V\times V\) to zbiór łuków (kierunkowych krawędzi) ? każdy łuk to uporządkowana para \((u,v)\).
- Digraf \(D\) z \(V=\{1,2,3\}\), \(A=\{(1,2),(2,3),(3,1)\}\) tworzy skierowany cykl o długości \(3\).
Definicja: Graf ważony nieskierowany
Graf ważony nieskierowany to \(G=(V,E,w)\), gdzie \(w:E\to\mathbb{R}\) przypisuje każdej krawędzi wagę. W dalszej części często pomijamy symbol \(w\), pisząc po prostu \(G=(V,E)\) i zakładając, że każda krawędź ma wagę \(1\) (graf nieważony) ? chyba że zaznaczymy inaczej.Definicja: Graf regularny
Graf nazywamy \(k\)-regularnym, jeśli każdy wierzchołek ma dokładnie stopień \(k\). Przykłady:- Graf \(K_n\) jest \((n-1)\)-regularny.
- Cykl \(C_n\) jest \(2\)-regularny.
- Sześciokąt foremny (cykl \(C_6\)) jest \(2\)-regularny.
- Graf siatki wierzchołków sześcianu jest \(3\)-regularny.
- Graf \(Q_3\) (sześcian) ? każdy wierzchołek połączony jest z trzema sąsiadami. Gdy oznaczymy wierzchołki binarnymi trójkami bitów \(\{000,001,010,011,100,101,110,111\}\), to krawędź istnieje, gdy kody różnią się jednym bitem. Jest to przykład grafu \(3\)-regularnego.
Definicja: Graf dwudzielny
Graf nazywamy dwudzielnym, jeśli jego wierzchołki da się podzielić na dwie rozłączne części \(X\) i \(Y\) (z \(V=X\cup Y\), \(X\cap Y=\emptyset\)), takie że każda krawędź łączy wierzchołek z \(X\) z wierzchołkiem z \(Y\). Nie ma krawędzi wewnątrz \(X\) ani wewnątrz \(Y\).Twierdzenie (charakterystyka grafów dwudzielnych)
Graf \(G\) jest dwudzielny wtedy i tylko wtedy, gdy nie zawiera cyklu nieparzystej długości (żaden podgraf indukowany nie jest cyklem nieparzystym).- Graf \(C_6\) jest dwudzielny (cykl parzysty), bo można podzielić wierzchołki na \(\{1,3,5\}\) i \(\{2,4,6\}\). Nie ma krawędzi wewnątrz tych zbiorów.
- Graf \(C_5\) nie jest dwudzielny, bo ma cykl nieparzysty.
Definicja: Graf składowe spójności
Składową spójności nazywamy podgraf \(H\subset G\), który jest maksymalnie spójny (nie można do niego dołączyć innego wierzchołka z \(G\) bez utraty spójności). Graf może składać się z kilku składowych spójności.- Dla \(G=(\{1,2,3,4,5\},\{\{1,2\},\{2,3\},\{4,5\}\})\) składowe to: \(\{1,2,3\}\) i \(\{4,5\}\).
Definicja: Minimum rozcinające (grafy ważone)
W grafie ważonym \(G=(V,E,w)\) cięcie (cut) to rozdzielenie \(V=X\cup Y\), \(X\cap Y=\emptyset\). Wartość cięcia to suma wag krawędzi łączących \(X\) z \(Y\). Minimum rozcinające to takie cięcie o minimalnej wartości.Ścieżka w grafie jest minimalna, gdy? [dowód odnośny do teorii minimalnych cięć ? skrócony]
- W grafie z wagami: \(V=\{A,B,C,D\}\), \(w(\{A,B\})=3,\;w(\{A,C\})=1,\;w(\{B,C\})=2,\;w(\{C,D\})=4,\;w(\{B,D\})=5\). Szukamy minimum rozcinającego między wierzchołkami \(\{A,B\}\) i \(\{C,D\}\). Można to zrobić metodami algorytmicznymi (Max-Flow / Min-Cut).
Definicja: Graf ewolucji (dynamiczny)
Graf ewolucji to graf, w którym w czasie następują zmiany ? dodawanie lub usuwanie wierzchołków i krawędzi. W modelach dynamicznych analizujemy, jak własności grafu zmieniają się w czasie.Inne ważne pojęcia
- Podgraf spójny ? spójny podgraf indukowany przez pewien zbiór wierzchołków.
- Ćwiczenia optymalizacyjne ? znajdowanie najkrótszej ścieżki (Dijkstra), najlżejszego drzewa rozpinającego (Kruskal, Prim), maksymalnego skojarzenia (Algorytm Hopcrofta?Karpa).
- Dualność grafów planarnych ? graf dualny do planarny, w którym wierzchołki odpowiadają ścianom, a krawędzie łączą ściany oddzielone daną krawędzią w grafie pierwotnym.
- Grafy regularne ? grafy \(k\)-regularne, np. \(C_n\), \(Q_d\) (graf hipersześcienny), grafy platoniczne.
- Grafy skończone vs nieskończone ? w opracowaniu omawiamy tylko grafy skończone.
- Graf skierowany vs nieskierowany.
- K-regularność ? każdy wierzchołek ma stopień \(k\).
- Graf komplementarny ? \(\overline{G}\) zawiera wszystkie krawędzie, które nie występują w \(G\).
- Graf ważony vs nieważony ? wagi na krawędziach vs domyślnie waga \(1\).
- Maksymalny stopień \(\Delta(G)\) i minimalny stopień \(\delta(G)\).
- Grafy Helly?ego, ramki ? (bardziej zaawansowane: koncepcje z teorii grafów turbidowych).
Powyższe pojęcia stanowią podstawę teorii grafów. W dalszych kursach można rozwijać temat: algorytmy grafowe (BFS, DFS, najkrótsza ścieżka, MST), grafy losowe, koloryzacja, przepływy w sieciach, spójność, 2-kolorowanie, twierdzenia o matroidach, co prowadzi do zaawansowanych zagadnień optymalizacyjnych.
Zestaw przykładowych zadań do samodzielnego rozwiązania:
-->- Zdefiniuj macierz sąsiedztwa dla grafu \(K_{3,3}\) i sprawdź, jakie jest \(\delta(G)\) i \(\Delta(G)\).
- Sprawdź, czy graf \(G=(\{1,2,3,4,5,6\},\{\{1,2\},\{2,3\},\{3,1\},\{4,5\},\{5,6\},\{6,4\},\{1,4\}\})\) jest spójny i znajdź wszystkie składowe, a także czy jest dwudzielny.
- Pokaż, że graf \(C_7\) nie jest dwudzielny i narysuj jego dopełnienie.
- Znajdź cykl Hamiltona w grafie sześcianu \(Q_3\), używając binarnego opisu wierzchołków.
Wykaż izomorfizm poniższych grafów: 
Wiedząc, że atom węgla \(C\) ma \(4\) wiązania, a atom wodoru \(H\) ma \(1\) wiązanie:
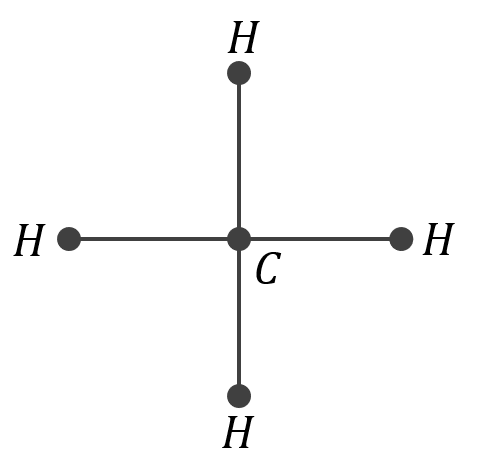
- Narysuj graf odpowiadający cząsteczce metanu \(CH_4\).
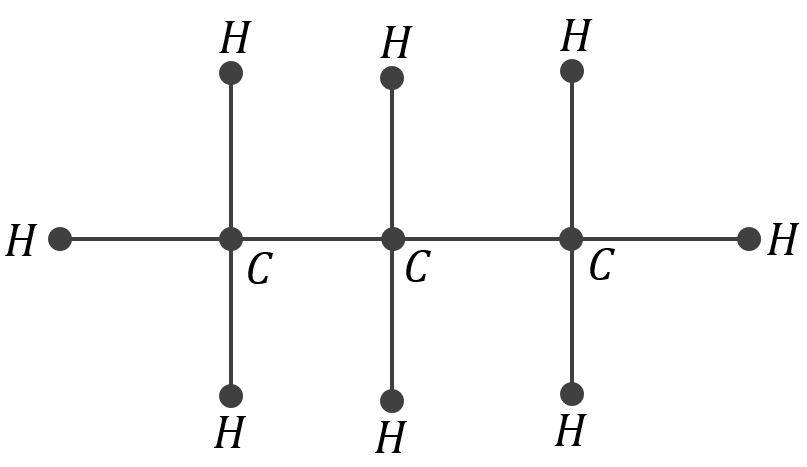
- Narysuj graf odpowiadający cząsteczce propanu \(C_3H_8\).
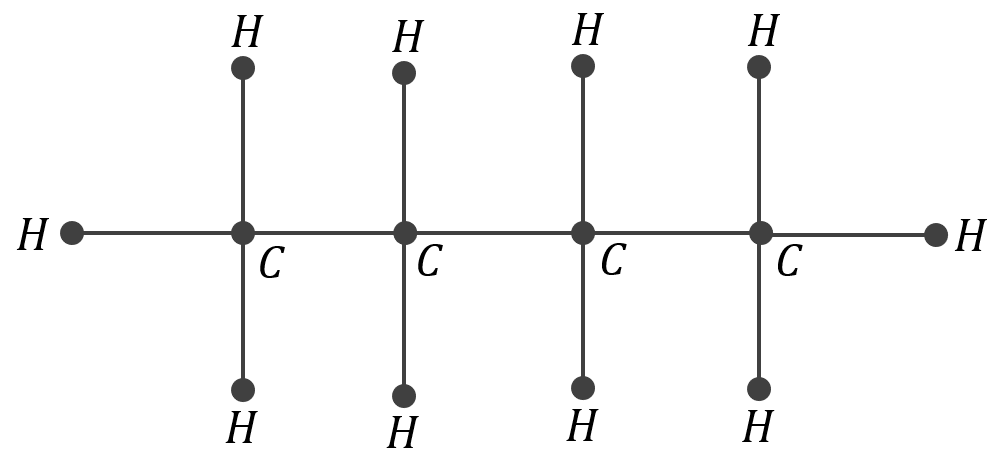
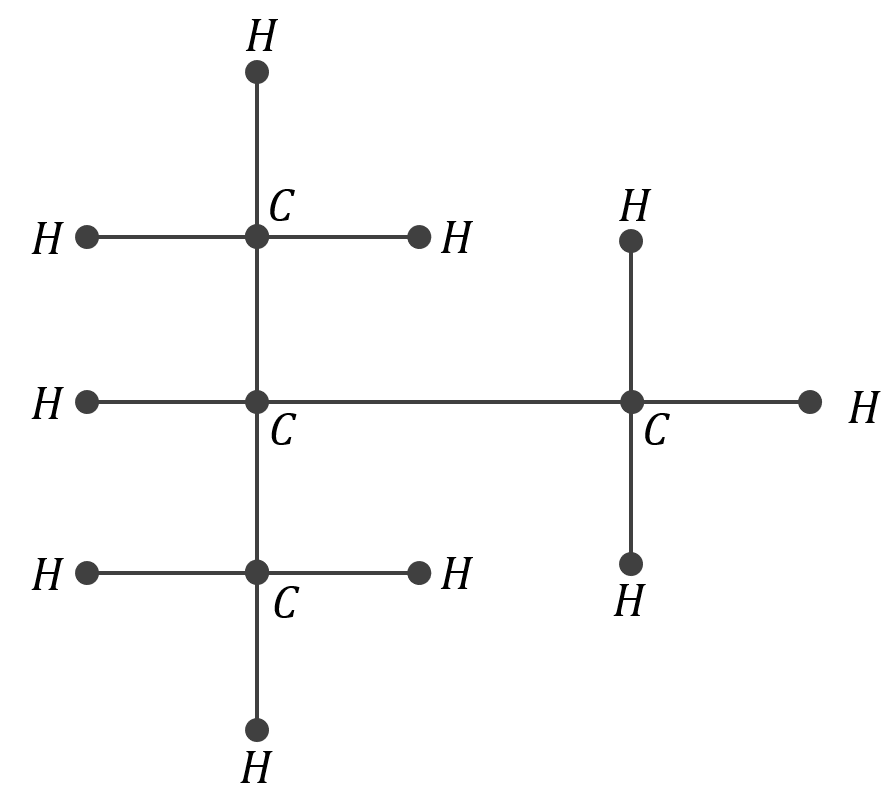
- Istnieją dwa różne węglowodory mające wzór sumaryczny \(C_4H_{10}\). Narysuj grafy odpowiadające ich cząstkom.
Narysuj wszystkie grafy proste nieoznakowane mające cztery wierzchołki.
Czy poniższe grafy są izomorficzne? Odpowiedź uzasadnij. 
Tematy nadrzędne i sąsiednie