Wykres proporcjonalności odwrotnej
Wykresem funkcji określonej wzorem \( f(x)=\frac{a}{x} \) jest hiperbola.
Narysuj wykres funkcji \(f(x)=\frac{1}{x}\).
Dziedzina tej funkcji to \(x\in \mathbb{R} \backslash \{0\}\).
Żeby narysować wykres wyznaczamy kilka punktów należących do tego wykresu:
Zatem: 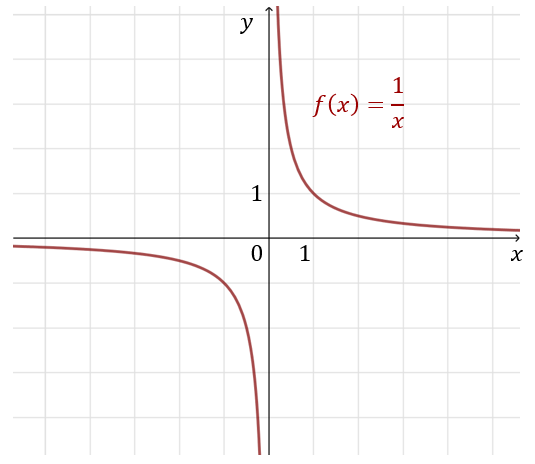
Żeby narysować wykres wyznaczamy kilka punktów należących do tego wykresu:
| \( x \) | \( -2 \) | \( -1 \) | \( -\frac{1}{4} \) | \( \frac{1}{2} \) | \( 1 \) | \( 2 \) | \( 3 \) |
| \( f(x)=\frac{1}{x} \) | \( -\frac{1}{2} \) | \( -1 \) | \( -4 \) | \( 2 \) | \( 1 \) | \( \frac{1}{2} \) | \( \frac{1}{3} \) |

Przykłady funkcji \( f(x)=\frac{a}{x} \) dla dodatnich współczynników \(a\). 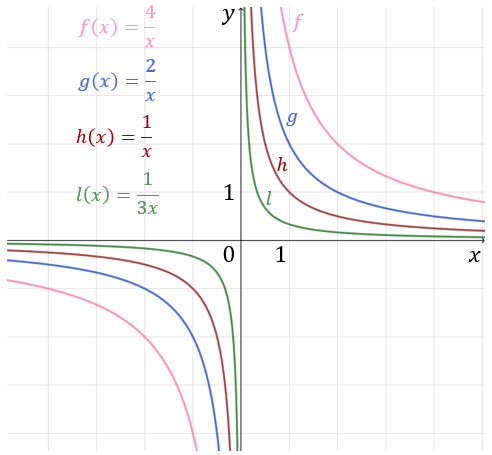 Własności funkcji o dodatnim współczynniku \(a\):
Własności funkcji o dodatnim współczynniku \(a\):
 Własności funkcji o dodatnim współczynniku \(a\):
Własności funkcji o dodatnim współczynniku \(a\): - Dziedzina: \(x\in \mathbb{R} \backslash \{0\}\).
- Brak miejsc zerowych.
- Funkcja jest malejąca w dwóch przedziałach \((-\infty ,0)\) oraz \((0, +\infty )\). Uwaga! Funkcja nie jest malejąca na całej swojej dziedzinie.
Wykres funkcji \( f(x)=\frac{a}{x} \) jest zawsze symetryczny względem początku układu współrzędnych.
Żeby narysować hiperbolę wystarczy narysować jedno ramię, a drugie będzie jej symetrycznym odbiciem.
Żeby narysować hiperbolę wystarczy narysować jedno ramię, a drugie będzie jej symetrycznym odbiciem.
Przykłady funkcji \( f(x)=\frac{a}{x} \) dla ujemnych współczynników \(a\). 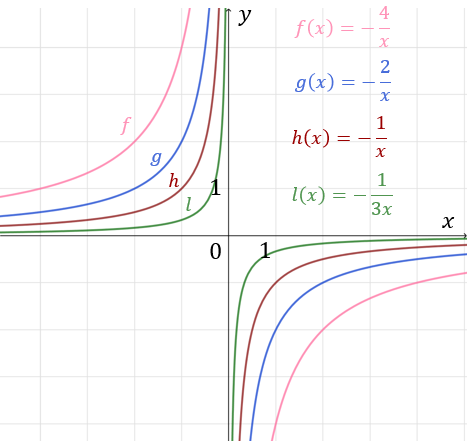 Własności funkcji o ujemnym współczynniku \(a\):
Własności funkcji o ujemnym współczynniku \(a\):
 Własności funkcji o ujemnym współczynniku \(a\):
Własności funkcji o ujemnym współczynniku \(a\): - Dziedzina: \(x\in \mathbb{R} \backslash \{0\}\).
- Brak miejsc zerowych.
- Funkcja jest rosnąca w dwóch przedziałach \((-\infty ,0)\) oraz \((0, +\infty )\). Uwaga! Funkcja nie jest rosnąca na całej swojej dziedzinie.
Ramiona wykresu funkcji \( f(x)=\frac{a}{x} \) zbliżają się do prostych \(y=0\) (oś \(x\)-ów) oraz \(x=0\) (oś \(y\)-ów). Takie proste nazywamy asymptotami wykresu funkcji - odpowiednio asymptotą poziomą i asymptotą pionową.
Samochód jadący z prędkością \(80 \frac{\text{km}}{\text{h}}\) pokonuje pewną drogę w \(3\) godziny. Wyznacz funkcję opisującą czas podróży w zależności od prędkości oraz naszkicuj jej wykres.
Wprowadźmy oznaczenia:
i rysujemy wykres: 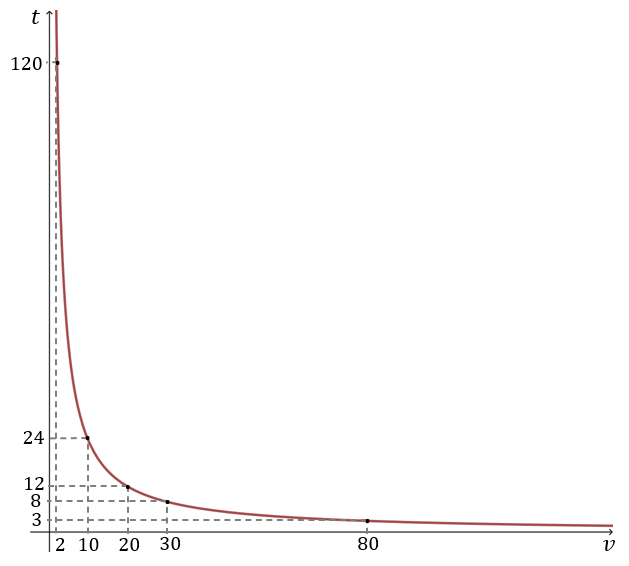 Z wykresu (oraz z tabelki) możemy odczytać, że:
Z wykresu (oraz z tabelki) możemy odczytać, że:
Można powiedzieć, że dziedziną funkcji \(t(v)=\frac{240}{v}\) jest \(v\in (0, +\infty )\) (dla uproszczenia pomijamy tutaj ograniczenia związane z prędkością światła i efekty z tym związane).
\( v \) - prędkość
\( t \) - czas
Długość drogi jest stała i możemy ją obliczyć mnożąc prędkość jazdy przez czas jazdy: \[80\cdot 3 = 240\ [\text{km}]\] Prędkość i czas są wielkościami odwrotnie proporcjonalnymi, zatem mamy: \[v\cdot t= 240\] Czyli: \[t=\frac{240}{v}\] Możemy powyższy wzór zapisać "bardziej profesjonalnie" w taki sposób: \[t(v)=\frac{240}{v}\] Dla tak otrzymanego wzoru funkcji wyznaczamy kilka punktów:\( t \) - czas
| \( v \) | \( 2 \) | \( 10 \) | \( 20 \) | \( 30 \) | \( 80 \) |
| \( t(v)=\frac{240}{v} \) | \( 120 \) | \( 24 \) | \( 12 \) | \( 8 \) | \( 3 \) |
 Z wykresu (oraz z tabelki) możemy odczytać, że:
Z wykresu (oraz z tabelki) możemy odczytać, że: - z prędkością \( 2 \frac{\text{km}}{\text{h}} \) motocyklista będzie jechał \( 120 \) godzin.
- z prędkością \( 10 \frac{\text{km}}{\text{h}} \) motocyklista będzie jechał \( 24 \) godziny.
- z prędkością \( 20 \frac{\text{km}}{\text{h}} \) motocyklista będzie jechał \( 12 \) godzin.
- z prędkością \( 30 \frac{\text{km}}{\text{h}} \) motocyklista będzie jechał \( 8 \) godzin.
Można powiedzieć, że dziedziną funkcji \(t(v)=\frac{240}{v}\) jest \(v\in (0, +\infty )\) (dla uproszczenia pomijamy tutaj ograniczenia związane z prędkością światła i efekty z tym związane).