Twierdzenie cosinusów
Twierdzenie cosinusów pozwala obliczyć długość boku trójkąta, w sytuacji gdy znamy długości dwóch pozostałych boków i kąt między nimi.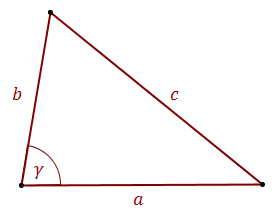 
Dla oznaczeń jak na powyższym rysunku zachodzi następujący wzór: \[c^2=a^2+b^2-2ab\cos \gamma \]
Dla oznaczeń jak na powyższym rysunku zachodzi następujący wzór: \[c^2=a^2+b^2-2ab\cos \gamma \] Warto zauważyć, że twierdzenie cosinusów, to jest uogólnione twierdzenie Pitagorasa.
Jeśli \(\gamma =90^\circ \), to mamy: \[ c^2=a^2+b^2-2ab\cos \gamma\\[6pt] c^2=a^2+b^2-2ab\cos 90^\circ \\[6pt] c^2=a^2+b^2-2ab\cdot 0\\[6pt] c^2=a^2+b^2 \]
Jeśli \(\gamma =90^\circ \), to mamy: \[ c^2=a^2+b^2-2ab\cos \gamma\\[6pt] c^2=a^2+b^2-2ab\cos 90^\circ \\[6pt] c^2=a^2+b^2-2ab\cdot 0\\[6pt] c^2=a^2+b^2 \]
W trójkącie \(ABC\) dane są długości dwóch boków \(|AB| = 12\), \(|BC| = 8\) oraz miara kąta \(|\sphericalangle ABC| = 60^\circ\).
Oblicz długość środkowej tego trójkąta, poprowadzonej z wierzchołka \(A\).
Dany jest trójkąt \(ABC\), w którym \(|AB| = 6\), \(|BC| = 5\), \(|AC| = 10\).
Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. | Cosinus kąta \(ABC\) jest równy \((−0{,}65)\). | P | F |
| Trójkąt \(ABC\) jest rozwartokątny. | P | F |