Środek odcinka
Środkiem odcinka \(AB\), gdzie \(A = (x_1, y_1)\) oraz \(B = (x_2, y_2)\) jest punkt: \[S=\left(\frac{x_1+x_2}{2}; \frac{y_1+y_2}{2}\right)\] 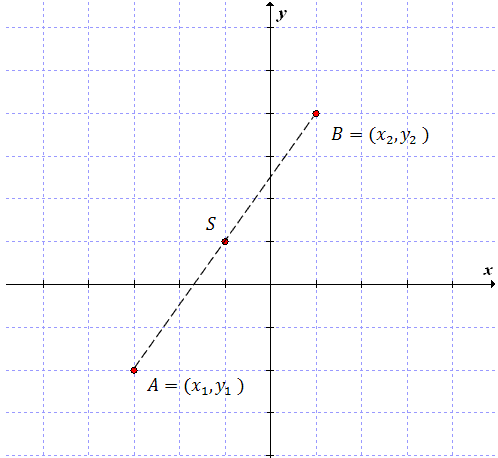

Punkt \(S=(-4, 7)\) jest środkiem odcinka \(PQ\), gdzie \(Q=(17, 12)\). Zatem punkt \(P\) ma współrzędne
A.\( P=(2, -25) \)
B.\( P=(38, 17) \)
C.\( P=(-25, 2) \)
D.\( P=(-12, 4) \)
Punkt \(S=(3,-1)\) jest środkiem odcinka \(AB\) i \(A=(-3,-5)\). Punkt \(B\) ma współrzędne:
A.\( (9,3) \)
B.\( (9,-3) \)
C.\( (-9,-3) \)
D.\( (-9,3) \)
Punkt \(S = (2, 7)\) jest środkiem odcinka \(AB\), w którym \(A = (-1, 3)\). Punkt \(B\) ma współrzędne:
A.\( B=(5,11) \)
B.\( B=\left (\frac{1}{2},2 \right) \)
C.\( B=\left (-\frac{3}{2},-5 \right) \)
D.\( B=(3,11) \)
Punkt \(S=(4,1)\) jest środkiem odcinka \(AB\), gdzie \(A=(a,0)\) i \(B=(a+3,\ 2)\). Zatem
A.\( a=0 \)
B.\( a=\frac{1}{2} \)
C.\( a=2 \)
D.\( a=\frac{5}{2} \)
Punkty \( A=(13,-12) \) i \( C=(15,8) \) są przeciwległymi wierzchołkami kwadratu \( ABCD \). Przekątne tego kwadratu przecinają się w punkcie
A.\(S=(2,-20) \)
B.\(S=(14,10) \)
C.\(S=(14,-2) \)
D.\(S=(28,-4) \)
Dane są punkty \(M=(-2,1)\) i \(N=(-1,3)\). Punkt \(K\) jest środkiem odcinka \(MN\). Obrazem punktu \(K\) w symetrii względem początku układu współrzędnych jest punkt
A.\( K'=\left ( 2,-\frac{3}{2} \right ) \)
B.\( K'=\left ( 2,\frac{3}{2} \right ) \)
C.\( K'=\left ( \frac{3}{2},2 \right ) \)
D.\( K'=\left ( \frac{3}{2},-2 \right ) \)
Punkt \(K=(-4,4)\) jest końcem odcinka \(KL\), punkt \(L\) leży na osi \(Ox\), a środek \(S\) tego odcinka leży na osi \(Oy\). Wynika stąd, że
A.\( S=(0,2) \)
B.\( S=(-2,0) \)
C.\( S=(4,0) \)
D.\( S=(0,4) \)
Punkt \(S = (2,−5)\) jest środkiem odcinka \(AB\), gdzie \(A = (−4,3)\) i \(B = (8,b)\). Wtedy
A.\( b=-13 \)
B.\( b=-2 \)
C.\( b=-1 \)
D.\( b=6 \)
W układzie współrzędnych na płaszczyźnie dany jest odcinek \(AB\) o końcach w punktach \(A=(7,4)\), \(B=(11,12)\). Punkt \(S\) leży wewnątrz odcinka \(AB\) oraz \(|AS|=3\cdot |BS|\). Wówczas
A.\( S=(8,6) \)
B.\( S=(9,8) \)
C.\( S=(10,10) \)
D.\( S=(13,16) \)