Różne zadania z trójkątów

W trójkącie prostokątnym dwa dłuższe boki mają długości \(\sqrt{5}\) i \(3\). Obwód tego trójkąta jest równy

A.\( 5+\sqrt{5} \)

B.\( 5\sqrt{5} \)

C.\( 5+2\sqrt{5} \)

D.\( \sqrt{30} \)

W trójkącie równoramiennym \( ABC \) dane są \( |AC|=|BC|=5 \) oraz wysokość \( |CD|=2 \). Podstawa \( AB \) tego trójkąta ma długość

A.\(6 \)

B.\(2\sqrt{21} \)

C.\(2\sqrt{29} \)

D.\(14 \)

W trójkącie prostokątnym dwa dłuższe boki mają długości \(5\) i \(7\). Obwód tego trójkąta jest równy

A.\(16\sqrt{6} \)

B.\(14\sqrt{6} \)

C.\(12+4\sqrt{6} \)

D.\(12+2\sqrt{6} \)

Oblicz pole trójkąta równoramiennego \(ABC\), w którym \(|AB| = 24\) i \(|AC| = |BC| = 13\).

\(60\)

Liczby \(4, 10, c\) są długościami boków trójkąta równoramiennego. Oblicz \(c\).

\(c=10\)

Liczby \(6, 10, c\) są długościami boków trójkąta równoramiennego. Oblicz \(c\).

\(c=6\) lub \(c=10\)

Liczby \(6, 10, c\) są długościami boków trójkąta prostokątnego. Oblicz \(c\).

\(c=2\sqrt{34}\) lub \(c=8\)

Liczby \(x - 1, x, 5\) są długościami boków trójkąta równoramiennego. Oblicz \(x\).

\(x=5\) lub \(x=6\)

Punkt \(S\) jest środkiem wysokości \(CD\) trójkąta równoramiennego \(ABC\), w którym \(|AC|=|BC|=5\) oraz \(|CD|=4\) (zobacz rysunek).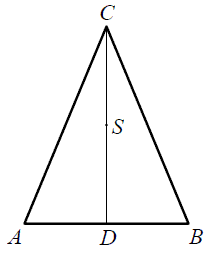

Odległość punktu \(S\) od ramienia tego trójkąta jest równa

A.\( \frac{6}{5} \)

B.\( \frac{3}{2} \)

C.\( \frac{12}{5} \)

D.\( \frac{5}{2} \)

W trójkącie równoramiennym \(ABC\) o wysokościach \(CD\) i \(AE\) podstawa \(AB\) ma długość \(8\) cm, a odcinek \(BE\) ma długość \(3\) cm.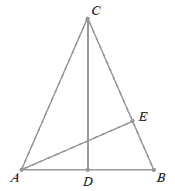

Długość odcinka \(AC\) jest równa:

A.\( 6 \) cm

B.\( \frac{32}{3} \) cm

C.\( \frac{28}{3} \) cm

D.\( \frac{33}{2} \) cm

Długość odcinka \(BD\) w trójkącie prostokątnym \(ABC\) jest równa: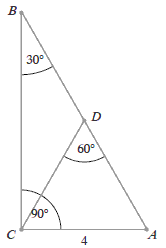

A.\( \frac{9\sqrt{3}}{4} \)

B.\( 4 \)

C.\( 4\sqrt{3} \)

D.\( 4\sqrt{2} \)

Dany jest trójkąt \(ABC\), gdzie \(A=(-3,-2)\), \(B=(1,-1)\), \(C=(-1,4)\). Wyznacz równanie symetralnej boku \(AC\) tego trójkąta.

\(y=-\frac{1}{3}x+\frac{1}{3}\)

Dany jest trójkąt równoramienny, w którym ramię o długości \( 20 \) tworzy z podstawą kąt \( 67{,}5^\circ \). Pole tego trójkąta jest równe

A.\( 100\sqrt{3} \)

B.\( 100\sqrt{2} \)

C.\( 200\sqrt{3} \)

D.\( 200\sqrt{2} \)

Punkty \( A=(3,3) \text{ i } B=(9,1) \) są wierzchołkami trójkąta \( ABC \), a punkt \( M=(1,6) \) jest środkiem boku \( AC \). Oblicz współrzędne punktu przecięcia prostej \( AB \) z wysokością tego trójkąta, poprowadzoną z wierzchołka \( C \).

\((-2{,}4;\ 4{,}8)\)

Na trójkącie o bokach długości \(\sqrt{7}, \sqrt{8}, \sqrt{15}\) opisano okrąg. Oblicz promień tego okręgu.

\(r=\frac{\sqrt{15}}{2}\)

Długości przyprostokątnych trójkąta prostokątnego są równe \(4\) i \(6\). Środkowa tego trójkąta poprowadzona z wierzchołka kąta prostego ma długość

A.\( \sqrt{13} \)

B.\( \sqrt{52} \)

C.\( 5 \)

D.\( 2 \)

W trójkącie równoramiennym \(ABC\) spełnione są warunki: \(|AC|=|BC|\), \(|\sphericalangle CAB|=50^\circ \). Odcinek \(BD\) jest dwusieczną kąta \(ABC\), a odcinek \(BE\) jest wysokością opuszczoną z wierzchołka \(B\) na bok \(AC\). Miara kąta \(EBD\) jest równa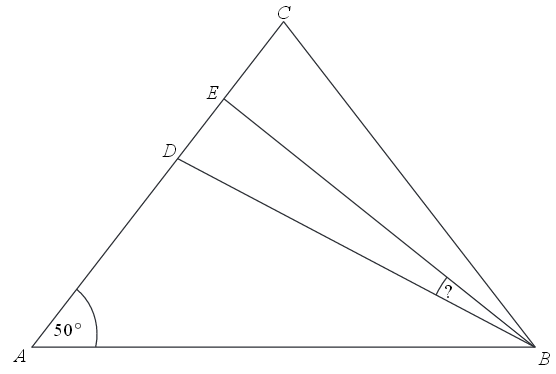

A.\( 10^\circ \)

B.\( 12{,}5^\circ \)

C.\( 13{,}5^\circ \)

D.\( 15^\circ \)

Wyznacz równanie osi symetrii trójkąta o wierzchołkach \(A = (−2, 2)\), \(B = (6, − 2)\), \(C = (10,6)\).

\(y=-3x+16\)