Rozkład wielomianu na czynniki
Rozłożenie wielomianu na czynniki, polega na zapisaniu jego wzoru w postaci iloczynu nawiasów.
Taki sposób zapisu wielomianu nazywamy postacią iloczynową.
Taki sposób zapisu wielomianu nazywamy postacią iloczynową.
| Postać ogólna | Postać iloczynowa |
| \(W(x) = x^2 - 4\) | \(W(x) = (x - 2)(x + 2)\) |
| \(W(x) = x^2 - 25\) | \(W(x) = (x - 5)(x + 5)\) |
| \(W(x) = x^2 - 6x + 9\) | \(W(x) = (x - 3)^2\) |
| \(W(x) = x^2 + 5x + 6\) | \(W(x) = (x + 2)(x + 3)\) |
| \(W(x) = x^2 + x - 30\) | \(W(x) = (x - 5)(x + 6)\) |
| \(W(x) = x^3 + x^2 - 4x - 4\) | \(W(x) = (x - 2)(x + 2)(x + 1)\) |
| \(W(x) = x^3 - 2x^2 - 9x + 18\) | \(W(x) = (x - 2)(x + 3)(x - 3)\) |
| \(W(x) = 3x^3 + 4x^2 - 147x - 196\) | \(W(x) = (x - 7)(x + 7)(3x + 4)\) |
| \(W(x) = x^3 + 4x^2 - 7x - 10\) | \(W(x) = (x - 2)(x + 1)(x + 5)\) |
| \(W(x) = x^3 - 8\) | \(W(x) = (x - 2)(x^2 + 2x + 4)\) |
| \(W(x) = x^3 + 5x\) | \(W(x) = x(x^2 + 5)\) |
| \(W(x) = x^4 - 16\) | \(W(x) = (x - 2)(x + 2)(x^2 + 4)\) |
| \(W(x) = x^4 + 4x^3 + x^2 - 8x - 6\) | \(W(x) = (x - \sqrt{2})(x + \sqrt{2})(x + 1)(x + 3)\) |
| \(W(x) = x^2 + 1\) | nie istnieje |
| \(W(x) = x^2 - x + 5\) | nie istnieje |
Jeżeli dany jest wielomian w postaci iloczynowej, to zawsze można przekształcić go do postaci ogólnej. Wystarczy wymnożyć nawiasy wyraz za wyrazem (tak jak mnożymy wyrażenia algebraiczne).
Zapisz wielomian \(W(x) = (x - 2)(x + 1)\) w postaci ogólnej.
Wymnażamy nawiasy: \[W(x) = (x - 2)(x + 1) = x^2 + x - 2x - 2 = x^2 - x - 2\] Czyli: \[W(x) = x^2 - x - 2\]
Łatwo można przekształcić wielomian z postaci iloczynowej na postać ogólną. Trudniej jest wykonać przekształcenie w drugą stronę.
Zapisz wielomian \(W(x) = x^2 - 4\) w postaci iloczynowej.
Do rozkładania wielomianów na iloczyn czynników najczęściej stosujemy takie metody jak: Wykorzystamy wzór skróconego mnożenia: \[a^2-b^2=(a-b)(a+b)\] Możemy zapisać, że: \[W(x) = x^2 - 4 = (x - 2)(x + 2)\] Zatem szukana postać iloczynowa, to: \[W(x) = (x - 2)(x + 2)\]
- wyciąganie wspólnego czynnika przed nawias,
- wzory skróconego mnożenia,
- deltę (\(\Delta \)),
- grupowanie wyrazów.
Metoda wyciągania wspólnego czynnika przed nawias
Przed nawias możemy wyciągać zarówno liczbę jak i literkę, która występuje w każdym z jednomianów tworzących wielomian.
Rozkładając wielomian na czynniki zawsze zaczynamy od sprawdzenia, czy nie da się wyciągnąć wspólnego czynnika przed nawias ze wszystkich jednomianów.
Metoda wyciągania wspólnego czynnika przed nawias została zilustrowana na poniższych przykładach. Rozłóż wielomian \(W(x) = x^2 - 7x\) na czynniki.
Wspólnym czynnikiem każdego z dwóch jednomianów tworzących ten wielomian jest \(x\).
Wyciągamy go przed nawias: \[W(x) = x^2 - 7x = x(x - 7)\]
Wyciągamy go przed nawias: \[W(x) = x^2 - 7x = x(x - 7)\]
Rozłóż wielomian \(W(x) = 7x^3 + 21x\) na czynniki.
Wspólnym czynnikiem każdego z dwóch jednomianów tworzących ten wielomian jest \(7x\).
Wyciągamy go przed nawias: \[W(x) = 7x^3 + 21x = 7x(x^2 + 3)\]
Wyciągamy go przed nawias: \[W(x) = 7x^3 + 21x = 7x(x^2 + 3)\]
Rozłóż wielomian \(W(x) = 4x^3 + 6x^2\) na czynniki.
Wspólnym czynnikiem każdego z dwóch jednomianów tworzących ten wielomian jest \(2x^2\).
Wyciągamy go przed nawias: \[W(x) = 4x^3 + 6x^2 = 2x^2(2x + 3)\] Uwaga! Jeżeli chcemy upewnić się, że dobrze wyciągnęliśmy wspólny czynnik przed nawias, to wystarczy, że wymnożymy czynniki, np.: \[W(x) = 2x^2(2x + 3) = 2x^2 \cdot 2x + 2x^2 \cdot 3 = 4x^3 + 6x^2\]
Wyciągamy go przed nawias: \[W(x) = 4x^3 + 6x^2 = 2x^2(2x + 3)\] Uwaga! Jeżeli chcemy upewnić się, że dobrze wyciągnęliśmy wspólny czynnik przed nawias, to wystarczy, że wymnożymy czynniki, np.: \[W(x) = 2x^2(2x + 3) = 2x^2 \cdot 2x + 2x^2 \cdot 3 = 4x^3 + 6x^2\]
Rozłóż wielomian \(W(x) = 9x^3 - 3x^2 + 18x\) na czynniki.
Wspólnym czynnikiem każdego z trzech jednomianów tworzących ten wielomian jest \(3x\).
Wyciągamy go przed nawias: \[W(x) = 9x^3 - 3x^2 + 18x = 3x(3x^2 - x + 6)\]
Wyciągamy go przed nawias: \[W(x) = 9x^3 - 3x^2 + 18x = 3x(3x^2 - x + 6)\]
Rozłóż wielomian \(W(x) = 10x^5 - 2x^4 + 4x^3 + 12x^2\) na czynniki.
Wspólnym czynnikiem każdego z czterech jednomianów tworzących ten wielomian jest \(2x^2\).
Wyciągamy go przed nawias: \[W(x) = 10x^5 - 2x^4 + 4x^3 + 12x^2= 2x^2(5x^3 - x^2 + 2x + 6)\]
Wyciągamy go przed nawias: \[W(x) = 10x^5 - 2x^4 + 4x^3 + 12x^2= 2x^2(5x^3 - x^2 + 2x + 6)\]
Metoda wzorów skróconego mnożenia
Wzory skróconego mnożenia zostały dokładnie omówione w tym miejscu.Podczas rozkładania wielomianów na czynniki najczęściej wykorzystujemy wzór: \[a^2-b^2=(a-b)(a+b)\] Dla przypomnienia wypiszmy i ponumerujmy najczęściej stosowane wzory skróconego mnożenia: \[\begin{split} (1)\qquad &(a+b)^2=a^2+2ab+b^2\\[6pt] (2)\qquad &(a-b)^2=a^2-2ab+b^2\\[6pt] (3)\qquad &a^2-b^2=(a-b)(a+b)\\[6pt] (4)\qquad &a^3-b^3=(a-b)(a^2+ab+b^2)\\[6pt] (5)\qquad &a^3+b^3=(a+b)(a^2-ab+b^2)\\[6pt] (6)\qquad &(a+b)^3=a^3+3a^2b+3ab^2+b^3\\[6pt] (7)\qquad &(a-b)^3=a^3-3a^2b+3ab^2-b^3 \end{split}\]
Rozłóż wielomian \(W(x) = x^2 - 9\) na czynniki stosując wzory skróconego mnożenia.
Stosujemy wzór \((3)\): \[W(x) = x^2 - 9 = (x - 3)(x + 3)\]
Rozłóż wielomian \(W(x) = x^2 - 36\) na czynniki stosując wzory skróconego mnożenia.
Stosujemy wzór \((3)\): \[W(x) = x^2 - 36 = (x - 6)(x + 6)\]
Rozłóż na czynniki wielomian \(W(x) = x^2 + 6x + 9\).
Stosujemy wzór \((1)\): \[W(x) = x^2 + 6x + 9 = (x + 3)^2\]
Rozłóż na czynniki wielomian \(W(x) = x^2 - 10x + 25\).
Stosujemy wzór \((2)\): \[W(x) = x^2 - 10x + 25 = (x - 5)^2\]
Rozłóż na czynniki wielomian \(W(x) = x^3 - 27\).
Stosujemy wzór \((4)\): \[W(x) = x^3 - 27 = (x - 3)(x^2 + 3x + 9)\]
Rozłóż na czynniki wielomian \(W(x) = x^3 - 16x\).
W tym przykładzie możemy wyciągnąć wspólny czynnik przed nawias, więc zaczynamy od wykonania tego kroku: \[W(x) = x^3 - 16x = x(x^2 - 16)\] Teraz do wyrażenia w nawiasie stosujemy wzór \((3)\): \[W(x) = x(x^2 - 16) = x(x - 4)(x + 4)\]
Rozłóż na czynniki wielomian \(W(x) = 4x^4 - 36x^2\).
W tym przykładzie możemy wyciągnąć wspólny czynnik przed nawias, więc zaczynamy od wykonania tego kroku: \[W(x) = 4x^4 - 36x^2 = 4x^2(x^2 - 9)\] Teraz do wyrażenia w nawiasie stosujemy wzór \((3)\): \[W(x) = 4x^2(x^2 - 9) = 4x^2(x - 3)(x + 3)\]
Metoda delty
Metodę delty stosujemy do rozkładania na czynniki wyrażeń drugiego stopnia. W prostych przypadkach można posługiwać się wzorami skróconego mnożenia, np.: \[x^2 - 4 = (x - 2)(x + 2)\] W bardziej złożonych przykładach, np.: \(x^2 - x - 6\), ciężko jest zastosować wzory skróconego mnożenia i wtedy stosujemy metodę delty. Metoda delty - to zamiana postaci ogólnej wyrażenia kwadratowego na postać iloczynową. Zagadnienie to zostało omówione w dziale o postaciach funkcji kwadratowej.
Przypomnijmy jak robimy taką zamianę.Załóżmy, że mam do rozłożenia na czynniki następujący wielomian drugiego stopnia: \[W(x)=ax^2+bx+c\] Na początku liczymy deltę korzystając ze wzoru: \[\Delta =b^2-4ac\] Mogą zajść trzy przypadki:
- Jeżeli delta wyszła mniejsza od zera, to rozkład na czynniki nie istnieje.
- Jeżeli delta wyszła większa od zera, to istnieją miejsca zerowe wielomianu i możemy je obliczyć korzystając ze wzorów: \[\begin{split}{x}_{1}&=\frac{-b-\sqrt{\Delta }}{2a}\\{x}_{2}&=\frac{-b+\sqrt{\Delta }}{2a}\end{split}\] Postać iloczynowa wygląda wówczas tak: \[W(x)=a(x-x_1)(x-x_2)\]
- Jeżeli delta wyszła równa zero, to istnieje jedno miejsce zerowe i możemy je obliczyć ze wzoru: \[x_1=\frac{-b}{2a}\] Postać iloczynowa wielomianu wygląda wówczas tak: \[W(x)=a(x-x_1)^2\]
Rozłóż na czynniki wielomian \(W(x) = x^2 - x - 6\).
Zacznijmy od wypisania współczynników \(a\), \(b\), \(c\):
\[\begin{split}&a = 1\\[6pt] &b = -1\\[6pt] &c = -6\end{split}\]
Teraz liczymy deltę: \[\Delta = (-1)^2 - 4\cdot 1\cdot (-6) = 1 + 24 = 25\] Delta wyszła większa od zera, zatem mamy dwa miejsca zerowe: \[\begin{split} x_1=\frac{-b-\sqrt{\Delta }}{2a}=\frac{1-5}{2}=-2\\[6pt] x_2=\frac{-b+\sqrt{\Delta }}{2a}=\frac{1+5}{2}=3 \end{split}\] Zapisujemy postać iloczynową: \[W(x) = 1\cdot (x - 3)(x - (-2)) = (x - 3)(x + 2)\] Metoda grupowania wyrazów
Metodę grupowania wyrazów stosujemy najczęściej do rozkładania na czynniki wielomianów stopnia czwartego oraz wyższych.
Można powiedzieć, że jest to rozszerzenie metody wyciągania wspólnego czynnika przed nawias.Jeżeli np. we wzorze wielomianu występują \(4\) wyrazy, to możemy wyciągnąć przed nawias wspólny czynnik tylko z pierwszych dwóch wyrazów, a następnie wspólny czynnik z wyrazu trzeciego i czwartego. Spójrzmy na poniższy przykład:
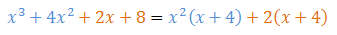W tym przykładzie zgrupowaliśmy pierwszy wyraz z drugim, a trzeci z czwartym. Następnie w ramach każdej grupy wyciągnęliśmy wspólny czynnik przed nawias.Z pierwszych dwóch wyrazów wyciągnęliśmy przed nawias wspólny czynnik \(x^2\), a z ostatnich dwóch wyrazów wyciągnęliśmy przed nawias liczbę \(2\). Tak się szczęśliwie złożyło, że w obu nawiasach pojawiło się to samo wyrażenie \(x + 4\). Dzięki temu można teraz wyciągnąć cały taki nawias przed nawias:
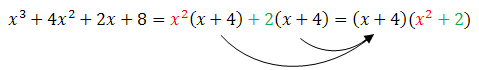W ten sposób rozłożyliśmy wielomian trzeciego stopnia na iloczyn czynników (nawiasu \((x^2 + 2)\) nie da się już bardziej rozłożyć, choćby dlatego, że delta dla niego wychodzi ujemna). Rozłóż na czynniki wielomian \(W(x) = 5x^3 + 10x^2 + 2x + 4\).
Grupujemy pierwszy wyraz z drugim, a trzeci z czwartym: \[\begin{split} W(x) &= 5x^3 + 10x^2 + 2x + 4 =\\[6pt] &=5x^2(x + 2) + 2(x + 2) = \\[6pt] &=(x + 2)(5x^2 + 2)\end{split}\] Z pierwszych dwóch wyrazów wyciągnęliśmy przed nawias wspólny czynnik \(5x^2\).
Z ostatnich dwóch wyrazów wyciągnęliśmy przed nawias liczbę \(2\).
W obu nawiasach otrzymaliśmy to samo wyrażenie \((x + 2)\), które następnie wyciągnęliśmy przed nawias. Ostatecznie otrzymaliśmy postać iloczynową wielomianu: \[W(x) = (x + 2)(5x^2 + 2)\] Uwaga! Należy jeszcze upewnić się, czy drugiego nawiasu nie da się rozłożyć na czynniki \(1\)-szego stopnia. Liczymy w tym celu deltę: \[\Delta = 0^2 - 4\cdot 5\cdot 2 = -40 \lt 0\] Delta wyszła ujemna, czyli nie istnieje rozkład nawiasu \((5x^2 + 2)\) na czynniki pierwszego stopnia.
Z ostatnich dwóch wyrazów wyciągnęliśmy przed nawias liczbę \(2\).
W obu nawiasach otrzymaliśmy to samo wyrażenie \((x + 2)\), które następnie wyciągnęliśmy przed nawias. Ostatecznie otrzymaliśmy postać iloczynową wielomianu: \[W(x) = (x + 2)(5x^2 + 2)\] Uwaga! Należy jeszcze upewnić się, czy drugiego nawiasu nie da się rozłożyć na czynniki \(1\)-szego stopnia. Liczymy w tym celu deltę: \[\Delta = 0^2 - 4\cdot 5\cdot 2 = -40 \lt 0\] Delta wyszła ujemna, czyli nie istnieje rozkład nawiasu \((5x^2 + 2)\) na czynniki pierwszego stopnia.
Rozłóż na czynniki wielomian \(W(x) = x^3 + 2x^2 - 9x - 18\).
Grupujemy pierwszy wyraz z drugim, a trzeci z czwartym: \[\begin{split} W(x) &= x^3 + 2x^2 - 9x - 18 =\\[6pt] &=x^2(x + 2) - 9(x + 2) =\\[6pt] &= (x + 2)(x^2 - 9) = \\[6pt] &=(x + 2)(x - 3)(x + 3) \end{split}\] W tym przykładzie drugi nawias można było rozłożyć na iloczyn czynników liniowych stosując wzór skróconego mnożenia. Ostatecznie otrzymaliśmy postać iloczynową wielomianu: \[W(x) = (x + 2)(x - 3)(x + 3)\]
W tym nagraniu wideo pokazuję na jak rozkładać wielomiany na iloczyn czynników.
Wielomian \(W(x)=x^6+x^3-2\) jest równy iloczynowi
A.\( (x^3+1)(x^2-2) \)
B.\( (x^3-1)(x^3+2) \)
C.\( (x^2+2)(x^4-1) \)
D.\( (x^4-2)(x+1) \)
Wielomian \(4x^2 - 100\) jest równy
A.\( (2x-10)^2 \)
B.\( (2x-10)(2x+10) \)
C.\( 4(x-10)^2 \)
D.\( 4(x-10)(x+10) \)
Rozłóż wielomian \(W(x)=x^4+5x^2-x^3-5x\) na czynniki możliwie najniższego stopnia.
Rozkładając wielomian \(W(x) = x^3 - 2x^2 - 9x + 18\) na czynniki liniowe otrzymamy wielomian
A.\( (x+2)(x-3)(x+3) \)
B.\( (x+3)(x-2)(x-3) \)
C.\( (x-2)(x-3)(x+2) \)
D.\( (x+2)(x+3)(x-2) \)
Wielomian \(W(x) = x^3 + 7x^2 - 2x - 14\) po rozłożeniu na czynniki ma postać
A.\( W(x)=(x^2+2)(x+7) \)
B.\( W(x)=(x+7)(x+2)(x-2) \)
C.\( W(x)=(x+7)(x-\sqrt{2})(x+\sqrt{2}) \)
D.\( W(x)=(x-7)(x-\sqrt{2})(x+\sqrt{2}) \)
Rozkład wielomianu \(W(x) = x^3 - 2x^2 - 16x + 32\) na czynniki liniowe to
A.\( (x-4)(x-4)(x-2) \)
B.\( (x-4)(x-2)(x+4) \)
C.\( (x+4)(x+2)(x+4) \)
D.\( (x-4)(x+4)(x+2) \)
Przedstawieniem wyrażenia \(4 - x^2 + 2xy - y^2\) w postaci iloczynu jest
A.\( ((x-y)-2)((x-y)+2) \)
B.\( ((x-y)-2)^2 \)
C.\( -((x-y)-2)((x-y)+2) \)
D.\( ((x-y)+2)^2 \)
Wyrażenie \(x^2-xy-2y+2x\) rozłożone na czynniki ma postać
A.\( (x-y)(x+2) \)
B.\( (x-y)(x-2) \)
C.\( (x+y)(x+2) \)
D.\( (x+y)(x-2) \)
Rozłóż na czynniki możliwie najniższego stopnia, wielomian: \(x^3+2x^2-9x-18\).
Wielomian \(W(x)\) jest stopnia czwartego. Pierwiastkiem dwukrotnym tego wielomianu jest liczba \(-1\). Po rozłożeniu na czynniki wielomian ten może być postaci:
A.\( -2(x-1)^2(x^2+1) \)
B.\( (x+1)^2(x-4) \)
C.\( -(x+1)^2(x^2+3) \)
D.\( (x-1)(x+1)(x+2)(x-3) \)