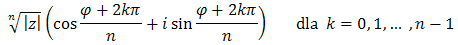Pierwiastkowanie liczb zespolonych
Gdy pierwiastkujemy liczby zespolone, to możemy otrzymać kilka różnych wyników.
Na przykład pierwiastkiem 4 stopnia z liczby 1 są liczby: 1, -1, i oraz -i, ponieważ:
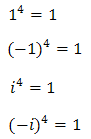
Zatem wyciągając pierwiastek 4 stopnia z liczby rzeczywistej 1, mamy w liczbach zespolonych aż 4 rozwiązania!
Generalnie gdy wyciągamy pierwiastek n-tego stopnia z liczby zespolonej, to zawsze otrzymujemy n rozwiązań. O tym jak obliczyć te rozwiązania mówi następujące twierdzenie:
Wówczas pierwiastkami stopnia n z liczby z są liczby: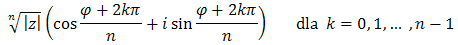
Na przykład pierwiastkiem 4 stopnia z liczby 1 są liczby: 1, -1, i oraz -i, ponieważ:
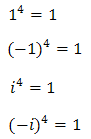
Zatem wyciągając pierwiastek 4 stopnia z liczby rzeczywistej 1, mamy w liczbach zespolonych aż 4 rozwiązania!
Generalnie gdy wyciągamy pierwiastek n-tego stopnia z liczby zespolonej, to zawsze otrzymujemy n rozwiązań. O tym jak obliczyć te rozwiązania mówi następujące twierdzenie:
Twierdzenie
Niech z = |z|(cosφ + i sinφ) będzie liczbą zespoloną różną od zera.Wówczas pierwiastkami stopnia n z liczby z są liczby: