Pewniaki do matury rozszerzonej 2024
Pewniaki do matury 2024!
Strona zawiera typy zadań, które mają największą szansę pojawić się na maturze rozszerzonej w nowej formule (od 2023 roku).
Wybrane typy zadań stanowią ok 27 punktów do zdobycia na maturze.
Strona zawiera typy zadań, które mają największą szansę pojawić się na maturze rozszerzonej w nowej formule (od 2023 roku).
Wybrane typy zadań stanowią ok 27 punktów do zdobycia na maturze.
Jak wybrałem pewniaki?
Pewniaki to są typy zadań, które pojawiły się na wszystkich 3 ostatnich oficjalnych arkuszach rozszerzonych od CKE (marzec 2023, maj 2023, czerwiec 2023).
Pewniaki to są typy zadań, które pojawiły się na wszystkich 3 ostatnich oficjalnych arkuszach rozszerzonych od CKE (marzec 2023, maj 2023, czerwiec 2023).
Pełną wiedzę niezbędną do zdania matury na 100% znajdziesz w kursie do nowej matury rozszerzonej.
Typ I - zamiana podstaw logarytmów [2-3 punkty]
Na maturze z maja 2023 nie pojawiło się bezpośrednie zadanie z logarytmów, ale było ono częścią składową większego zadania optymalizacyjnego, które jeszcze pojawi się w dalszej części tego zestawienia.
Dane są liczby \(a = \log_23\) oraz \(b = \log_37\).
Wyraź \(\log_449\) za pomocą liczb \(a\) oraz \(b\).
Zapisz obliczenia.
Dane są liczby \[a=4^{\log_245}\ \ \ \text{oraz}\ \ \ b=\frac{\log_32023}{\log_92023}\]
Oblicz \(a-b\).
Typ II - styczna do wykresu funkcji [3 punkty]
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{x^2+3}{x-1}\) dla każdej liczby rzeczywistej \(x \ne 1\).
Wyznacz równanie stycznej do wykresu tej funkcji w punkcie \(P=(-3,-3)\).
Zapisz obliczenia.
Funkcja \(f\) jest określona wzorem \(f(x) = \frac{3x^2-2x}{x^2+2x+8}\) dla każdej liczby rzeczywistej \(x\). Punkt \(P = (x_0, 3)\) należy do wykresu funkcji \(f\).
Oblicz \(x_0\) oraz wyznacz równanie stycznej do wykresu funkcji \(f\) w punkcie \(P\). Zapisz obliczenia.
Funkcja \(f\) jest określona wzorem \(f(x) = 2x^3-4x^2+9x\) dla każdego \(x\in \mathbb{R} \). Punkt \(P = (x_0, 18)\) należy do wykresu funkcji \(f\).
Oblicz \(x_0\) oraz wyznacz równanie stycznej do wykresu funkcji \(f\) w punkcie \(P\). Zapisz obliczenia.
Typ III - szereg geometryczny [4 punkty]
Dany jest nieskończony ciąg geometryczny \((a_n)\), określony dla każdej liczby naturalnej \(n \ge 1\). Suma trzech początkowych wyrazów ciągu \((a_n)\) jest równa \(7\), a suma \(S\) wszystkich wyrazów tego ciągu jest równa \(8\).
Wyznacz wszystkie wartości \(n\), dla których spełniona jest nierówność \[\left|\frac{S-S_n}{S_n}\lt0{,}001\right|\] gdzie \(S_n\) oznacza sumę \(n\) początkowych wyrazów ciągu \((a_n)\).
Zapisz obliczenia.
Zapisz obliczenia.
Określamy kwadraty \(K_1, K_2, K3_,...\) następująco: 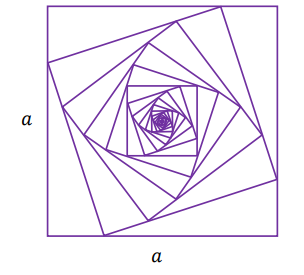
- \(K_1\) jest kwadratem o boku długości \(a\)
- \(K_2\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_1\) i dzieli ten bok w stosunku \(1 ∶ 3\)
- \(K_3\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_2\) i dzieli ten bok w stosunku \(1 ∶ 3\)
- \(K_n\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_{n-1}\) i dzieli ten bok w stosunku \(1 ∶ 3\).

Oblicz sumę wszystkich wyrazów tego nieskończonego ciągu. Zapisz obliczenia.
Dany jest nieskończony szereg geometryczny \[2x-\frac{6x}{x-1}+\frac{18x}{(x-1)^2}-\frac{54x}{(x-1)^3}+\ ...\]
Wyznacz wszystkie wartości zmiennej \(x\) (różnej od \(0\) i od \(1\)), dla których suma tego szeregu istnieje i jest równa \(\frac{15}{2}\). Zapisz obliczenia.
Typ IV - równanie kwadratowe z parameterem \(m\) [5 punktów]
Dane jest równanie \((x - 6) ⋅ \bigl[(m - 2)x^2 - 4(m + 3)x + m + 1\bigl] = 0\) z niewiadomą \(x\) i parametrem \(m\in \mathbb{R}\).
Wyznacz wszystkie wartości parametru \(m\), dla których to równanie ma trzy różne rozwiązania rzeczywiste tego samego znaku.
Zapisz obliczenia.
Wyznacz wszystkie wartości parametru \(m\ne 2\), dla których równanie \[x^2+4x-\frac{m-3}{m-2}=0\] ma dwa różne rozwiązania rzeczywiste \(x_1, x_2\) spełniające warunek \(x_1^3+x_2^3\gt-28\). Zapisz obliczenia.
Wyznacz wszystkie wartości parametru \(m\), dla których równanie \[mx^2-(m+1)x-2m+3=0\] ma dokładnie dwa różne rozwiązania rzeczywiste \(x_1\) oraz \(x_2\), spełniające warunki: \[x_1\ne 0, \ \ \ x_2\ne 0\ \ \ \text{oraz}\ \ \ \frac{1}{x_1^2}+\frac{1}{x_2^2} \lt 1\] Zapisz obliczenia.
Typ V - równanie trygonometryczne [3-4 punkty]
Rozwiąż równanie \[\sin (3x)=2\sin x\] w zbiorze \([0,\pi ]\).
Rozwiąż równanie \[4\sin(4x)\cos(6x)=2\sin(10x)+1\]
Rozwiąż równanie \[\sin(5x)+\cos x=0\] w zbiorze \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\). Zapisz obliczenia.
Typ VI - schemat Bernoullego [3-4 punkty]
Egzamin składa się z \(15\) zadań zamkniętych. Do każdego zadania podano cztery odpowiedzi, z których tylko jedna okazuje się poprawna. Zdający zalicza egzamin, jeśli udzieli poprawnych odpowiedzi w co najmniej \(11\) zadaniach. Pewien student przystąpił nieprzygotowany do egzaminu i w każdym zadaniu wybierał losowo odpowiedź. Przyjmij, że w każdym zadaniu wybór każdej z odpowiedzi przez studenta jest równo prawdopodobny.
Oblicz prawdopodobieństwo zdarzenia, że ten student zaliczył egzamin.
Zapisz obliczenia.
Tomek i Romek postanowili rozegrać między sobą pięć partii szachów. Prawdopodobieństwo wygrania pojedynczej partii przez Tomka jest równe \(\frac{1}{4}\).
Oblicz prawdopodobieństwo wygrania przez Tomka co najmniej czterech z pięciu partii. Wynik podaj w postaci ułamka zwykłego nieskracalnego. Zapisz obliczenia.
Prawdopodobieństwo wystąpienia awarii sieci ciepłowniczej na pewnym osiedlu mieszkaniowym w godzinach porannych pojedynczego dnia jest równe \(0{,}1\).
Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że w okresie siedmiu dni wystąpią co najwyżej dwa takie dni, w których nastąpi awaria tej sieci na tym osiedlu w godzinach porannych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych. Zapisz obliczenia.
Typ VII - zadanie optymalizacyjne [6 punktów]
Na obrzeżach miasta znajduje się jezioro, na którym postanowiono stworzyć tor regatowy. Na podstawie dostępnych map wymodelowano w pewnej skali kształt linii brzegowej jeziora w kartezjańskim układzie współrzędnych \((x, y)\) za pomocą fragmentów wykresów funkcji \(f\) oraz \(g\) (zobacz rysunek). Funkcje \(f\) oraz \(g\) są określone wzorami \(f(x) = x^2\) oraz \(g(x)=-\frac{1}{2}\left(x-\frac{1}{2}\right)^2+4\). Początek toru postanowiono zlokalizować na brzegu jeziora w miejscu, któremu odpowiada w układzie współrzędnych punkt \(P = (-1, 1)\). 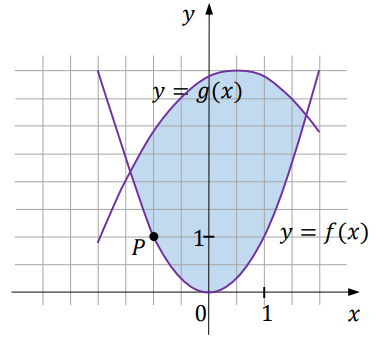

Niech \(R\) będzie punktem leżącym na wykresie funkcji \(g\).
Wykaż, że odległość punktu \(R\) od punktu \(P\) wyraża się wzorem \[|PR|=\sqrt{\frac{1}{4}x^4-\frac{1}{2}x^3-\frac{13}{8}x^2+\frac{39}{8}x+\frac{593}{64}}\] gdzie \(x\) jest pierwszą współrzędną punktu \(R\).
Koniec toru regatowego należy umieścić na linii brzegowej.
Oblicz współrzędne punktu \(K\), w którym należy zlokalizować koniec toru, aby długość toru (tj. odległość końca \(K\) toru od początku \(P\)) była możliwie największa. Oblicz długość najdłuższego toru.
Zapisz obliczenia.
Wskazówka.
Przy rozwiązywaniu zadania możesz skorzystać z tego, że odległość dowolnego punktu \(R\) leżącego na wykresie funkcji \(g\) od punktu \(P\) wyraża się wzorem \[|PR|=\sqrt{\frac{1}{4}x^4-\frac{1}{2}x^3-\frac{13}{8}x^2+\frac{39}{8}x+\frac{593}{64}}\] gdzie \(x\) jest pierwszą współrzędną punktu \(R\).
Przy rozwiązywaniu zadania możesz skorzystać z tego, że odległość dowolnego punktu \(R\) leżącego na wykresie funkcji \(g\) od punktu \(P\) wyraża się wzorem \[|PR|=\sqrt{\frac{1}{4}x^4-\frac{1}{2}x^3-\frac{13}{8}x^2+\frac{39}{8}x+\frac{593}{64}}\] gdzie \(x\) jest pierwszą współrzędną punktu \(R\).
Funkcja \(f\) jest określona wzorem \(f(x) = 81^{\log_3x}+\frac{2\cdot \log_2\sqrt{27}\cdot \log_32}{3}\cdot x^2-6x\) dla każdej liczby dodatniej \(x\).
Wykaż, że dla każdej liczby dodatniej \(x\) wyrażenie \[81^{\log_3x}+\frac{2\cdot \log_2\sqrt{27}\cdot \log_32}{3}\cdot x^2-6x\] można równoważnie przekształcić do postaci \(x^4+x^2-6x\).
Oblicz najmniejszą wartość funkcji \(f\) określonej dla każdej liczby dodatniej \(x\). Zapisz obliczenia.
Wskazówka: przyjmij, że wzór funkcji \(f\) można przedstawić w postaci \(f(x) = x^4 + x^2 - 6x\).
Rozważamy wszystkie graniastosłupy prawidłowe czworokątne \(ABCDEFGH\), w których odcinek łączący punkt \(O\) przecięcia przekątnych \(AC\) i \(BD\) podstawy \(ABCD\) z dowolnym wierzchołkiem podstawy \(EFGH\) ma długość \(d\) (zobacz rysunek). Zapisz obliczenia.
Wyznacz zależność objętości \(V\) graniastosłupa od jego wysokości \(h\) i podaj dziedzinę funkcji \(V(h)\).
Wyznacz wysokość tego z rozważanych graniastosłupów, którego objętość jest największa.
Typ VIII - Inne ważne zagadnienia
- zadania z geometrii na wykorzystanie twierdzenia sinusów lub cosinusów
- zadania z geometrii analitycznej wykorzystujące równanie okręgu
- zadania na udowadnianie nierówności
Tematy nadrzędne i sąsiednie



