Otoczenie punktu i punkt skupienia
Definicja
Punkt \(x_0\) jest punktem skupienia zbioru liczbowego \(X\), jeżeli dowolnie blisko \(x_0\) znajduje się nieskończenie wiele liczb ze zbioru \(X\). Liczba \(5\) jest punktem skupienia zbioru liczb rzeczywistych \(\mathbb{R} \), ponieważ dowolne blisko punktu \(5\) znajduje nieskończenie wiele liczb rzeczywistych.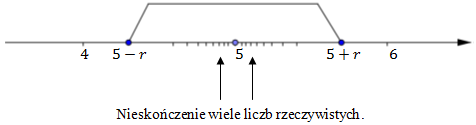 
Dowolna inna liczba rzeczywista jest również punktem skupienia zbioru \(\mathbb{R} \).
Dowolna inna liczba rzeczywista jest również punktem skupienia zbioru \(\mathbb{R} \). Liczba \(5\) nie jest punktem skupienia zbioru liczb naturalnych \(\mathbb{N} \), ponieważ w otoczeniu punktu \(5\) o promieniu \(r\lt 1\) nie znajduje się już żadna inna liczba naturalna różna od \(5\).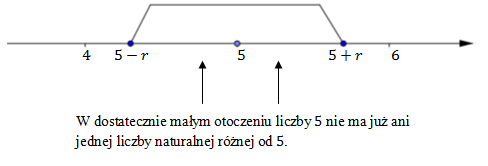 
Zbiór liczb naturalnych \(\mathbb{N} \) nie ma punktów skupienia.
Zbiór liczb naturalnych \(\mathbb{N} \) nie ma punktów skupienia. W powyższych przykładach pojawiło się pojęcie otoczenia punktu. Podamy teraz jego formalną definicję.
Definicja
Otoczeniem \(U(x_0;r)\) punktu \(x_0\) nazywamy przedział otwarty \((x_0 - r , x_0 + r)\) o środku w punkcie \(x_0\). Wykorzystując pojęcie otoczenia punktu możemy teraz podać formalną definicję punktu skupienia.
Definicja
Punkt \(x_0\) jest punktem skupienia zbioru \(X\), jeżeli w dowolnym otoczeniu punktu \(x_0\) istnieje nieskończenie wiele wartości z \(X\). Sam punkt skupienia może należeć do zbioru \(X\) lub nie.
Każda liczba wymierna jest punktem skupienia zbioru liczb wymiernych \(\mathbb{Q} \).
Liczba \(\sqrt{2}\) jest punktem skupienia zbioru liczb wymiernych \(\mathbb{Q} \), pomimo, że nie należy do tego zbioru.
W dowolnie małym otoczeniu \(\sqrt{2}\) można bez trudu wskazać nieskończenie wiele liczb wymiernych.
W dowolnie małym otoczeniu \(\sqrt{2}\) można bez trudu wskazać nieskończenie wiele liczb wymiernych.
W każdym otoczeniu liczby \(\sqrt{2}\) jest nieskoczenie wiele liczb wymiernych.
Każda liczba rzeczywista jest punktem skupienia zbioru liczb wymiernych.