Ostrosłup prawidłowy czworokątny
Poziom podstawowy
Ostrosłup prawidłowy czworokątny - to taki ostrosłup, który ma w podstawie czworokąt foremny, czyli kwadrat. Wierzchołek takiego ostrosłupa leży dokładnie nad środkiem podstawy. W związku z tym ostrosłup prawidłowy czworokątny ma cztery identyczne ściany boczne, które są trójkątami równoramiennymi.
Spodek wysokości ostrosłupa leży na przecięciu przekątnych kwadratu w podstawie.
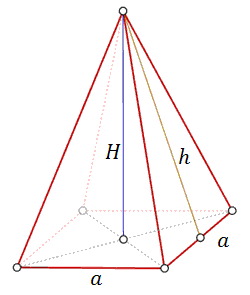
Wzór na pole powierzchni ostrosłupa prawidłowego czworokątnego: \[P_c=P_p+P_b=a^2+4\cdot \frac{1}{2}ah=a^2+2ah\] gdzie:
\(P_p\) - pole podstawy ostrosłupa
\(P_b\) - suma pól ścian bocznych ostrosłupa
Wzór na objętość ostrosłupa prawidłowego czworokątnego: \[V=\frac{1}{3}\cdot P_p\cdot H=\frac{1}{3} a^2 H\] gdzie:\(P_p\) - pole podstawy ostrosłupa
\(P_b\) - suma pól ścian bocznych ostrosłupa
\(P_p\) - pole podstawy ostrosłupa
\(H\) - wysokość ostrosłupa
Zadanie 1.
Na rysunku przedstawiono fragment siatki ostrosłupa prawidłowego czworokątnego.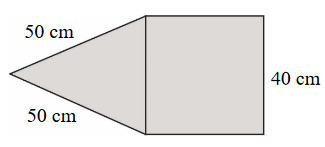 
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Suma długości wszystkich krawędzi tego ostrosłupa jest równa A.\( 560 \) cm
B.\( 360 \) cm
C.\( 260 \) cm
D.\( 220 \) cm
Zadanie 2.
Kąt \(\alpha \) nachylenia ściany bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy zaznaczony jest na rysunku: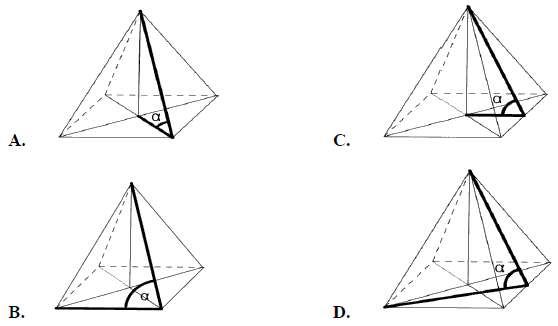 
Zadanie 3.
W ostrosłupie prawidłowym czworokątnym krawędź boczna ma długość \(5\) cm, a krawędź podstawy \(\sqrt{8}\) cm. Wówczas cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy jest równy:
A.\( \frac{\sqrt{2}}{5} \)
B.\( 0{,}6 \)
C.\( 0{,}4 \)
D.\( \frac{\sqrt{8}}{10} \)
Zadanie 4.
Pole podstawy ostrosłupa prawidłowego czworokątnego jest równe \(100\) cm2, a jego pole powierzchni bocznej jest równe \(260\) cm2. Oblicz objętość tego ostrosłupa.
Zadanie 5.
W ostrosłupie prawidłowym czworokątnym \(ABCDS\) o podstawie \(ABCD\) i wierzchołku \(S\) trójkąt \(ACS\) jest równoboczny i ma bok długości \(8\). Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa (zobacz rysunek).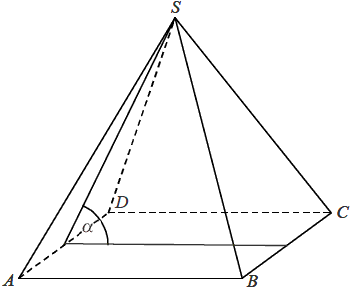 
Zadanie 6.
W graniastosłupie prawidłowym czworokątnym \(ABCDEFGH\) przekątna \(AC\) podstawy ma długość \(4\). Kąt \(ACE\) jest równy \(60^\circ\). Oblicz objętość ostrosłupa \(ABCDE\) przedstawionego na poniższym rysunku.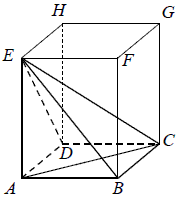 
Zadanie 7.
Piramida Cheopsa ma kształt ostrosłupa prawidłowego czworokątnego. Każda ściana boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem \(52^\circ \), a pole powierzchni ściany bocznej jest równe \(21\ 550 \) m2. Oblicz objętość piramidy. Wynik zapisz w postaci \(a\cdot 10k\), gdzie \(1\le a\lt 10\) i \(k\) jest liczbą całkowitą.
Zadanie 8.
Piramida ma kształt ostrosłupa prawidłowego czworokątnego, którego wysokość jest równa \(6\), a długość krawędzi bocznej jest równa \(2\sqrt{15}\). Oblicz miarę kąta nachylenia ściany bocznej piramidy do podstawy.
Zadanie 9.
Podstawą ostrosłupa prawidłowego czworokątnego \(ABCDS\) jest kwadrat \(ABCD\) (zobacz rysunek). Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta \(SAC\) jest równa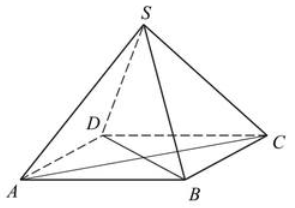 
A.\( 60^\circ \)
B.\( 45^\circ \)
C.\( 90^\circ \)
D.\( 75^\circ \)
Zadanie 10.
W ostrosłupie prawidłowym czworokątnym objętość jest równa \(32\), zaś krawędź podstawy jest równa \(4\). Wysokość tego ostrosłupa jest równa:
A.\( \frac{2}{3} \)
B.\( \frac{4}{3} \)
C.\( 2 \)
D.\( 6 \)
Zadanie 11.
Drut o długości \(96\) cm wykorzystano w całości na wykonanie szkieletu ostrosłupa prawidłowego czworokątnego o wszystkich krawędziach równej długości. Zaznacz na rysunku kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny podstawy i wyznacz cosinus tego kąta.
Zadanie 12.
Podstawą ostrosłupa prawidłowego jest kwadrat. Wysokość ściany bocznej tego ostrosłupa jest równa \( 22 \), a tangens kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy jest równy \( \frac{4\sqrt{6}}{5} \). Oblicz objętość tego ostrosłupa.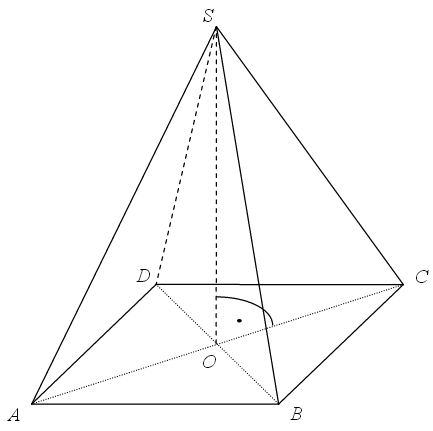 
Zadanie 13.
Rysunek przedstawia ostrosłup prawidłowy czworokątny \(ABCDS\).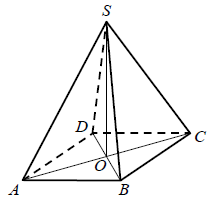 
Kątem między krawędzią \(CS\) a płaszczyzną podstawy tego ostrosłupa jest kąt
Kątem między krawędzią \(CS\) a płaszczyzną podstawy tego ostrosłupa jest kąt A.\( DCS \)
B.\( ACS \)
C.\( OSC \)
D.\( SCB \)
Zadanie 14.
W ostrosłupie prawidłowym czworokątnym ściana boczna o polu równym \(10\) jest nachylona do płaszczyzny podstawy pod kątem \(60^\circ\). Oblicz objętość tego ostrosłupa.
Zadanie 15.
Dany jest ostrosłup prawidłowy czworokątny \(ABCDS\), którego ściany boczne są trójkątami równobocznymi. Punkty \(G\), \(E\) i \(F\) są odpowiednio środkami odcinków \(AD\), \(BC\) i \(CS\) (zobacz rysunek).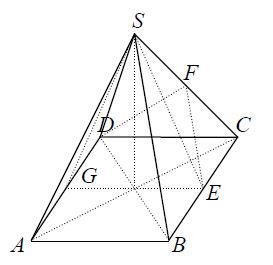 
Kątem między przeciwległymi ścianami bocznymi jest kąt
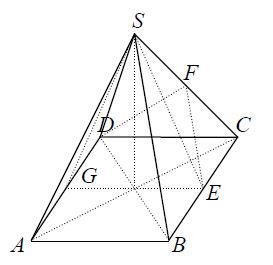Kątem między przeciwległymi ścianami bocznymi jest kąt A.\( DFE \)
B.\( GES \)
C.\( ESG \)
D.\( ASC \)
Zadanie 16.
W ostrosłupie prawidłowym czworokątnym kąt pomiędzy wysokością ostrosłupa a wysokością ściany bocznej jest równy \(30^\circ \). Promień okręgu opisanego na podstawie jest równy \(2\sqrt{2}\). Oblicz sinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
Zadanie 17.
Dany jest ostrosłup prawidłowy czworokątny, którego wysokość ma długość \(H\) oraz kąt między krawędzią boczną i płaszczyzną podstawy jest równy \(60^\circ \). Wyznacz wzór na pole powierzchni bocznej tego ostrosłupa w zależności od wysokości \(H\).
Zadanie 18.
Podstawą ostrosłupa prawidłowego czworokątnego \(ABCDS\) jest kwadrat \(ABCD\). Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta \(ASC\) jest równa
A.\( 45^\circ \)
B.\( 30^\circ \)
C.\( 75^\circ \)
D.\( 90^\circ \)
Zadanie 19.
Na rysunku przedstawiono ostrosłup prawidłowy czworokątny \(ABCDS\) o podstawie \(ABCD\).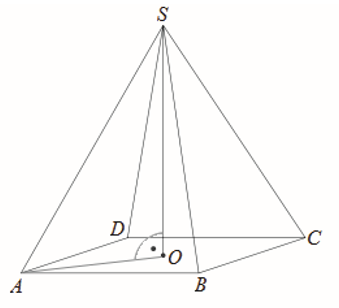 
Kąt nachylenia krawędzi bocznej \(SA\) ostrosłupa do płaszczyzny podstawy \(ABCD\) to
Kąt nachylenia krawędzi bocznej \(SA\) ostrosłupa do płaszczyzny podstawy \(ABCD\) to A.\( \sphericalangle SAO \)
B.\( \sphericalangle SAB \)
C.\( \sphericalangle SOA \)
D.\( \sphericalangle ASB \)
Zadanie 20.
Dany jest ostrosłup prawidłowy czworokątny o wysokości \(H=16\). Cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy \(\frac{3}{5}\). Oblicz pole powierzchni bocznej tego ostrosłupa.
Zadanie 21.
Wysokość ostrosłupa prawidłowego czworokątnego jest równa \(8\). Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem \(40^\circ \). Oblicz objętość tego ostrosłupa.
Zadanie 22.
Krawędź podstawy ostrosłupa prawidłowego czworokątnego jest równa \(\sqrt{2}\). Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 6\(0^\circ \). Oblicz objętość tego ostrosłupa.
Zadanie 23.
Krawędź podstawy ostrosłupa prawidłowego czworokątnego jest równa \(1\), a wysokość jest równa \(2\). Oblicz pole powierzchni całkowitej tego ostrosłupa.
Zadanie 24.
Podstawą ostrosłupa prawidłowego czworokątnego \(ABCDS\) jest kwadrat \(ABCD\). Pole trójkąta równoramiennego \(ACS\) jest równe \(120\) oraz \(|AC| : |AS| = 10 : 13\) . Oblicz pole powierzchni bocznej tego ostrosłupa.
Zadanie 25.
Długość krawędzi podstawy ostrosłupa prawidłowego czworokątnego jest równa \(6\). Pole powierzchni całkowitej tego ostrosłupa jest cztery razy większe od pola jego podstawy. Kąt \(\alpha\) jest kątem nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy (zobacz rysunek). Oblicz cosinus kąta \(\alpha\).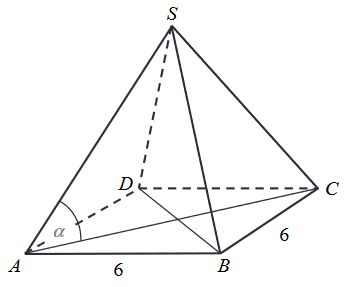 
Zadanie 26.
Długość krawędzi bocznej ostrosłupa prawidłowego czworokątnego \(ABCDS\) jest równa \(12\). (zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt \(\alpha \) taki, że \(\operatorname{tg} \alpha =\frac{2}{\sqrt{5}}\). Oblicz objętość tego ostrosłupa.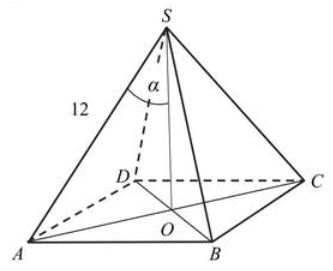 
Poziom rozszerzony
Zadanie 27.
Kąt dwuścienny zawarty między sąsiednimi ścianami bocznymi ostrosłupa prawidłowego czworokątnego ma miarę \(2\alpha\). Wyznacz sinus kąta nachylenia ściany bocznej tego ostrosłupa do jego podstawy.
Zadanie 28.
W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość \(a\). Ostrosłup ten przecięto płaszczyzną przechodzącą przez środki dwóch sąsiednich krawędzi podstawy i wierzchołek ostrosłupa. Płaszczyzna tego przekroju tworzy z płaszczyzną podstawy kąt o mierze \(\alpha\). Oblicz objętość tego ostrosłupa.
Zadanie 29.
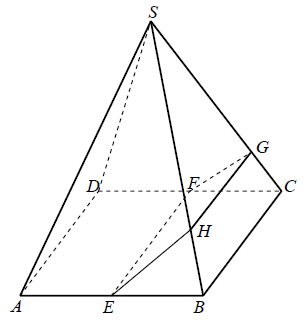
Punkt \(S\) jest wierzchołkiem ostrosłupa prawidłowego czworokątnego, a punkty \(E\), \(F\) są odpowiednio środkami krawędzi \(AB\) i \(CD\) jego podstawy. Krawędź podstawy i wysokość tego ostrosłupa mają taką samą długość równą \(1\). Płaszczyzna przechodząca przez punkty \(E\) i \(F\) przecina krawędzie boczne odpowiednio w punktach \(G\) oraz \(H\) (zobacz rysunek). Oblicz pole otrzymanego przekroju, wiedząc, że jest ono dwa razy większe od pola czworokąta \(BCGH\). 
Zadanie 30.
W ostrosłupie prawidłowym czworokątnym \(ABCDS\) o podstawie \(ABCD\) wysokość jest równa \(5\), a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę \(120^\circ \). Oblicz objętość tego ostrosłupa.