Okrąg wpisany w trójkąt
W każdy trójkąt można wpisać okrąg.
Środek okręgu wpisanego leży na przecięciu dwusiecznych trójkąta: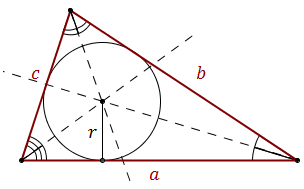
Środek okręgu wpisanego leży na przecięciu dwusiecznych trójkąta:

Promień okręgu wpisanego można obliczyć ze wzoru: \[r=\sqrt{\frac{(p-a)(p-b)(p-c)}{p}}\] gdzie \(p\) - to połowa obwodu trójkąta, czyli \(p=\frac{a+b+c}{2}\).
W przypadku gdy znamy promień okręgu opisanego (\(R\)), to promień okręgu wpisanego można obliczyć ze wzoru: \[r=\frac{abc}{4Rp}\]
Dany jest trójkąt prostokątny \(ABC\), w którym \(|BC| = 30\), \(|AC| = 40\), \(|AB| = 50\). Punkt \(W\) jest środkiem okręgu wpisanego w ten trójkąt. Okrąg wpisany w trójkąt \(ABC\) jest styczny do boku \(AB\) w punkcie \(M\). Oblicz długość odcinka \(CM\). 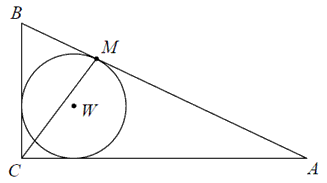

Długość boku trójkąta równobocznego jest równa \(24\sqrt{3}\). Promień okręgu wpisanego w ten trójkąt jest równy
A.\( 36 \)
B.\( 18 \)
C.\( 12 \)
D.\( 6 \)
Okrąg wpisany w trójkąt prostokątny \(ABC\) jest styczny do przeciwprostokątnej \(AB\) w punkcie \(K\). Wiadomo, że \(|AK| = 4\) i \(|KB| = 6\). Oblicz promień tego okręgu.