Okrąg opisany na trójkącie

Drukuj

Poziom podstawowy

Na każdym trójkącie można opisać okrąg.
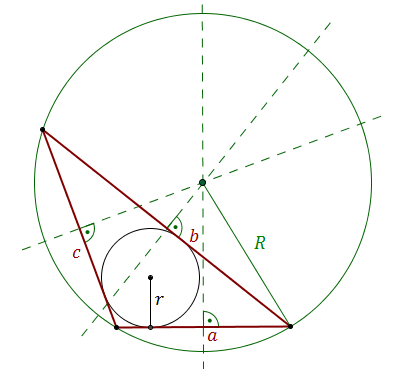
Środek okręgu opisanego leży na przecięciu symetralnych boków trójkąta:

Promień okręgu opisanego można obliczyć ze wzoru: \[R=\frac{abc}{4rp}\] gdzie:

\(a\), \(b\), \(c\) - to długości boków trójkąta,
\(r\) - to długość promienia okręgu wpisanego w trójkąt,
\(p\) - to połowa obwodu trójkąta, czyli \(p=\frac{a+b+c}{2}\).

Punkt \(S\) jest środkiem okręgu opisanego na trójkącie ostrokątnym \(ABC\). Kąt \(ACS\) jest trzy razy większy od kąta \(BAS\), a kąt \(CBS\) jest dwa razy większy od kąta \(BAS\). Oblicz kąty trójkąta \(ABC\).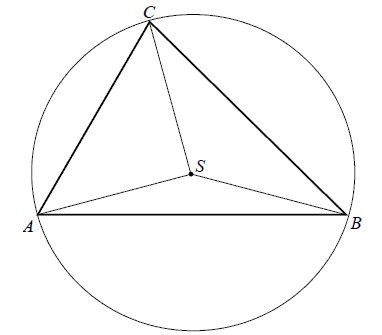

\(45^\circ , 60^\circ , 75^\circ \)

Okrąg opisany na trójkącie równobocznym ma promień \(12\). Wysokość tego trójkąta jest równa

A.\( 18 \)

B.\( 20 \)

C.\( 22 \)

D.\( 24 \)

Promień okręgu opisanego na trójkącie prostokątnym jest równy \(2\sqrt{5}\). Jedna z przyprostokątnych tego trójkąta jest o \(4\) dłuższa od drugiej przyprostokątnej. Oblicz wysokość tego trójkąta opuszczoną na przeciwprostokątną.

\(h=\frac{8\sqrt{5}}{5}\)

Promień okręgu opisanego na trójkącie równobocznym jest równy \( \frac{16\sqrt{3}}{3} \). Obwód tego trójkąta jest równy

A.\(16\)

B.\(32\)

C.\(48\)

D.\(64\)

Pole koła opisanego na trójkącie równobocznym o wysokości \(9\) jest równe

A.\( 36\pi \)

B.\( 9\pi \)

C.\( 18\sqrt{3}\pi \)

D.\( 12\pi \)

W trójkącie równobocznym \(ABC\) dana jest wysokość \(|CD|=3\). Średnica okręgu opisanego na tym trójkącie ma długość:

A.\( 4 \)

B.\( \frac{2\sqrt{3}}{3} \)

C.\( \frac{4\sqrt{3}}{3} \)

D.\( 2 \)

Dany jest trójkąt prostokątny o przyprostokątnych \(5\) i \(12\). Promień okręgu opisanego na tym trójkącie jest równy

A.\( 12 \)

B.\( 8{,}5 \)

C.\( 6{,}5 \)

D.\( 5 \)