Nierówności z wartością bezwzględną

Zadania z nierówności z wartością bezwzględną są również w dziale Interpretacja geometryczna wartości bezwzględnej.

Wskaż liczbę, która spełnia nierówność \(|3x-4|\le x+1\).

A. \(-2\)

B. \(-1\)

C. \(0\)

D. \(1\)

Zbiór \((-\infty ,-8\rangle \cup \langle -4,+\infty )\) jest rozwiązaniem nierówności:

A.\( |x-6|\le 2 \)

B.\( |x-6|\ge 2 \)

C.\( |x+6|\le 2 \)

D.\( |x+6|\ge 2 \)

Ile rozwiązań w zbiorze liczb rzeczywistych ma nierówność: \(|x+3| \le 0\)?

A.\( 0 \)

B.\( 1 \)

C.\( 2 \)

D.nieskończenie wiele

Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności \(|x + 4| \le 7\).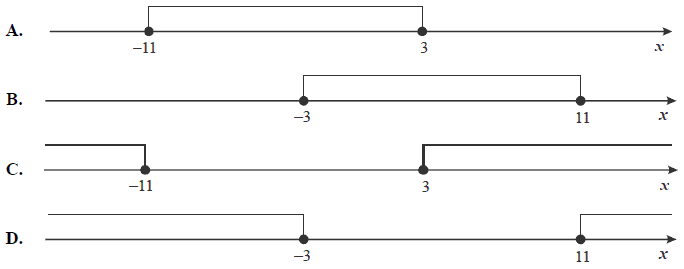

Wskaż liczbę, która spełnia nierówność \( |1 - 2x| \lt x \)

A.\( x=0 \)

B.\( x=0{,}5 \)

C.\( x=1 \)

D.\( x=2 \)

Wskaż nierówność, którą spełnia liczba \(5\sqrt{3}\)

A.\( |x-1|\lt 2 \)

B.\( |x-2|\lt 3 \)

C.\( |x-3|\lt 4 \)

D.\( |x-4|\lt 5 \)

Rozwiązaniem nierówności \(|x-2|\lt 5\) jest zbiór

A.\( (-3,7) \)

B.\( (-\infty , 3)\cup (7,+\infty) \)

C.\( (3,7) \)

D.\( (-\infty , -3)\cup (7,+\infty) \)

Wskaż nierówność, którą spełnia liczba \(\pi \)

A.\( |x+1|>5 \)

B.\( |x-1|\lt 2 \)

C.\( \left |x+\frac{2}{3} \right |\le 4 \)

D.\( \left |x-\frac{1}{3} \right |\ge 3 \)

Suma przedziałów \( (-\infty ,-11)\cup (7,+\infty) \) jest zbiorem rozwiązań nierówności:

A.\(|x+1|>10 \)

B.\(|x+2|>9 \)

C.\(|x-2|>11 \)

D.\(|x+1|\lt 10 \)

Zbiorem rozwiązań nierówności \( |x-2| > 7 \) jest przedział:

A.\((2,9) \)

B.\((-5,9) \)

C.\((-\infty,-5)\cup(9,+\infty) \)

D.\(( -\infty,-5 \rangle\cup\langle 9,+\infty ) \)

Najmniejszą liczbą całkowitą dodatnią spełniającą nierówność \(|x+4{,}5|\ge 6\) jest

A.\( x=1 \)

B.\( x=2 \)

C.\( x=3 \)

D.\( x=6 \)