Zbiór zadań - graniastosłupy i ostrosłupy - objętości i pola
Zbiór zadań do kursu: Matura podstawowa od 2023.
Dane są graniastosłup i ostrosłup o takich samych podstawach. Liczba wszystkich wierzchołków tego graniastosłupa jest o \(9\) większa od liczby wszystkich wierzchołków tego ostrosłupa. Podstawą każdej z tych brył jest
A.dziewięciokąt.
B.ośmiokąt.
C.osiemnastokąt.
D.dzicsięciokąt.
Dany jest ostrosłup prawidłowy trójkątny \(ABCS\) o podstawie \(ABC\). Punkty \(D\), \(E\) i \(F\) są środkami - odpowiednio - krawędzi bocznych \(AS\), \(BS\) i \(CS\) (zobacz rysunek).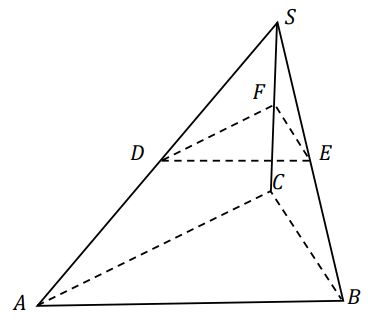 
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Stosunek objętości ostrosłupa \(DEFS\) do objętości ostrosłupa \(ABCS\) jest równy A.\( 3:4 \)
B.\( 1:4 \)
C.\( 1:8 \)
D.\( 3:8 \)
Suma liczby krawędzi i liczby wierzchołków ostrosłupa jest równa \(2020\). W podstawie tego ostrosłupa jest wielokąt o
A.\(505\) krawędziach.
B.\(673\) krawędziach.
C.\(721\) krawędziach
D.\(1010\) krawędziach
Podstawą ostrosłupa prawidłowego czworokątnego \(ABCDS\) jest kwadrat \(ABCD\). Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta \(ASC\) jest równa
A.\( 45^\circ \)
B.\( 30^\circ \)
C.\( 75^\circ \)
D.\( 90^\circ \)
Ze zbioru wszystkich krawędzi (krawędzi bocznych i krawędzi podstawy) ostrosłupa prawidłowego pięciokątnego losujemy jedną krawędź, a następnie z pozostałych krawędzi losujemy drugą. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowane krawędzie będą miały wspólny wierzchołek.
Różnica liczby krawędzi i liczby wierzchołków ostrosłupa jest równa \(11\). Podstawą tego ostrosłupa jest
A.dziesięciokąt.
B.jedenastokąt.
C.dwunastokąt.
D.trzynastokąt.
Podstawą ostrosłupa jest kwadrat \(KLMN\) o boku długości \(4\). Wysokością tego ostrosłupa jest krawędź \(NS\), a jej długość też jest równa \(4\) (zobacz rysunek).
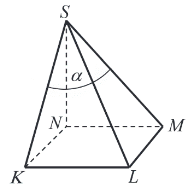Kąt \(α\), jaki tworzą krawędzie \(KS\) i \(MS\), spełnia warunek A.\( \alpha = 45^\circ \)
B.\( 45^\circ\lt \alpha \lt 60^\circ \)
C.\( \alpha\gt 60^\circ \)
D.\( \alpha = 60^\circ \)
Podstawą ostrosłupa prawidłowego czworokątnego \(ABCDS\) jest kwadrat \(ABCD\) (zobacz rysunek). Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta \(SAC\) jest równa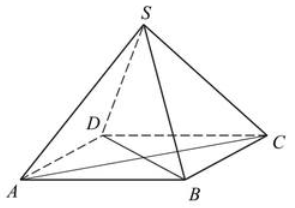 
A.\( 60^\circ \)
B.\( 45^\circ \)
C.\( 90^\circ \)
D.\( 75^\circ \)
Dany jest ostrosłup prawidłowy czworokątny, którego wysokość ma długość \(H\) oraz kąt między krawędzią boczną i płaszczyzną podstawy jest równy \(60^\circ \). Wyznacz wzór na pole powierzchni bocznej tego ostrosłupa w zależności od wysokości \(H\).
Trójkąt równoboczny \(ABC\) jest podstawą ostrosłupa prawidłowego \(ABCS\), w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem \(60^\circ \), a krawędź boczna ma długość \(7\) (zobacz rysunek). Oblicz objętość tego ostrosłupa. 
W graniastosłupie prawidłowym czworokątnym \(ABCDEFGH\) przekątna \(AC\) podstawy ma długość \(4\). Kąt \(ACE\) jest równy \(60^\circ\). Oblicz objętość ostrosłupa \(ABCDE\) przedstawionego na poniższym rysunku.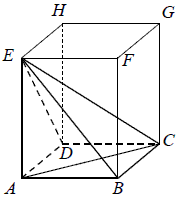 
W ostrosłupie prawidłowym trójkątnym \(ABCS\) krawędź podstawy ma długość \(a\). Pole powierzchni bocznej tego ostrosłupa jest dwa razy większe od pola jego podstawy. Oblicz cosinus kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny jego podstawy. 
W ostrosłupie prawidłowym trójkątnym krawędź boczna jest trzy razy dłuższa od wysokości ostrosłupa. Krawędź podstawy ma długość \(12\). Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.
Podstawą ostrosłupa \(ABCDS\) jest prostokąt o polu równym \(432\), a stosunek długości boków tego prostokąta jest równy \(3:4\). Przekątne podstawy \(ABCD\) przecinają się w punkcie \(O\). Odcinek \(SO\) jest wysokością ostrosłupa (zobacz rysunek). Kąt \(SAO\) ma miarę \(60^\circ \). Oblicz objętość tego ostrosłupa.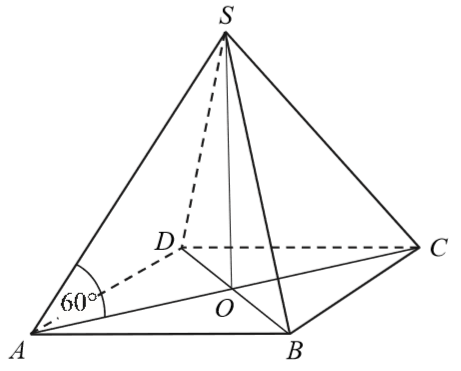 
Podstawą graniastosłupa \(ABCDEFGH\) jest prostokąt \(ABCD\) (zobacz rysunek), którego krótszy bok ma długość \(3\). Przekątna prostokąta \(ABCD\) tworzy z jego dłuższym bokiem kąt \(30^\circ\). Przekątna \(HB\) graniastosłupa tworzy z płaszczyzną jego podstawy kąt \(60^\circ\). Oblicz objętość tego graniastosłupa.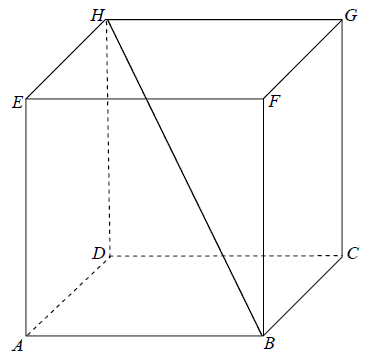 
Długość krawędzi bocznej ostrosłupa prawidłowego czworokątnego \(ABCDS\) jest równa \(12\). (zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt \(\alpha \) taki, że \(\operatorname{tg} \alpha =\frac{2}{\sqrt{5}}\). Oblicz objętość tego ostrosłupa.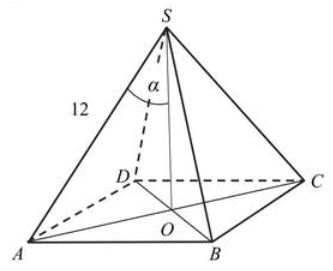 
Podstawą ostrosłupa \(ABCDE\) jest kwadrat, a spodek \(F\) wysokości \(EF\) ostrosłupa jest środkiem krawędzi \(AD\) (patrz rysunek). Ponadto wiadomo, że każda z dwóch dłuższych krawędzi bocznych tego ostrosłupa ma długość \(12\sqrt{5}\) cm i jest nachylona do płaszczyzny podstawy pod kątem \(60^\circ \). Oblicz objętość tego ostrosłupa.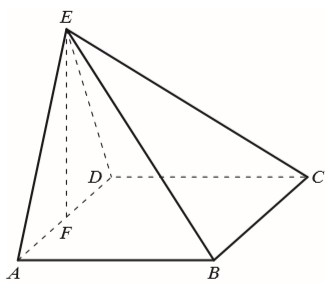 
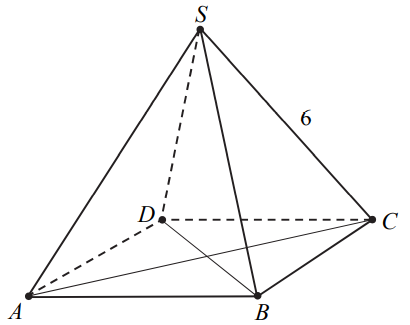
Dany jest ostrosłup prawidłowy czworokątny \(ABCDS\), którego krawędź boczna ma długość \(6\) (zobacz rysunek). Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy \(\sqrt{7}\). Oblicz objętość tego ostrosłupa. 