Matura podstawowa - kurs - część 55 - zadania

Wysokość graniastosłupa prawidłowego czworokątnego jest równa \(6\), a kąt nachylenia jego przekątnej do płaszczyzny podstawy jest równy \(60^\circ \). Długość tej przekątnej jest równa

W ostrosłupie prawidłowym czworokątnym \(ABCDS\) o podstawie \(ABCD\) i wierzchołku \(S\) trójkąt \(ACS\) jest równoboczny i ma bok długości \(8\). Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa (zobacz rysunek).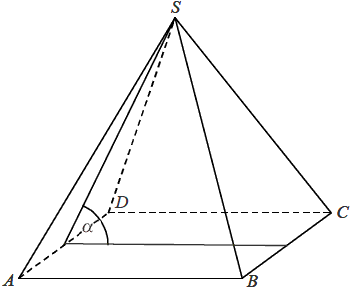

W graniastosłupie prawidłowym czworokątnym \(ABCDEFGH\) przekątna \(AC\) podstawy ma długość \(4\). Kąt \(ACE\) jest równy \(60^\circ\). Oblicz objętość ostrosłupa \(ABCDE\) przedstawionego na poniższym rysunku.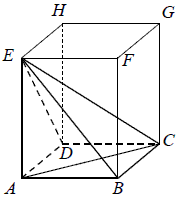

W ostrosłupie prawidłowym czworokątnym krawędź boczna ma długość \(5\) cm, a krawędź podstawy \(\sqrt{8}\) cm. Wówczas cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy jest równy:

W graniastosłupie prawidłowym czworokątnym wysokość graniastosłupa jest o \(4\) krótsza od przekątnej podstawy i o \(8\) krótsza od przekątnej graniastosłupa. Oblicz sinus kąta pomiędzy przekątną graniastosłupa a płaszczyzną podstawy.

W graniastosłupie prawidłowym czworokątnym \( ABCDEFGH \) połączono punkty będące środkami krawędzi \( BC \), \( CD \), \( AD \) i \( GH \). Wyznacz objętość powstałej bryły wiedząc, że \( \vert{DB}\vert=5\sqrt{2} \) i kąt \( DBH \) ma miarę \( 60^\circ \).

W graniastosłupie prawidłowym czworokątnym \(EFGHIJKL\) wierzchołki \(E, G, L\) połączono odcinkami (tak jak na rysunku). 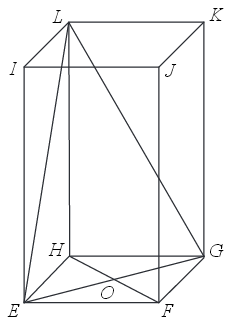Wskaż kąt między wysokością \(OL\) trójkąta \(EGL\) i płaszczyzną podstawy tego graniastosłupa.

Wysokość graniastosłupa prawidłowego czworokątnego jest równa \(16\). Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego cosinus jest równy \(\frac{3}{5}\). Oblicz pole powierzchni całkowitej tego graniastosłupa.

Pole podstawy graniastosłupa prawidłowego czworokątnego jest równe \(36\), a miara kąta nachylenia przekątnej graniastosłupa do płaszczyzny jego podstawy jest równa \(30^\circ\). Wysokość tego graniastosłupa jest równa

Krawędź boczna ostrosłupa prawidłowego trójkątnego jest nachylona do płaszczyzny podstawy pod kątem \(60^\circ\). Odległość spodka wysokości ostrosłupa od krawędzi bocznej jest równa \(4\). Oblicz objętość tego ostrosłupa.

Objętość ostrosłupa prawidłowego trójkątnego \(ABCS\) (tak jak na rysunku) jest równa \(72\), a promień okręgu wpisanego w podstawę \(ABC\) tego ostrosłupa jest równy \(2\). Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną.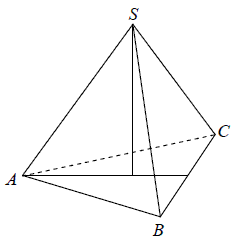

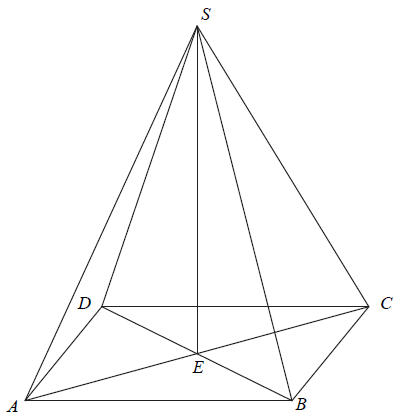
Podstawą ostrosłupa \(ABCDS\) jest kwadrat \(ABCD\). Wysokość \(SE\) ściany bocznej \(ADS\) jest jednocześnie wysokością ostrosłupa, a punkt \(E\) jest środkiem krawędzi \(AD\) (zobacz rysunek). Pole ściany \(ADS\) jest równe \(12\) cm², a objętość ostrosłupa jest równa \(48\) cm³. Oblicz miarę kąta nachylenia krawędzi bocznej \(CS\) do płaszczyzny podstawy ostrosłupa. Wynik zaokrąglij do \(1^\circ \).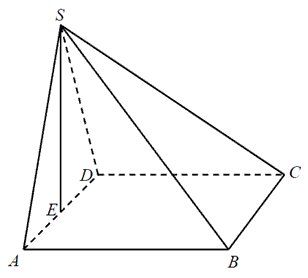

Podstawą ostrosłupa \(ABCDS\) jest romb \(ABCD\) o boku długości \(4\). Kąt \(ABC\) rombu ma miarę \(120^\circ \) oraz \(|AS|=|CS|=10\) i \(|BS|=|DS|\). Oblicz sinus kąta nachylenia krawędzi \(BS\) do płaszczyzny podstawy ostrosłupa.

Podstawą ostrosłupa \(ABCDS\) jest prostokąt, którego boki pozostają w stosunku \(3 : 4\), a pole jest równe \(192\) (zobacz rysunek). Punkt \(E\) jest wyznaczony przez przecinające się przekątne podstawy, a odcinek \(SE\) jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem \(30^\circ\). Oblicz objętość ostrosłupa.